|
||||||||||||||||||||||||
ГОСТ Р 50779.74-99
(ИСО 3951-89)
ГОСУДАРСТВЕННЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы
ПРОЦЕДУРЫ ВЫБОРОЧНОГО
КОНТРОЛЯ И КАРТЫ КОНТРОЛЯ
ПО КОЛИЧЕСТВЕННОМУ ПРИЗНАКУ
ДЛЯ ПРОЦЕНТА НЕСООТВЕТСТВУЮЩИХ
ЕДИНИЦ ПРОДУКЦИИ
ГОССТАНДАРТ РОССИИ
Москва
Предисловие
1 РАЗРАБОТАН И ВНЕСЕН Техническим комитетом по стандартизации ТК 125 «Статистические методы в управлении качеством продукции»;
АО «Научно-исследовательский центр контроля и диагностики технических систем» (АО «НИЦ КД»)
2 ПРИНЯТ И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Госстандарта России от 28 декабря 1999 г. № 774-ст
3 Настоящий стандарт, за исключением приложения Е, представляет собой аутентичный текст международного стандарта ИСО 3951-89 «Процедуры выборочного контроля и карты контроля по количественному признаку для процента несоответствующих единиц продукции»
4 ВВЕДЕН ВПЕРВЫЕ
СОДЕРЖАНИЕ
Введение
Настоящий стандарт устанавливает систему выборочного контроля на основе объема партии, приемлемого уровня качества AQL и уровней контроля. Стандарт применяют для контроля показателей качества продукции, измеряемых в непрерывной шкале и имеющих нормальное распределение или близкое к нему. Партия считается неприемлемой, если для распределения показателя качества продукции оценки среднего и изменчивости (дисперсии) не отвечают критериям приемки с заданными двусторонними допусками с отдельным уровнем качества и общим уровнем качества. В настоящем стандарте приведены числовой и графический критерии приемки. Процедуры выборочного контроля рассчитаны для случаев с известным и неизвестным стандартным отклонением.
В стандарте содержатся рекомендации по выбору между альтернативным и количественным признаком для статистического контроля, при этом наиболее важные параметры продукции контролируются по количественному признаку.
Данный стандарт рассчитан на контроль непрерывной серии партий, поступающей от одного источника, и достаточно большой для возможности применения правил переключения.
ГОСТ Р 50779.74-99
(ИСО 3951-89)
ГОСУДАРСТВЕННЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы
ПРОЦЕДУРЫ ВЫБОРОЧНОГО
КОНТРОЛЯ И КАРТЫ КОНТРОЛЯ
ПО КОЛИЧЕСТВЕННОМУ ПРИЗНАКУ ДЛЯ ПРОЦЕНТА НЕСООТВЕТСТВУЮЩИХ ЕДИНИЦ ПРОДУКЦИИ
Statistical methods. Sampling procedures and charts for inspection
by variables for percent nonconforming
Дата введения 2000-07-01
Глава I ОСНОВНЫЕ ПОЛОЖЕНИЯ
1 Цель и область применения
1.1 Цель
1.1.1 Настоящий стандарт устанавливает планы и процедуры выборочного контроля по количественному признаку. Настоящий стандарт применяют совместно с ГОСТ Р 50779.71.
1.1.2 Цель данного стандарта - обеспечение высокой вероятности приемки партий допустимого качества при максимально возможной вероятности отклонения партии недопустимого качества.
1.1.3 В настоящем стандарте для характеристики качества вышеназванных партий и процесса производства используется понятие «процент несоответствующих единиц продукции».
Настоящий стандарт применим в первую очередь для случаев:
a) когда процедура контроля предназначена для непрерывной последовательности партий дискретной продукции, которая целиком поставляется одним поставщиком, использующим один и тот же производственный процесс. При наличии разных поставщиков данные положения настоящего стандарта применимы к каждому из них в отдельности;
b) когда рассматривается только одна характеристика качества х этой продукции, которая должна измеряться с помощью непрерывной шкалы. Если важны несколько таких характеристик, то положения стандарта должны применяться к каждой из них;
c) когда в условиях стабильного производства (в состоянии статистической управляемости) характеристика качества х имеет нормальное распределение или близкое к нормальному распределению;
d) когда договором определяется верхний U или нижний L предел поля допуска или оба предела, а продукция оценивается как несоответствующая, если измеряемая характеристика х этой продукции удовлетворяет одному из приведенных ниже неравенств:
х>U, (1)
х<L, (2)
х>U или x<L. (3)
Неравенства (1) и (2) относятся к случаям с односторонним допуском, а неравенство (3) - к случаю с двусторонним допуском. Выбор между односторонним и двусторонним допусками делается в зависимости от того, применяется ли AQL к каждой границе в отдельности или применяется общий AQL к обеим границам (раздел 4).
2 Нормативные ссылки
В настоящем стандарте использованы ссылки на следующие стандарты:
ГОСТ Р 50779.11-2000 (ИСО 3534.2-93) Статистические методы. Словарь и условные обозначения. Часть 2. Статистическое управление качеством
ГОСТ Р 50779.21-96 Статистические методы. Правила определения и методы расчета статистических характеристик по выборочным данным. Часть 1. Нормальное распределение
ГОСТ Р 50779.30-95 Статистические методы. Приемочный контроль качества. Общие требования
ГОСТ Р 50779.42-98 (ИСО 8258-91) Статистические методы. Контрольные карты Шухарта
ГОСТ Р 50779.50-95 Статистические методы. Приемочный контроль качества по количественному признаку. Общие требования
ГОСТ Р 50779.53-98 Статистические методы. Приемочный контроль качества по количественному признаку для нормального закона распределения. Часть 1. Стандартное отклонение известно
ГОСТ Р 50779.71-99 (ИСО 2859.1-89) Статистические методы. Процедуры выборочного контроля по альтернативному признаку. Часть 1. Планы выборочного контроля последовательных партий на основе приемлемого уровня качества AQL
ГОСТ Р 50779.72-99 (ИСО 2859.2-85) Статистические методы. Процедуры выборочного контроля по количественному признаку. Часть 2. Планы выборочного контроля отдельных партий на основе предельного качества LQ
ИСО 2854-761) Статистическое представление данных. Методы оценки и проверки гипотез о средних значениях и дисперсиях
ИСО 5479-971) Статистическое представление данных. Критерий проверки отклонения от нормального распределения
ИСО 5725.2-941) Точность (истинность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерения
1) Оригиналы международных стандартов ИСО/МЭК - во ВНИИКИ Госстандарта России.
3 Определения и обозначения
3.1 Определения
В настоящем стандарте использованы термины с соответствующими определениями по ГОСТ Р 50779.11, ГОСТ Р 50779.71, а также приведенные ниже:
3.1.1 контроль по количественному признаку: Вид контроля, основанный на измерениях количественного показателя каждой единицы продукции из совокупности или выборки из нее.
3.1.2 приемочный выборочный контроль по количественному признаку: Процедура приемки, при которой приемлемость партии устанавливается статистически по результатам измерения определенного показателя единицы продукции из выборки.
3.1.3 приемлемый уровень качества (AQL): При контроле непрерывной последовательности партий - уровень качества, который при выборочном контроле служит допустимым пределом для среднего процента несоответствующих единиц продукции (раздел 4).
3.1.4 предельное качество: При контроле отдельной партии уровень качества при выборочном контроле ограничен нижним значением вероятности приемки (в настоящем стандарте: 10 % по 12.1).
3.1.5 несоответствие: Невыполнение установленного требования по показателю качества единицы продукции или услуги, оценка которого не зависит существенно от временного фактора.
Несоответствия, как правило, подразделяются по степени значимости на следующие классы:
класс А - наиболее значимые несоответствия. Применительно к приемочному выборочному контролю для этой группы несоответствий назначаются минимальные значения AQL;
класс В - менее значимые несоответствия. Для них могут назначаться большие значения AQL по сравнению с классом А и меньшие, чем для класса С (при наличии класса С) и т.д.
Количество классов и принципы отнесения несоответствий к классам должны отвечать требованиям каждого конкретного случая.
3.1.6 несоответствующая единица продукции: Единица продукции или услуга, имеющая хотя бы одно несоответствие.
3.1.7 s-метод: Метод оценки приемлемости партии на основе выборочного стандартного отклонения (раздел 14).
3.1.8 s-метод: Метод оценки приемлемости партии при условии, что известно стандартное отклонение процесса (раздел 15).
3.1.9 R-метод: Метод оценки приемлемости партии с помощью косвенного оценивания стандартного отклонения процесса, основанного на среднем размахе измерений единиц продукции в подгруппах выборки (приложение С).
3.1.10 предельное значение (предел поля допуска): Пограничное значение (верхнее, нижнее), установленное для количественного показателя качества продукции.
3.1.11 нижнее предельное значение (L): Предел, определяющий нижнюю предельную границу индивидуального значения показателя качества в процессе изготовления или оказания услуг.
3.1.12 верхнее предельное значение (U): Предел, определяющий верхнюю предельную границу индивидуального значения показателя качества в процессе производства или оказания услуг.
3.1.13 одностороннее предельное значение: Этот термин используется только в случаях указания одного предела поля допуска (далее - односторонний допуск).
3.1.14 предельные значения с отдельными уровнями качества: Этот термин используется в случае, когда указаны как нижний, так и верхний пределы, и значения AQL определены для каждого предела по 4.3 (далее - двусторонний допуск с отдельными уровнями качества).
3.1.15 предельные значения с общим уровнем качества: Данный термин используется, если установлены оба предельных значения и AQL определен для общего процента несоответствующих единиц по 4.3 (далее - двусторонний допуск с общим уровнем качества).
3.1.16 контрольный норматив (k): Константа, зависящая от установленного значения приемлемого уровня качества и объема выборки (14.2, 15.2 или С.5 приложения С).
3.1.17 статистика качества (Q): Функция пределов поля допуска, выборочного среднего и стандартного отклонения. Партия оценивается по результатам сравнения Q с контрольным нормативом k (14.2, 15.2 или С.5 приложения С).
3.1.18 нижняя статистика качества (QL): Функция нижнего предела поля допуска, выборочного среднего и стандартного отклонения. Партия оценивается по результатам сравнения QL с контрольным нормативом k (14.2, 15.2 или С.5 приложения С).
3.1.19 верхняя статистика качества (QU): Функция верхнего предела поля допуска, выборочного среднего и стандартного отклонения. Партия оценивается по результатам сравнения QU с контрольным нормативом k (14.2, 15.2 или С.5 приложения С).
3.1.20 максимальное выборочное стандартное отклонение (MSSD): В данном случае это наибольшее допустимое выборочное стандартное отклонение (14.6, В.8.3 приложения В).
3.1.21 максимальное стандартное отклонение процесса (MSSD): В данном случае наибольшее допустимое стандартное отклонение процесса (15.3, В.5.2 приложения В).
3.1.22 правила переключения: Правила перехода от одного плана контроля к другому в рамках схемы контроля, основанные на истории качества (раздел 19).
3.2 Обозначения
В данном стандарте использованы следующие обозначения:
fs - коэффициент из таблицы IVs, устанавливающий зависимость между максимальным выборочным стандартным отклонением и разностью U и L;
fs - коэффициент из таблицы IVs, устанавливающий зависимость между максимальным стандартным отклонением процесса и разностью U и L;
k - контрольный норматив при использовании s-, s- и R-методов;
К- контрольный норматив при известных m и s;
L - нижнее предельное значение;
U- верхнее предельное значение;
n - объем выборки;
N - объем партии;
Ра - вероятность приемки;
Q - статистика качества;
QL - нижняя статистика качества;
QU - верхняя статистика качества;
s - выборочное стандартное отклонение (оценка стандартного отклонения процесса), рассчитываемое по формуле
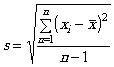
(символы см. в приложении А);
х - измеряемое значение показателя в выборке;
![]() - среднее
арифметическое значение х в выборке из п единиц (далее -
среднее);
- среднее
арифметическое значение х в выборке из п единиц (далее -
среднее);
![]() - нижнее приемочное значение;
- нижнее приемочное значение;
![]() - верхнее
приемочное значение;
- верхнее
приемочное значение;
m - среднее процесса;
s - стандартное отклонение процесса (s2 - квадрат стандартного отклонения, называемый дисперсией);
S - «сумма» (например, Sх - сумма значений х) чего-либо;
![]() - сумма значений
х„ когда i принимает значения от 1 до п;
- сумма значений
х„ когда i принимает значения от 1 до п;
> - «больше» (в частности, а>b означает, что а больше b),
³ - «больше или равно» (в частности, a³b означает, что а больше или равно b);
< - «меньше» (в частности, а<b означает, что а меньше b),
£ - «меньше или равно» (в частности, а£b означает, что а меньше или равно b).
4 Приемлемый уровень качества
4.1 Определение
При контроле непрерывной последовательности партий это уровень качества, который при выборочном контроле служит границей удовлетворительного среднего процента несоответствующих единиц продукции процесса.
4.2 Применение
AQL вместе с кодом объема выборки применяют для установления планов выборочной: контроля в данном стандарте.
Для двусторонних допусков возможны два способа задания AQL:
первый - для каждого предела задается отдельный AQL (в этом случае пределы поля допуске называются «предельными значениями с отдельными уровнями качества»);
второй - задается общий AQL для обоих пределов (в этом случае пределы поля допуск называются «предельными значениями с общим уровнем качества»).
4.4 Рекомендуемые значения AQL
В настоящем стандарте установлены одиннадцать рекомендуемых значений AQL в интервале от 0,1 % до 10 %. Для других значений AQL настоящий стандарт применять не следует (12.2).
Кроме того, заданы еще два значения AQL, равные 0,065 % и 15 %, необходимые для работы с правилами переключения (разделы 19 и 21). Планы и кривые приемки, соответствующие значениям AQL 0,065 % и 15 %, рекомендуется использовать только тогда, когда AQL при нормальном контроле принимает значения 0,1 % и 10 % соответственно и когда применяют правила переключения.
4.5 Предупреждение
Из определения AQL следует, что необходимый результат может быть получен только в том случае, если на контроль поступает непрерывная последовательность партий.
4.6 Ограничение
Назначение AQL не означает, что поставщик имеет право поставлять заведомо некачественную продукцию.
5 Правила переключения при нормальном, усиленном и ослабленном контроле
5.1 Для того, чтобы удержать поставщика от применения процессов со средним процентов несоответствующих единиц продукции выше AQL, предусмотрен переход к усиленному контролю при условии, что по результатам контроля среднее процесса действительно выше AQL; предусмотрено полное прекращение контроля, если через некоторое время усиленный контроль не будет способствовать улучшению производственного процесса.
5.2 Для достижения необходимого эффекта от использования AQL следует сочетать усиленный контроль и правила его прекращения в соответствии с настоящим стандартом.
5.3 Настоящий стандарт обеспечивает возможность переключения на ослабленный контроль если по результатам контроля средний процент несоответствующих единиц продукции стабилен и не выше AQL. Однако данная практика не является обязательной и выносится на усмотрение уполномоченной стороны.
5.4 Если контрольные карты показывают, что изменчивость процесса статистически управляема (по ГОСТ Р 50779.42), следует рассмотреть возможность переключения на s-метод. Если это приведет к положительному результату, то в дальнейшем за значение s можно принять s.
5.5 Если возникает необходимость в прекращении контроля, он не может быть возобновлен до тех пор, пока поставщик не предпримет мер, направленных на улучшение качества поставляемой продукции.
5.6 Более подробно принципы работы с правилами переключения изложены в разделах 19 и 20.
6 Взаимосвязь с ГОСТ Р 50779.71
6.1 Сходство
a) Настоящий стандарт является дополнением к ГОСТ Р 50779.71. Оба эти стандарта имеют общую концепцию, общие процедуры и максимально приближенные термины и определения.
b) В обоих стандартах AQL является характеристикой выборочных планов и рекомендуемые значения AQL данного стандарта (а именно от 0,1 % до 10 %) те же, что и по ГОСТ Р 50779.71.
c) В обоих стандартах по объему партии и уровню контроля (при отсутствии других рекомендаций предпочтителен уровень контроля II) определяют условный код. Затем по коду и AQL в соответствии с выбранным методом (s-метод, s-метод или, при определенных условиях, R-метод) из таблиц получают объем выборки и критерии приемки. Для каждого вида контроля: нормального, усиленного и ослабленного существуют отдельные таблицы.
d) Правила переключения в основном совпадают.
e) Классификация несоответствий по степени значимости по классам А, В и т.д. совпадает.
6.2 Отличие
a) Определение приемлемости
Приемлемость партии по альтернативному признаку в ГОСТ Р 50779.71 определяется числом несоответствующих единиц продукции, обнаруженных в выборке. Критерий приемлемости при контроле по количественному признаку основан на оценке мер расположения и изменчивости распределения измеряемого параметра единицы продукции в партии относительно пределов поля допуска. В настоящем стандарте представлены два метода: s-метод для случаев, когда неизвестно стандартное отклонение, и s-метод, если значение s известно. Третий метод, R-метод, изложен в приложении С. В случаях одностороннего или двустороннего допуска критерии приемлемости могут быть рассчитаны по формулам, приведенным в 14.2 и 15.2, но быстрее их найти графически по 14.3. Для пределов двустороннего допуска с общим AQL данный стандарт устанавливает графический метод по 14.6 и 15.3.
b) Нормальность
ГОСТ Р 50779.71 не задает требований к распределению характеристик. В соответствии с настоящим стандартом в целях применения более эффективного плана контроля предполагается, что измерения распределяются по нормальному закону или по закону, близкому к нормальному.
c) Оперативные характеристики
В то время, как для плана контроля по альтернативному признаку можно подобрать план контроля по количественному признаку с близкой оперативной характеристикой, в то же время невозможно добиться совпадения всех оперативных характеристик, соответствующих одному и тому же коду и AQL, без увеличения объема выборки. Для s-метода объем выборки сохраняется неизменным для данного объема партии во всем диапазоне значений AQL; для s-метода это ограничение снимается, чтобы приблизить оперативные характеристики как для AQL, так и для предельного качества.
d) Вероятность приемки при AQL
Вероятность того, что партия качеством, точно соответствующим AQL, будет принята, возрастает по мере увеличения объема выборки и ведет себя приблизительно так же, как и в ГОСТ Р 50779.71.
e) Объемы выборок
Для одного и того же кода объем выборки при контроле по количественному признаку обычно меньше, чем при контроле по альтернативному признаку.
f) Планы двуступенчатого выборочного контроля
Эти планы в настоящем стандарте не приводятся.
g) Предел среднего выходного качества (AOQL)
Концепция AOQL не применима в условиях разрушающего или дорогостоящего контроля и испытаний, при которых невозможны сплошной контроль и разбраковка непринятых партий. Хотя планы контроля по количественному признаку могут использоваться в этих условиях, настоящий стандарт не включает таблицы AOQL.
7 Мелкосерийное производство и оперативные характеристики
7.1 Мелкосерийное производство
a) Схемы выборочного контроля настоящего стандарта не предназначены для условий, отличных от указанных в 1.2, например, для отдельной партии или небольшого числа партий, где не применяют усиленный контроль и правила прекращения контроля.
b) В условиях мелкосерийного производства концепция AQL не применима, так как в центре внимания потребителя оказывается качество ограниченного числа поставляемых партий, и ему нет необходимости прикладывать усилия к управлению качеством самого процесса. Но AQL все еще будет характеристикой качества поставляемой продукции, имеющей высокую вероятность приемки, и поэтому может быть использован при выборе планов контроля (раздел 12).
7.2 Оперативные характеристики
a) О степени защиты потребителя, обеспечиваемой определенным планом выборочного контроля по настоящему стандарту, можно судить по оперативным характеристикам ОХ, приведенным в таблицах VB и таблицах от VB-1 до VP-1, которые также следует использовать при выборе планов выборочного контроля.
b) Оперативные характеристики предназначены для нормального контроля, применяющего s-метод с односторонним допуском, но они дают достаточно хорошее приближение и для двустороннего допуска с общим AQL.
c) Оперативные характеристики, соответствующие одинаковому коду и AQL, обеспечивают хорошее приближение при использовании s-метода (и R-метода) в случае небольшого объема выборки
d) В настоящем стандарте отсутствуют некоторые оперативные характеристики для усиленного и ослабленного контроля, однако, их можно взять из числа оперативных характеристик, предназначенных для нормального контроля (таблицы VIA и VIB).
Глава II ВЫБОР ПЛАНА КОНТРОЛЯ
8 Планирование
Для выбора подходящего плана контроля по количественному признаку, при его наличии, требуются опыт, здравый смысл, знание статистических методов и контролируемой продукции. Этот раздел настоящего стандарта содержит основные положения, которыми следует руководствоваться, выбирая план контроля по количественному признаку в качестве требуемого стандартного плана.
9 Выбор между планами по количественному и альтернативному признакам
Вначале решается вопрос о выборе метода контроля - по количественному признаку или по альтернативному признаку. Здесь необходимо учесть следующее:
a) с точки зрения экономики необходимо сравнить общие затраты на сравнительно простую схему контроля большого числа изделий по альтернативному признаку с затратами на схему контроля по количественному признаку, которая обычно более трудоемка и требует больших временных и финансовых затрат в расчете на единицу продукции;
b) с точки зрения информативности предпочтение отдается контролю по количественному признаку, так как он позволяет собрать более полную информацию о качестве продукции и раньше предупреждает об ухудшении качества;
c) схема контроля по альтернативному признаку может быть более доступна для понимания, тогда как при контроле по количественному признаку трудно понять тот факт, что партия может отклоняться по результатам измерений, хотя в выборке нет ни одной несоответствующей единицы (пример по 14.6);
d) в таблице IB сравниваются объемы выборок, необходимые для одного и того же AQL согласно типовому плану контроля по альтернативному признаку (ГОСТ Р 50779.71), и типовые планы настоящего стандарта. Из них видно, что s-метод для случаев с известным стандартным отклонением требует минимального объема выборок;
e) контроль по количественному признаку особенно эффективен при использовании соответствующих контрольных карт;
i) контроль по количественному признаку имеет существенное преимущество в тех случаях, когда процесс контроля дорогостоящий, в частности, при разрушающем контроле;
g) схема контроля по количественному признаку теряет свое преимущество по мере того, как растет количество измерений на каждое изделие, поскольку каждый показатель качества должен рассматриваться отдельно. В этом случае проводят контроль по альтернативному признаку. Для большинства характеристик имеет смысл контролировать по количественному признаку один или два наиболее важных показателя качества. Например, при проведении испытаний на нагрузку по количественному признаку контролируются показатели безопасности и надежности;
h) настоящий стандарт применим только для случая с нормальным законом распределения. Если есть сомнение, следует посоветоваться с уполномоченной стороной (лицом, организацией).
Примечания
1 Критерии проверки отклонения от нормального распределения рассматриваются в ГОСТ Р 50779.21 и разделе 2 ИСО 2854, где содержатся примеры графических методов, которыми можно пользоваться для проверки того факта, что распределение в достаточной степени близко к нормальному, чтобы подтвердить выбор метода контроля по количественному признаку.
2 В ИСО 5479 содержится более подробное исследование на нормальность.
10 Выбор метода
Если выбор сделан в пользу контроля по количественному признаку, возникает вопрос, касающийся того, какой метод должен использоваться: s-метод или s-метод (или R-метод).
s-метод наиболее выгоден экономически в части объема выборки, но прежде чем его применять необходимо установить значение s.
По объему выборки s-метод имеет небольшое преимущество перед R-методом, но для нахождения s требуется больший объем вычислений, что можно сделать при наличии электронного калькулятора. Методы вычисления s описаны в приложении А.
R-метод прост для вычислений, но требует большого объема выборки для одинаковых AQL (приложение С). Недостатком является то, что для объема выборки 10 и более приемлемость партии может зависеть от разбиения выборки на подгруппы.
Первоначально необходимо начать с контроля по s-методу (или R-методу), но если качество удовлетворительное, типовые правила переключения позволят уполномоченной стороне применить ослабленный контроль и брать меньшие объемы выборок.
Тогда встает вопрос, если изменчивость процесса находится в состоянии статистической управляемости и продолжается приемка партий, будет ли экономнее переключение на s-метод?
При s-методе объем выборки будет меньше и правила приемки упрощаются (15.2, 15.3), но с другой стороны необходимо вычислить s для регистрации результатов контроля и вести контрольные карты (по разделу 18).
11 Выбор уровня контроля и AQL
В типовых планах выборочного контроля уровень контроля в сочетании с объемом партий и AQL определяет объем выборки для контроля и степень его жесткости. Соответствующая кривая ОХ, представленная в одной из таблиц от VB до VP, свидетельствует о степени риска для такого плана.
Выбор уровня контроля и AQL зависит от множества факторов, но в большинстве случаев от соотношения между общей суммой затрат на контроль и последствий от эксплуатации несоответствующих изделий.
В обычной практике используют уровень контроля II, если отсутствуют особые обстоятельства в пользу другого уровня контроля.
12 Выбор плана контроля
Стандартные процедуры контроля применяют только в случаях непрерывного производства.
Опыт показывает, что с помощью стандартных пошаговых процедур: от объема партии к объему выборки с применением уровня контроля II, начиная с s-метода, можно получать приемлемые для работы планы, причем по степени важности на первом месте стоит такая характеристика, как AQL, затем - объем выборки п и, наконец, предельное качество LQ.
Приемлемость такой системы обусловлена тем, что потребитель защищен правилами переключения (по разделу 19), которые быстро увеличивают жесткость контроля и, в конечном итоге, прекращают приемку в случае, если качество процесса ниже AQL.
Примечание - Следует помнить, что предельное качество - это качество с 10 %-ной вероятностью приемки. Фактический риск потребителя поэтому зависит и от вероятности того, что изделия такого низкого качества будут предъявлены на контроль.
Если в определенных случаях предельное качество имеет более высокий приоритет, чем объем выборки (например, при изготовлении ограниченного числа партий), подходящий план может быть выбран с помощью диаграммы А настоящего стандарта. Точка пересечения вертикальной прямой, проходящей через точку «допустимое значение предельного качества», и горизонтальной прямой, проходящей через точку «требуемое качество, обеспечиваемое с 95%-ной вероятностью приемки» (приблизительно равное AQL), будет располагаться выше или на наклонной прямой с кодом объема выборки, соответствующей заданным требованиям. Это должно проверяться с помощью контроля оперативной характеристики из таблицы V для данного кода и AQL.
Если линии пересекаются в точке над линией с пометкой Р на диаграмме А, из этого следует, что для s-метода необходима выборка более 200 изделий и данные требования не соответствуют планам контроля настоящего стандарта.
12.2 Специальные планы
Если типовые планы неприемлемы, то должны быть выбраны специальные планы.
Необходимо выбрать наиболее подходящее сочетание AQL, предельного качества и объема выборки, имея в виду, что эти характеристики взаимозависимы, поскольку любые две из них определяют третью.
Примечание - Свобода выбора планов в известной мере ограничена; то обстоятельство, что объем выборки обязательно является целым числом, накладывает некоторые ограничения. Если необходима специальная схема, она должна строиться только под руководством специалиста по статистике, имеющего большой опыт работы в области статистического управления качеством.
Глава III РАБОТА С ПЛАНОМ ВЫБОРОЧНОГО КОНТРОЛЯ ПО КОЛИЧЕСТВЕННОМУ ПРИЗНАКУ
13 Предварительные действия
Перед началом контроля по количественному признаку необходимо проверить следующее:
a) является ли распределение вероятностей нормальным и производство непрерывным;
b) с какого метода s (или R) следует начать или, если стандартное отклонение известно и устойчиво, то в каком случае следует пользоваться s-методом;
c) был ли установлен уровень контроля. При его отсутствии применяют уровень контроля II;
d) установлен ли один из рекомендуемых настоящим стандартом AQL. В противном случае таблицы неприменимы;
e) если установлен двусторонний допуск, проверьте, определены ли AQL для каждого предела поля допуска или задан ли общий AQL.
14 Стандартная процедура для s-метода
14.1 Процедура получения плана
Процедура получения плана следующая:
a) по заданному уровню контроля (как правило, уровень II) и объему партии с помощью таблицы IA найдите код объема выборки;
b) с этим кодом и значением AQL из таблицы IIА получите объем выборки п и контрольный норматив k;
c) взяв случайную выборку этого объема,
измерьте показатель качества х каждой единицы, после чего вычислите ![]() (среднее выборки) и s (оценку стандартного отклонения), используя приложение А.
Если
(среднее выборки) и s (оценку стандартного отклонения), используя приложение А.
Если ![]() выходит за пределы
поля допуска, партия считается неприемлемой и без расчета s, но может понадобиться вычислить s для регистрации данных.
выходит за пределы
поля допуска, партия считается неприемлемой и без расчета s, но может понадобиться вычислить s для регистрации данных.
14.2 Критерии приемлемости для одностороннего и двустороннего допусков
Если заданы односторонний или двусторонний допуски, статистика качества вычисляется по формуле
![]()
и (или)
![]()
соответственно, после чего статистика качества QU и (или) QL сравнивается с контрольным нормативом k, полученным из таблицы IIA для нормального контроля.
Если соответствующая статистика больше или равна k, то партия принимается, в противном случае она отклоняется.
Таким образом, если указано только верхнее предельное значение поля допуска U, то партия:
принимается, если QU³k;
не принимается, если QU <k.
Или, если указано только нижнее предельное значение поля допуска L, то партия:
принимается, если QL³k;
не принимается, если QL<k.
Если заданы U и L (значения х различны, если даются разные AQL), то партия:
принимается, если Q³k и Q£kU;
не принимается, если выполняется хотя бы одно из условий QL<kL или Qv<kv.
Пример - Согласно техническим условиям на продукцию максимальная температура работы некоторого прибора не должна превышать 60°С. Контролируем партии продукции по 100 единиц. Выбираем уровень контроля II и применяем нормальный контроль с AQL=2,5 %.
Из таблицы IA находим код F. Из таблицы IIA видно, что требуемый размер выборки - 10 изделий, и контрольный норматив k равен 1,41. Предположим, что получены следующие измеренные значения температуры: 53°С; 57°С; 49°С; 58°С; 59°С; 54°С; 58°С; 56°С; 55°С; 50°С. Следует определить, соответствует ли партия критерию приемки.
Необходимая информация Полученные значения
Объем выборки: п 10
Среднее выборки ![]() 54,9
54,9
Стандартное отклонение s: ![]() 3,414
3,414
(по А.1.2 приложения А);
Верхнее предельное значение: U 60
QU=(U-![]() )s , 1,494
)s , 1,494
Контрольный норматив: k (по таблице IIА) 1,41
Критерии приемки: сравниваем QU c k 1,494>1,41
Данная партия удовлетворяет критерию приемки и, следовательно, принимается.
14.3 Графический метод для одностороннего допуска
Для использования графического метода необходимо построить прямую:
![]() =U - ks - для верхнего предельного значения или
=U - ks - для верхнего предельного значения или
![]() =L
+ ks - для нижнего предельного
значения с осями координат:
=L
+ ks - для нижнего предельного
значения с осями координат:
![]() - вертикальная ось, s - горизонтальная ось.
- вертикальная ось, s - горизонтальная ось.
При контроле по верхнему предельному
значению допуска зона приемки располагается под прямой. При контроле по нижнему
значению - эта зона лежит над прямой. Используя конкретные значения s и ![]() , рассчитанные на основе измерений в выборке (приложение А)
для нахождения s, необходимо нанести точку (s,
, рассчитанные на основе измерений в выборке (приложение А)
для нахождения s, необходимо нанести точку (s, ![]() ) на график. Если эта точка попадает в зону приемки, партия
должна быть принята, если выходит за ее границы, то партия отклоняется.
) на график. Если эта точка попадает в зону приемки, партия
должна быть принята, если выходит за ее границы, то партия отклоняется.
Пример - Используя данные примера по 14.2, отметьте точку U=60 на вертикальной оси и проведите прямую, проходящую
через эту точку с наклоном, соответствующим константе минус k, причем k=1,41.
Это означает, что прямая проходит через точки (s=1; ![]() =58,59), (s= 2;
=58,59), (s= 2; ![]() =57,18), (s=3;
=57,18), (s=3; ![]() =55,77). Выберите подходящую точку и проведите прямую линию
через нее и точку с координатами (s=0;
=55,77). Выберите подходящую точку и проведите прямую линию
через нее и точку с координатами (s=0; ![]() =60), то есть U.
Зона приемки находится под прямой. Выберите нужную точку с координатами (
=60), то есть U.
Зона приемки находится под прямой. Выберите нужную точку с координатами (![]() =54,9; s=3,414).
Как видно на рисунке
1, она расположена в зоне приемки, значит, партия принимается.
=54,9; s=3,414).
Как видно на рисунке
1, она расположена в зоне приемки, значит, партия принимается.
Такой график можно построить до начала
контроля серии партий. Далее для каждой партии нанесите точку (s; ![]() ) и решайте, может ли эта партия быть принята.
) и решайте, может ли эта партия быть принята.
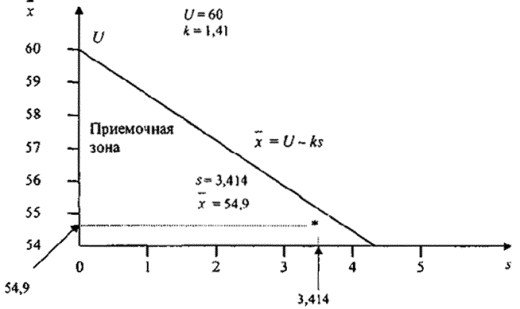
Рисунок 1 - Пример использования приемочной карты для одностороннего допуска (s-метод)
14.4 Числовой способ для одностороннего или двустороннего допуска
Пример - Пиротехническая задержка по времени должна составлять от 4 до 9 с.
Произведенная продукция контролируется партиями по 1000 изделий: уровень контроля II, нормальный контроль: AQL=0,1 % -для нижнего предела поля допуска и AQL=2,5 % -для верхнего предела. Из таблицы IA видно, что для такого размера партии код - J. Из таблицы IB видно, что для s-метода объем выборки равен 35 и по таблице IIА находим, что верхний и нижний контрольные нормативы равны kU=1,57 и kL - 2,54 соответственно.
Допустим, время задержки в выборке распределяется следующим образом:
6,95 6,04 6,68 6,63 6,65
6,40 6,44 6,34 6,04 6,15
6,44 7,15 6,70 6,59 6,51
6,35 7,17 6,83 6,25 6,96
6,80 5,84 6,15 6,25 6,57
6,52 6,59 6,86 6,57 6,91
6,29 6,63 6,70 6,67 6,67
Требуется определить соответствие критериям приемки.
Необходимая информация Полученные значения
Объем выборки: п 35
Среднее выборки ![]() 6,55
6,55
Стандартное отклонение s: ![]() 0,31
0,31
(по А.1.2 приложения А);
Верхнее предельное значение: U 9,0
QU=(U-![]() )/s 7,90
)/s 7,90
Контрольный норматив: kU (таблица IIА) 1,57
Нижнее предельное значение: L 4,0
QL=(![]() -L)/s 8,23
-L)/s 8,23
Контрольный норматив: kL (таблица IIА) 2,54
Критерий приемки равен: QU ³kU и QL³kL 7,90>1,57и 8,23>2,54
Данная партия отвечает критериям приемки и может быть принята.
14.5 Графический метод для двустороннего допуска
При использовании графического метода для двустороннего допуска необходимо построить следующие прямые
![]() =U-kUs
(для верхнего предела) или
=U-kUs
(для верхнего предела) или
![]() =L+kLs
(для нижнего предела)
=L+kLs
(для нижнего предела)
с осями координат: ![]() - вертикальная ось, s - горизонтальная ось. Используя конкретные значения
- вертикальная ось, s - горизонтальная ось. Используя конкретные значения ![]() и s, рассчитанные по измерениям в выборке, необходимо нанести
точку (
и s, рассчитанные по измерениям в выборке, необходимо нанести
точку (![]() , s) на
график. Если эта точка лежит в зоне приемки, то партия принимается, если она
выходит за границы этой зоны, то партия не принимается.
, s) на
график. Если эта точка лежит в зоне приемки, то партия принимается, если она
выходит за границы этой зоны, то партия не принимается.
Пример - Используя данные примера по 14.4, отметьте точку U=9 на вертикальной оси. Проведите через эту точку
прямую с наклоном, соответствующим коэффициенту минус k, причем kU=1,57. Это значит, что прямая пройдет и через точку (s=1; ![]() =7,43). Также отметьте точку L=4 на оси
=7,43). Также отметьте точку L=4 на оси ![]() и проведите прямую
через эту точку с наклоном, соответствующим коэффициенту плюс kL, причем kL=2,54. Это означает, что прямая пройдет через точку (s =1;
и проведите прямую
через эту точку с наклоном, соответствующим коэффициенту плюс kL, причем kL=2,54. Это означает, что прямая пройдет через точку (s =1; ![]() =6,54). Зона приемки соответствует зоне, ограниченной построенными
прямыми и осью
=6,54). Зона приемки соответствует зоне, ограниченной построенными
прямыми и осью ![]() . Рассчитанные значения s и
. Рассчитанные значения s и ![]() равны 0,31 и 6,55.
Нанесите точку (s=0,31;
равны 0,31 и 6,55.
Нанесите точку (s=0,31; ![]() =6,55). Как видно на рисунке 2, она лежит в пределах зоны приемки,
значит, партия принимается.
=6,55). Как видно на рисунке 2, она лежит в пределах зоны приемки,
значит, партия принимается.

Рисунок 2 - Пример использования приемочной карты для двустороннего допуска (s-метод)
14.6 Критерий приемки для предельных значений с общим уровнем качества
Если заданы предельные значения с общим уровнем качества, то необходимо использовать графический метод при условии, что s не превышает значения максимального стандартного отклонения выборки (MSSD) из таблицы IVs (в этом случае партия будет сразу же отклонена).
Из набора карт для s-метода, имеющих соответствующий код, необходимо выбрать кривую приемки с AQL, заданными для двух пределов поля допуска.
Затем вычисляют значения
![]() и
и
отмечают точку, соответствующую этим значениям на графике (или его копии). Если точка попадает в зону приемки, партию принимают, если нет, партию отклоняют.
Для удобства вычислений рекомендуется до
начала контроля скопировать приемочные кривые нормального и усиленного контроля
на графическую бумагу (лист со специальной графической бумагой, необходимой для
этого, представлен в приложении D).
Масштаб должен быть выбран так, чтобы верхней границе на оси ![]() соответствовало
значение 1, а нижней - 0.
соответствовало
значение 1, а нижней - 0.

Рисунок 3 - Кривая приемки для кода объема выборки F, AQL=1,5 %, MSSD=2,76 (s-метод)
Затем отмечают на карте значения s и
![]() , полученные на выборке. Если точка находится внутри зоны
приемки, партия принимается; если она находится вне этой зоны - партия
отклоняется.
, полученные на выборке. Если точка находится внутри зоны
приемки, партия принимается; если она находится вне этой зоны - партия
отклоняется.
Примечание - Для
выборок с кодом В и С (то есть для объемов выборок 3 и 4) зона приемки
ограничивается четырьмя прямыми: осью ![]() ; прямой
; прямой ![]() =U
- ks, прямой,
параллельной оси
=U
- ks, прямой,
параллельной оси ![]() и проходящей через MSSD (таблица IVs), и прямой
и проходящей через MSSD (таблица IVs), и прямой ![]() =L+ks. Значения величины k берут из таблиц IIA, IIB или IIС.
=L+ks. Значения величины k берут из таблиц IIA, IIB или IIС.
Пример - Для некоторого устройства установлены требования по температуре: минимум 60,0°С и максимум 70,0°С. Продукция контролируется партиями по 96 изделий. Уровень контроля II. Нормальный контроль с AQL=1,5 %. Из таблицы IА находим код объема выборки F. Из таблицы IB находим, что требуется объем выборки 10. Из таблицы IVs видно, что значение fs для MSSD равно 0,276. Предположим, что полученные измерения равны: 63,5°С; 62,0°С; 65,2°С; 61,7°С; 69,0°С; 67,1°С; 60,0°С; 66,4°С; 62,8°С; 68,0°С. Требуется найти соответствие критерию приемки.
Необходимая информация Полученные значения
Объем выборки: п 10
Среднее выборки ![]() 64,57
64,57
Стандартное отклонение s: ![]() 3,01
3,01
(по А.1.2 приложения А);
Значение fs - для MSSD (по таблице IVs ) 0,276
MSSD= fs(U-L) 2,76
Соответствующая кривая приемки берется из диаграммы s - F.
Если (см. рисунок 3) масштаб установлен по
реальным измерениям, то нанесите на нем точку (s=3,01; ![]() =64,57). Она лежит вне кривой приемки, значит, партия
отклоняется. Эта партия могла быть отклонена, как только стало ясно, что
значение s превышает MSSD.
=64,57). Она лежит вне кривой приемки, значит, партия
отклоняется. Эта партия могла быть отклонена, как только стало ясно, что
значение s превышает MSSD.
Если масштаб произвольный, необходимо
провести нормирование значений s и ![]() следующим образом:
следующим образом:
Нормированное среднее:
(![]() -L)/(U-L)=(64,57-60)/(70-60)=0,457.
-L)/(U-L)=(64,57-60)/(70-60)=0,457.
Нормированное стандартное отклонение: s/(U- L)=3,01/(70-60)=0,301.
Точка (0,301; 0,457) отмечается на рисунке 3.
Эта партия отклоняется, так как она выходит за границы кривой приемки для AQL=1,5 %.
15 Стандартная процедура для s-метода
15.1 Построение плана контроля
Этим методом следует пользоваться при наличии серьезных оснований считать стандартное отклонение процесса постоянным и равным s.
Из таблицы IА следует найти код, после чего для нормального контроля из таблицы IIIA по коду объема выборки и указанному AQL получаем объем выборки п и контрольный норматив k.
Далее следует взять случайную выборку
заданного объема, для каждой единицы продукции измерить значение характеристики
х и вычислить среднее ![]() .
.
15.2 Критерии приемки для одностороннего и двустороннего допусков
Критерий приемки можно получить, следуя процедуре, заданной для s-метода, подстановкой s (стандартное отклонение процесса) вместо s, полученного, по отдельным выборкам, и сравнивая вычисленные значения Q с контрольным нормативом k, полученным по таблице IIIА.
Причем, если QU=(U-![]() )/s, QU³kU, критерий приемки для верхнего предела имеет вид
)/s, QU³kU, критерий приемки для верхнего предела имеет вид ![]() £U-kUs.
£U-kUs.
Поскольку U, kU
и s известны заранее,
приемочное значение ![]() =U-kUs должно быть указано до начала контроля. После этого
критерий приемки для верхнего предела поля допуска принимает вид:
=U-kUs должно быть указано до начала контроля. После этого
критерий приемки для верхнего предела поля допуска принимает вид:
партия принимается, если ![]() £
£![]() (
(![]() =U-kUs);
=U-kUs);
партия не принимается, если ![]() >
>![]() (
(![]() =U-kUs).
=U-kUs).
Аналогично для нижнего предела поля допуска:
партия принимается, если ![]() ³
³![]() (
(![]() =L+kLs);
=L+kLs);
партия не принимается, если ![]() ³
³![]() (
(![]() =L+kLs).
=L+kLs).
Если указаны оба предела поля допуска, то:
партия принимается, если одновременно
выполняются условия ![]() £
£![]() или
или ![]() ³
³![]() ;
;
партия не принимается, если выполняется
одно из условий ![]() >
>![]() или
или ![]() ³
³![]() .
.
Пример - Минимальное значение точки текучести стального литья в соответствии с установленными требованиями составляет 400 Н/мм2. На контроль подается партия из 500 изделий. Должен применяться уровень контроля II, нормальный контроль с AQL=1,5 %. Известно, что s равна 21 Н/мм2. Из таблицы IA следует, что код выборки - I.
Из таблицы IIIA для AQL=1,5 % получаем объем выборки n, равный 10, и контрольный норматив, равный 1,70. Например, получены следующие значения:
431; 417; 469; 407; 452; 427; 421; 476; 400; 445.
Необходимо определить соответствие критерию приемки данной партии продукции.
Необходимая информация Полученные значения
Контрольный норматив: k 1,70
Известное s 21
Произведение: ks 35,70
Нижнее предельное значение: L 400
Приемочное значение: L+ks=![]() 435,70
435,70
Сумма измерений: Sx 4345
Объем выборки: n 10
Среднее выборки: ![]() 434,5
434,5
Критерий приемки: ![]() >
> ![]() Не
принимается
Не
принимается
Среднее выборки из партии не удовлетворяет критерию приемки, поэтому партия не принимается.
15.3 Критерий приемки для предельных значений с общим уровнем качества
Если заданы верхний и нижний предельные значения с общим уровнем качества, необходимо использовать графический метод (если значение s не выше MPSD, взятой из таблицы IVs, то партия сразу должна быть отклонена без взятия выборки).
Рекомендуется следующая процедура:
a) с учетом объема партии и заданного уровня контроля необходимо найти код по таблице IA и объем выборки по таблице IВ, используя код объема выборки и AQL;
b) из множества карт для разных кодов объема выборки необходимо выбрать кривую приемки для AQL, установленного для данного плана;
c) вычисляется значение s/(U-L) и через эту точку проводится вертикальная прямая;
d) если эта прямая пересекает кривую приемки,
вычисляются значения (![]() -L)/(U-L) в точках
пересечения. Они образуют верхние и нижние нормированные приемочные значения
выборочного среднего (рисунок
4).
-L)/(U-L) в точках
пересечения. Они образуют верхние и нижние нормированные приемочные значения
выборочного среднего (рисунок
4).
Приемочные значения ![]() и
и ![]() рассчитываются затем,
как показано ниже в примере.
рассчитываются затем,
как показано ниже в примере.
Примечания
1 Если эта прямая не пересекает кривую приемки, процесс недопустимый, и выборочный контроль теряет смысл,
2 Если эта прямая пересекает прямолинейные участки приемочной кривой, то это соответствует двустороннему допуску и критериям приемки по 15.2.
е) согласно 15.3, перечисление а), необходимо взять выборку нужного размера и рассчитать среднее значение контролируемого параметра;
f) критерий приемки заключается в следующем: если
среднее попадает между верхним и нижним приемочными значениями для ![]() (то есть, если
(то есть, если ![]() £
£![]() £
£![]() ), то партия
принимается, в других случаях - отклоняется.
), то партия
принимается, в других случаях - отклоняется.
Пример - Сопротивление некоторой электрической компоненты устанавливается техническими условиями из расчета (520±50) Ом. Объем партии составляет 2500 изделий. Уровень контроля II, нормальный, с одним и тем же AQL, равным 4 % для двустороннего допуска (470 и 570). Задано значение s, равное 21,0. Из таблицы IА находим код объема выборки К. Из таблицы IB находим требуемый объем выборки, равный 25. Пусть заданы следующие выборочные значения сопротивления:
515; 491; 479; 507; 543; 521; 536; 483; 509; 514; 507; 484; 526; 552; 499; 530; 512; 492; 521; 467; 489; 513; 535; 501; 529 Ом.
Необходимая информация Полученные значения
Объем выборки: n 25
Верхнее предельное значение: U 570
Нижнее предельное значение: L 470
Известное s 21,0
Нормированное s:![]() 0,21
0,21
Нормированные граничные значения для кривой приемки (рисунок 4) следующие
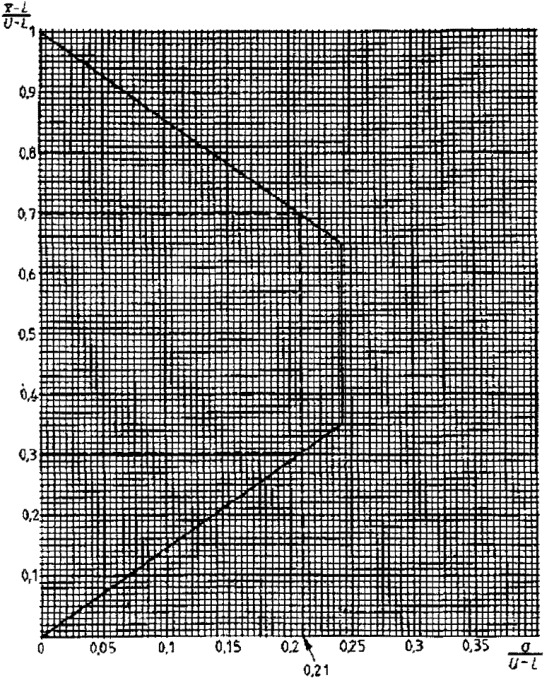
Рисунок 4 - Пример применения приемочной карты для предельных значений двустороннего допуска с общим AQL (s-метод)
Максимальное Минимальное
![]()
![]()
![]() =L+0,700(U-L)=470+70,0
=L+0,700(U-L)=470+70,0 ![]() =L+0,300(U-L)=470+30,0
=L+0,300(U-L)=470+30,0
Приемочные
значения для ![]() :
:
![]() =540,0
=540,0 ![]() =500,0
=500,0
Сумма измерений 12755
Среднее измерений 510,2
Так как ![]() =510,2 лежит между значениями 540,0 и 500,0, то партия должна
быть принята.
=510,2 лежит между значениями 540,0 и 500,0, то партия должна
быть принята.
Примечания
1 Все расчеты, за исключением двух последних строк, должны быть проведены до начала контроля.
2 Так как в этом примере
точки пересечения лежат на прямолинейных участках кривой приемки, приемочные
значения для ![]() могли быть просто
вычислены.
могли быть просто
вычислены.
Из таблицы IVs имеем:
fs =0,244,
MPSD=0,244(570-470)=24,4. Поскольку s<MPSD, то
требуется вычислить ![]() и
и ![]()
Из таблицы IIIA имеем:
k=1,42,
ks=29,8,
![]() = U-ks=540,2,
= U-ks=540,2,
![]() =L+ks=499,8
=L+ks=499,8
и снова партия со средним измерений 510,2 должна быть принята.
Примечание - Если известно, что s=25, то есть s>MPSD, то выборочный контроль не нужен.
16 Процедура непрерывного контроля
Планы выборочного контроля по количественному признаку могут эффективно работать только в том случае, если выполнены следующие условия:
a) контролируемый показатель качества имеет нормальное распределение;
b) производится запись результатов контроля;
c) выполняются правила переключения.
Необходимо убедиться в выполнении этих требований.
17 Условия нормальности и выбросы
17.1 Условия нормальности
Условия нормальности проверяются уполномоченной стороной перед началом выборочного контроля. В случае сомнения специалист по статистике принимает решение, подходит ли распределение для проведения выборочного контроля по количественному признаку или следует провести тесты на нормальность, как в ГОСТ Р 50779.72.
17.2 Выбросы
Выброс - это значение измеряемого показателя качества, значительно отличающееся от других измеренных значений в выборке. Одиночный выброс, даже лежащий в - пределах поля допуска, может привести к увеличению изменчивости процесса, изменению среднего выборки и, следовательно, к отклонению партии.
Если есть подозрение на наличие выбросов, перед принятием решения должен быть проведен тест на выбросы (например, по ИСО 5725.2). Когда выбросы обнаружены, действия в отношении-партии должны быть согласованы между поставщиком и потребителем.
18 Регистрация данных
18.1 Контрольные карты
Одно из преимуществ контроля по количественному признаку состоит в том, что изменения в уровне качества продукции могут быть обнаружены и предупреждены прежде, чем будет принято решение об отклонении партии. Но это возможно только в случае правильной регистрации данных в процессе наблюдения.
Для любого s-, s- или R-метода должны регистрироваться
значения характеристик ![]() и s или R
предпочтительно в форме контрольных карт. Это особенно важно для s-метода, чтобы иметь возможность проверить, находится
ли значение s, полученное из выборки, в
пределах заданного s.
и s или R
предпочтительно в форме контрольных карт. Это особенно важно для s-метода, чтобы иметь возможность проверить, находится
ли значение s, полученное из выборки, в
пределах заданного s.
Когда заданы предельные значения с общим уровнем качества, значение MSSD, заданное в таблице IVs (или MAR, заданное в таблице RIV), надо нанести на s-карту (или R-карту) как критерий неприемлемых значений.
Примечание - Контрольные карты используют для обнаружения отклонения. Решение о приемке каждой конкретной партии определяется процедурами, заданными в разделах 14 и 15.
18.2 Отклонение партии
Особое внимание надо уделять регистрации всех непринятых партий, а также тому, выполняются ли правила переключения.
Партия, отклоненная по установленному плану выборочного контроля, не должна повторно предъявляться на контроль (частично или полностью) без разрешения уполномоченной стороны.
19 Правила переключения
Стандартные правила переключения следующие:
19.1 В начале работы применяют нормальный контроль (если не предписан другой вид контроля), он продолжается до тех пор, пока не возникает необходимость усилить или ослабить контроль.
19.2 Усиленный контроль вводится тогда, когда хотя бы две партии из пяти последовательных партий (идущих друг за другом) отклонены.
Ужесточение контроля достигается за счет увеличения значения контрольного норматива. Значения заданы в таблице IIВ для s-метода и в таблице IIIB для s-метода (таблица RIIB для R-метода). В s-методе (и в R-методе) объем выборки не меняется до тех пор, пока не станет столь малым, что идущая вниз стрелка в таблице покажет, что объем выборки должен быть увеличен.
19.3 Усиленный контроль ослабляется, когда приняты пять последовательных партий. В этом случае возобновляется нормальный контроль.
19.4 Ослабленный контроль устанавливается после того, как 10 последовательных партий приняты при нормальном контроле при выполнении следующих условий:
a) эти партии также были бы приняты, если бы AQL стал на один шаг жестче;
Примечание - Если значения величины k для этого более жесткого AQL не заданы в таблице IIA, кривая приемки может быть достаточно точно экстраполирована на глаз по другим кривым соответствующей диаграммы из множества диаграмм для s-метода.
b) производственный процесс находится в статистически управляемом состоянии;
c) уполномоченная сторона признает требование ввести ослабленный контроль. Ослабленный контроль прекращается, и возобновляется нормальный контроль, если наступает одно из следующих событий:
a) партия не принимается;
b) производство становится нестабильным;
c) другие обстоятельства заставляют ввести нормальный контроль.
20 Прекращение и возобновление контроля
Если общее число отклоняемых партий в последовательности партий при усиленном контроле достигнет пяти, процедура приемки партий по данному стандарту должна быть прекращена.
В соответствии с настоящим стандартом контроль не возобновляется до тех пор, пока поставщиком не будут приняты меры по улучшению качества продукции (или услуги), после чего устанавливают усиленный контроль в соответствии с 19.2.
21 Кривые приемки для усиленного и ослабленного контроля
a) Кривые приемки отдельно для усиленного и нормального контроля отсутствуют, поэтому, если проводится усиленный или ослабленный контроль с заданными предельными значениями с общим уровнем качества, надо выбрать кривую приемки из множества кривых, соответствующих нормальному контролю (выбирается та кривая, которая соответствует требуемым объему выборки и приемочному числу).
b) При переключении на усиленный контроль требуемая кривая приемки может быть найдена с помощью таблицы IIА. Необходимая кривая может быть найдена среди кривых, используемых при нормальном контроле. Это кривая, соответствующая такому же объему выборки, но AQL на ступень ниже.
В некоторых случаях такое усиление контроля сопровождается увеличением объема выборки.
Если используется s-метод и s превышает MPSD (соответствующее AQL на ступень ниже), необходимо вернуться к усиленному контролю по s-методу.
c) При переключении на ослабленный контроль требуемая кривая приемки находится по таблице VIB. Эта кривая соответствует кривой для нормального контроля при AQL на ступень выше и объеме выборки - на три ступени ниже.
Пример - Применяется s-метод с кодом объема выборки I и AQL=0,25. Из таблицы VIA следует, что кривая приемки для усиленного контроля та же самая, что и кривая для нормального контроля с кодом объема выборки I и AQL=0,15.
Из таблице VIB следует, что кривая приемки для ослабленного контроля та же, что и кривая для нормального контроля с кодом объема выборки F и AQL=0,40.
22 Переключение на s-метод
Если оказывается, что значения s (или R)
контролируемы, а корень квадратный из среднего значения квадрата величины s (среднее взвешенное) (или ![]() R/c) может быть принят за s как известное стандартное отклонение процесса, то
применим s-метод.
R/c) может быть принят за s как известное стандартное отклонение процесса, то
применим s-метод.
Для того чтобы подтвердить, остается ли изменчивость процесса в состоянии статистической управляемости, следует по-прежнему вычислять и наносить на контрольную карту значения s (по А.2 приложения А).
Примечание - Не следует переходить на s-метод без разрешения уполномоченной стороны.
Глава IV ТАБЛИЦЫ И ДИАГРАММЫ
В настоящем стандарте применены следующие таблицы и диаграммы:
Таблицы
IA Коды объема выборки и уровни контроля
IB Коды объема выборки и объемы выборки для нормального контроля
IIА Одноступенчатые выборочные планы для нормального контроля (основная таблица): s-метод
IIВ Одноступенчатые выборочные планы для усиленного контроля (основная таблица): s-метод
IIС Одноступенчатые выборочные планы для ослабленного контроля (основная таблица): s-метод
IIIA Одноступенчатые выборочные планы для нормального контроля (основная таблица): s-метод
IIIB Одноступенчатые выборочные планы для усиленного контроля (основная таблица): s-метод
IIIC Одноступенчатые выборочные планы для ослабленного контроля (основная таблица): s-метод
IVs Значения коэффициента fs для максимального выборочного стандартного отклонения (MSSD): s-метод
IVs Значения коэффициента, для максимального выборочного стандартного отклонения процесса (MPSD): s-метод
VB-VP Таблицы и оперативные характеристики для одноступенчатых планов выборочного контроля (коды объемов выборки В-Р)
VIA Соответствие между планами усиленного и нормального контроля
VIB Соответствие между планами ослабленного и нормального контроля
Диаграммы
А Коды объема выборок стандартных планов выборочного контроля с установленным уровнем качества и вероятностью приемки 95 % и 10 %
s-D - s-P Кривые приемки для предельных значений с общим уровнем качества: s-метод
s-С - s-Р Кривые приемки для предельных значений с общим уровнем качества: s-метод
Таблица IА - Коды объема выборки и уровни контроля для специальных уровней контроля S-3, S-4 и общих уровней контроля I-III
|
Объем партии |
Специальные уровни контроля |
Общие уровни контроля |
|||
|
S-3 |
S-4 |
I |
II |
III |
|
|
От 2 до 8 включ. |
|
|
|
|
C |
|
» 9 » 15 » |
В |
D |
|||
|
» 16 » 25 » |
В |
С |
Е |
||
|
» 26 » 50 » |
С |
D |
F |
||
|
» 51 » 90 » |
В |
D |
Е |
G |
|
|
» 91 » 150 » |
С |
Е |
F |
Н |
|
|
» 151 » 280 » |
В |
D |
F |
G |
I |
|
» 281 » 500 » |
C |
Е |
G |
H/I*) |
J |
|
» 501 » 1200 » |
D |
F |
Н |
J |
К |
|
» 1201 » 3200 » |
Е |
G |
I |
К |
L |
|
» 3201 » 10000 » |
F |
Н |
J |
L |
М |
|
» 10001 » 35000 » |
G |
I |
К |
М |
N |
|
» 35001 » 150000 » |
Н |
J |
L |
N |
Р |
|
» 150001 » 500000 » |
I |
К |
М |
P |
|
|
Св. 500001 |
J |
L |
N |
|
|
|
*) Для объемов партии от 281 до 400 необходимо использовать код Н, для объемов партии от 401 до 500 - код I. Примечания 1 Коды объема выборки и уровни контроля в настоящем стандарте соответствуют приведенным в ГОСТ Р 50779.71. 2 Символ |
|||||
Таблица IB - Коды объема выборки и объемы выборки для нормального контроля: s- и s-методы
|
Код |
s- метод |
s-метод |
|
Эквивалентные значения по ГОСТ Р 50779.71 |
|||||||||||
|
AQL |
|
||||||||||||||
|
Объем выборки |
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,0 |
1,5 |
2,5 |
4,0 |
6,5 |
10,0 |
|
Код |
Объем выборки |
|
|
В |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
В |
3 |
|
C |
4 |
2 |
2 |
2 |
2 |
3 |
3 |
|
С |
5 |
|||||
|
D |
5 |
2 |
2 |
2 |
3 |
3 |
3 |
4 |
|
D |
8 |
||||
|
Е |
7 |
2 |
2 |
3 |
3 |
3 |
4 |
4 |
5 |
5 |
|
Е |
13 |
||
|
F |
10 |
3 |
3 |
3 |
4 |
4 |
4 |
5 |
5 |
6 |
7 |
|
F |
20 |
|
|
G |
15 |
4 |
4 |
4 |
5 |
5 |
6 |
6 |
7 |
8 |
9 |
11 |
|
G |
32 |
|
Н |
20 |
5 |
5 |
6 |
6 |
7 |
7 |
8 |
9 |
10 |
12 |
14 |
|
Н |
50 |
|
I |
25 |
6 |
6 |
7 |
8 |
8 |
9 |
10 |
11 |
13 |
15 |
17 |
|
- |
- |
|
J |
35 |
8 |
9 |
9 |
10 |
11 |
12 |
14 |
15 |
18 |
20 |
24 |
|
J |
80 |
|
К |
50 |
11 |
12 |
13 |
14 |
16 |
17 |
19 |
22 |
25 |
29 |
33 |
|
К |
125 |
|
L |
75 |
16 |
17 |
19 |
21 |
23 |
25 |
28 |
32 |
36 |
42 |
49 |
|
L |
200 |
|
М |
100 |
22 |
23 |
25 |
27 |
30 |
33 |
36 |
42 |
48 |
55 |
64 |
|
М |
315 |
|
N |
150 |
31 |
34 |
37 |
40 |
44 |
49 |
54 |
61 |
70 |
82 |
95 |
|
N |
500 |
|
Р |
200 |
42 |
45 |
49 |
54 |
59 |
65 |
71 |
81 |
93 |
109 |
127 |
|
Р |
800 |
|
Примечания 1 Все значения AQL выражены в процентах несоответствующих единиц продукции. 2 Коды объема выборки в настоящем стандарте соответствуют приведенным в ГОСТ Р 50779.71. 3 Символ |
|||||||||||||||
Таблица IIА - Одноступенчатые выборочные планы для нормального контроля (основная таблица): s-метод
|
Код объема выборки |
Объем выборки |
Приемлемые уровни качества AQL |
|||||||||||||
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,00 |
1,50 |
2,50 |
4,00 |
6,50 |
10,00 |
|||||
|
k |
k |
k |
k |
k |
k |
k |
k |
k |
k |
k |
|||||
|
В |
3 |
|
|
|
|
|
|
|
1,12 |
0,958 |
0,765 |
0,566 |
|||
|
С |
4 |
1,45 |
1,34 |
1,17 |
1,01 |
0,814 |
0,617 |
||||||||
|
D |
5 |
1,65 |
1,53 |
1,40 |
1,24 |
1,07 |
0,874 |
0,675 |
|||||||
|
Е |
7 |
2,00 |
1,88 |
1,75 |
1,62 |
1,50 |
1,33 |
1,15 |
0,955 |
0,755 |
|||||
|
F |
10 |
2,24 |
2,11 |
1,98 |
1,84 |
1,72 |
1,58 |
1,41 |
1,23 |
1,03 |
0,828 |
||||
|
G |
15 |
2,42 |
2,32 |
2,20 |
2,06 |
1,91 |
1,79 |
1,65 |
1,47 |
1,30 |
1,09 |
0,886 |
|||
|
Н |
20 |
2,47 |
2,36 |
2,24 |
2,11 |
1,96 |
1,82 |
1,69 |
1,51 |
1,33 |
1,12 |
0,917 |
|||
|
I |
25 |
2,50 |
2,40 |
2,26 |
2,14 |
1,98 |
1,85 |
1,72 |
1,53 |
1,35 |
1,14 |
0,936 |
|||
|
J |
35 |
2,54 |
2,45 |
2,31 |
2,18 |
2,03 |
1,89 |
1,76 |
1,57 |
1,39 |
1,18 |
0,969 |
|||
|
К |
50 |
2,60 |
2,50 |
2,35 |
2,22 |
2,08 |
1,93 |
1,80 |
1,61 |
1,42 |
1,21 |
1,00 |
|||
|
L |
75 |
2,66 |
2,55 |
2,41 |
2,27 |
2,12 |
1,98 |
1,84 |
1,65 |
1,46 |
1,24 |
|
1,03 |
||
|
М |
100 |
2,69 |
2,58 |
2,43 |
2,29 |
2,14 |
2,00 |
1,86 |
1,67 |
1,48 |
|
1,26 |
1,05 |
||
|
N |
150 |
2,73 |
2,61 |
2,47 |
2,33 |
2,18 |
2,03 |
1,89 |
1,70 |
|
1,51 |
1,29 |
1,07 |
||
|
Р |
200 |
2,73 |
2,62 |
2,47 |
2,33 |
2,18 |
2,04 |
1,89 |
|
1,51 |
1,29 |
1,07 |
|||
|
Примечания к таблицам IIA - IIIC: 1 Все значения AQL выражены в процентах несоответствующих единиц продукции. 2 Коды объема выборки в настоящем стандарте соответствуют приведенным в ГОСТ Р 50779.71. 3 Символы указывают:
|
|||||||||||||||
Таблица IIВ - Одноступенчатые выборочные планы для усиленного контроля (основная таблица): s-метод
|
Код объема выборки |
Объем выборки |
Приемлемые уровни качества |
||||||||||||||
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,00 |
1,50 |
2,50 |
4,00 |
6,50 |
10,00 |
||||||
|
k |
k |
k |
k |
k |
k |
k |
k |
k |
k |
k |
||||||
|
В |
3 |
|
|
|
|
|
|
|
|
1,12 |
0,958 |
0,765 |
||||
|
С |
4 |
1,45 |
1,34 |
1,17 |
1,01 |
0,814 |
||||||||||
|
D |
5 |
1,65 |
1,53 |
1,40 |
1,24 |
1,07 |
0,874 |
|||||||||
|
Е |
7 |
2,00 |
1,88 |
1,75 |
1,62 |
1,50 |
1,33 |
1,15 |
0,955 |
|||||||
|
F |
10 |
2,24 |
2,11 |
1,98 |
1,84 |
1,72 |
1,58 |
1,41 |
1,23 |
1,03 |
||||||
|
G |
15 |
2,53 |
2,42 |
2,32 |
2,20 |
2,06 |
1,91 |
1,79 |
1,65 |
1,47 |
1,30 |
1,09 |
||||
|
Н |
20 |
2,58 |
2,47 |
2,36 |
2,24 |
2,11 |
1,96 |
1,82 |
1,69 |
1,51 |
1,33 |
1,12 |
||||
|
I |
25 |
2,61 |
2,50 |
2,40 |
2,26 |
2,14 |
1,98 |
1,85 |
1,72 |
1,53 |
1,35 |
1,14 |
||||
|
J |
35 |
2,65 |
2,54 |
2,45 |
2,31 |
2,18 |
2,03 |
1,89 |
1,76 |
1,57 |
1,39 |
1,18 |
||||
|
К |
50 |
2,71 |
2,60 |
2,50 |
2,35 |
2,22 |
2,08 |
1,93 |
1,80 |
1,61 |
1,42 |
1,21 |
||||
|
L |
75 |
2,77 |
2,66 |
2,55 |
2,41 |
2,27 |
2,12 |
1,98 |
1,84 |
1,65 |
1,46 |
|
1,24 |
|||
|
М |
100 |
2,80 |
2,69 |
2,58 |
2,43 |
2,29 |
2,14 |
2,00 |
1,86 |
1,67 |
|
1,48 |
1,26 |
|||
|
N |
150 |
2,84 |
2,73 |
2,61 |
2,47 |
2,33 |
2,18 |
2,03 |
1,89 |
|
1,70 |
1,51 |
1,29 |
|||
|
Р |
200 |
2,85 |
2,73 |
2,62 |
2,47 |
2,33 |
2,18 |
2,04 |
|
1,89 |
1,70 |
1,51 |
1,29 |
|||
Таблица IIC - Одноступенчатые выборочные планы для ослабленного контроля (основная таблица): s-метод
|
Код объема выборки |
Объем выборки |
Приемлемые уровни качества (ослабленный контроль) |
||||||||||||||||
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,00 |
1,50 |
2,50 |
4,00 |
6,50 |
10,00 |
||||||||
|
k |
k |
k |
k |
k |
k |
k |
k |
k |
k |
k |
||||||||
|
В |
3 |
|
|
|
|
|
|
|
|
1,12 |
0,958 |
0,765 |
0,566 |
0,341 |
||||
|
C |
3 |
1,12 |
0,958 |
0,765 |
0,566 |
0,341 |
||||||||||||
|
D |
3 |
1,12 |
0,958 |
0,765 |
0,566 |
0,341 |
||||||||||||
|
Е |
3 |
|
|
1,12 |
0,958 |
0,765 |
0,566 |
0,341 |
||||||||||
|
F |
4 |
1,45 |
1,34 |
1,17 |
1,01 |
0,814 |
0,617 |
0,393 |
||||||||||
|
G |
5 |
1,65 |
1,53 |
1,40 |
1,24 |
1,07 |
0,874 |
0,675 |
0,455 |
|||||||||
|
Н |
7 |
2,00 |
1,88 |
1,75 |
1,62 |
1,50 |
1,33 |
1,15 |
0,955 |
0,755 |
0,536 |
|||||||
|
I |
10 |
2,24 |
2,11 |
1,98 |
1,84 |
1,72 |
1,58 |
1,41 |
1,23 |
1,03 |
0,828 |
0,611 |
||||||
|
J |
15 |
2,32 |
2,20 |
2,06 |
1,91 |
1,79 |
1,65 |
1,47 |
1,30 |
1,09 |
0,886 |
0,664 |
||||||
|
К |
20 |
2,36 |
2,24 |
2,11 |
1,96 |
1,82 |
1,69 |
1,51 |
1,33 |
1,12 |
0,917 |
0,695 |
||||||
|
L |
25 |
2,40 |
2,26 |
2,14 |
1,98 |
1,85 |
1,72 |
1,53 |
1,35 |
1,14 |
0,936 |
|
0,712 |
|||||
|
М |
35 |
2,45 |
2,31 |
2,18 |
2,03 |
1,89 |
1,76 |
1,57 |
1,39 |
1,18 |
|
0,969 |
0,745 |
|||||
|
N |
50 |
2,50 |
2,35 |
2,22 |
2,08 |
1,93 |
1,80 |
1,61 |
1,42 |
|
1,21 |
1,00 |
0,774 |
|||||
|
Р |
75 |
2,55 |
2,41 |
2,27 |
2,12 |
1,98 |
1,84 |
1,65 |
|
1,46 |
1,24 |
1,03 |
0,804 |
|||||
Таблица IIIA - Одноступенчатые выборочные планы для нормального контроля (основная таблица): s-метод
|
Код объема выборки |
Приемлемые уровни качества (нормальный контроль) |
||||||||||||||||||||||||||||||||||||||||||||
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,00 |
1,50 |
2,50 |
4,00 |
6,50 |
10,00 |
|||||||||||||||||||||||||||||||||||
|
п |
k |
п |
k |
n |
k |
п |
k |
n |
k |
п |
k |
п |
k |
п |
k |
п |
k |
п |
k |
n |
k |
||||||||||||||||||||||||
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
C |
|
|
|
|
|
|
|
|
|
|
2 |
|
1,36 |
2 |
|
1,25 |
2 |
|
1,09 |
2 |
|
0,936 |
3 |
|
0,755 |
3 |
|
0,573 |
|||||||||||||||||
|
D |
|
|
|
|
|
|
|
|
2 |
|
1,58 |
2 |
|
1,42 |
2 |
|
1,33 |
3 |
|
1,17 |
3 |
|
1,01 |
3 |
|
0,825 |
4 |
|
0,641 |
||||||||||||||||
|
E |
|
|
|
|
2 |
|
1,94 |
2 |
|
1,81 |
3 |
|
1,69 |
3 |
|
1,69 |
3 |
|
1,44 |
4 |
|
1,28 |
4 |
|
1,11 |
5 |
|
0,919 |
5 |
|
0,728 |
||||||||||||||
|
F |
|
|
3 |
|
2,19 |
3 |
|
2,07 |
3 |
|
1,91 |
4 |
|
1,80 |
4 |
|
1,69 |
4 |
|
1,53 |
5 |
|
1,39 |
5 |
|
1,20 |
6 |
|
0,991 |
7 |
|
0,797 |
|||||||||||||
|
G |
4 |
|
2,39 |
4 |
|
2,30 |
4 |
|
2,14 |
5 |
|
2,05 |
5 |
|
1,88 |
6 |
|
1,78 |
6 |
|
1,62 |
7 |
|
1,45 |
8 |
|
1,28 |
9 |
|
1,07 |
11 |
|
0,877 |
||||||||||||
|
H |
5 |
|
2,46 |
5 |
|
2,34 |
6 |
|
2,33 |
6 |
|
2,08 |
7 |
|
1,95 |
7 |
|
1,80 |
8 |
|
1,68 |
9 |
|
1,49 |
10 |
|
1,31 |
12 |
|
1,11 |
14 |
|
0,906 |
||||||||||||
|
I |
6 |
|
2,49 |
6 |
|
2,37 |
7 |
|
2,25 |
8 |
|
2,13 |
8 |
|
1,96 |
9 |
|
1,83 |
10 |
|
1,70 |
11 |
|
1,51 |
13 |
|
1,34 |
15 |
|
1,13 |
17 |
|
0,924 |
||||||||||||
|
J |
8 |
|
2,54 |
9 |
|
2,45 |
9 |
|
2,29 |
10 |
|
2,16 |
11 |
|
2,01 |
12 |
|
1,88 |
14 |
|
1,75 |
15 |
|
1,56 |
18 |
|
1,38 |
20 |
|
1,17 |
24 |
|
0,964 |
||||||||||||
|
K |
11 |
|
2,59 |
12 |
|
2,49 |
13 |
|
2,35 |
14 |
|
2,21 |
16 |
|
2,07 |
17 |
|
1,83 |
19 |
|
1,79 |
22 |
|
1,61 |
25 |
|
1,42 |
29 |
|
1,21 |
33 |
|
0,995 |
||||||||||||
|
L |
16 |
|
2,65 |
17 |
|
2,54 |
19 |
|
2,41 |
21 |
|
2,27 |
23 |
|
2,12 |
25 |
|
1,97 |
28 |
|
1,84 |
32 |
|
1,65 |
36 |
|
1,46 |
42 |
|
1,24 |
49 |
|
1,03 |
||||||||||||
|
M |
22 |
|
2,69 |
23 |
|
2,57 |
25 |
|
2,43 |
27 |
|
2,29 |
30 |
|
2,14 |
33 |
|
2,00 |
36 |
|
1,86 |
42 |
|
1,67 |
48 |
|
1,48 |
55 |
|
1,26 |
64 |
1,05 |
|||||||||||||
|
N |
31 |
|
2,72 |
34 |
|
2,62 |
37 |
|
2,47 |
40 |
|
2,33 |
44 |
|
2,17 |
49 |
|
2,03 |
54 |
|
1,89 |
61 |
|
1,69 |
70 |
|
1,51 |
82 |
1,29 |
95 |
1,07 |
||||||||||||||
|
P |
42 |
|
2,73 |
45 |
|
2,62 |
49 |
|
2,48 |
54 |
|
2,34 |
59 |
|
2,18 |
65 |
|
2,04 |
71 |
|
1,89 |
81 |
|
1,70 |
93 |
1,51 |
109 |
1,29 |
127 |
1,07 |
|||||||||||||||
Таблица IIIB - Одноступенчатые выборочные планы для усиленного контроля основная таблица): s-метод
|
Код объема выборки |
Приемлемые уровни качества (усиленный контроль) |
|||||||||||||||||||||||||||||||||||||||||||
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,00 |
1,50 |
2,50 |
4,00 |
6,50 |
10,00 |
||||||||||||||||||||||||||||||||||
|
п |
k |
п |
k |
п |
k |
п |
k |
п |
k |
п |
k |
п |
k |
п |
k |
n |
k |
п |
k |
n |
k |
|||||||||||||||||||||||
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1,36 |
2 |
|
1,25 |
2 |
|
1,09 |
2 |
|
0,936 |
3 |
|
0,755 |
|||||||||||||||||
|
D |
|
|
|
|
|
|
|
|
|
|
2 |
|
1,58 |
2 |
|
1,42 |
2 |
|
1,33 |
3 |
|
1,17 |
3 |
|
1,01 |
3 |
|
0,825 |
||||||||||||||||
|
E |
|
|
|
|
|
|
2 |
|
1,94 |
2 |
|
1,81 |
3 |
|
1,69 |
3 |
|
1,56 |
3 |
|
1,44 |
4 |
|
1,23 |
4 |
|
1,11 |
5 |
|
0,919 |
||||||||||||||
|
F |
|
|
|
|
3 |
|
2,19 |
3 |
|
2,07 |
3 |
|
1,91 |
4 |
|
1,80 |
4 |
|
1,69 |
4 |
|
1,53 |
5 |
|
1,39 |
5 |
|
1,20 |
6 |
|
0,991 |
|||||||||||||
|
G |
3 |
|
2,49 |
4 |
|
2,39 |
4 |
|
2,30 |
4 |
|
2,14 |
5 |
|
2,05 |
5 |
|
1,88 |
6 |
|
1,78 |
6 |
|
1,62 |
7 |
|
1,45 |
8 |
|
1,28 |
9 |
|
1,07 |
|||||||||||
|
H |
4 |
|
2,55 |
5 |
|
2,46 |
5 |
|
2,34 |
6 |
|
2,23 |
6 |
|
2,08 |
7 |
|
1,95 |
7 |
|
1,80 |
8 |
|
1,68 |
9 |
|
1,49 |
10 |
|
1,31 |
12 |
|
1,11 |
|||||||||||
|
I |
6 |
|
2,59 |
6 |
|
2,49 |
6 |
|
2,37 |
7 |
|
2,25 |
8 |
|
2,13 |
8 |
|
1,96 |
9 |
|
1,83 |
10 |
|
1,70 |
11 |
|
1,51 |
13 |
|
1,34 |
15 |
|
1,13 |
|||||||||||
|
J |
7 |
|
2,63 |
8 |
|
2,54 |
9 |
|
2,45 |
9 |
|
2,29 |
10 |
|
2,16 |
11 |
|
2,01 |
12 |
|
1,86 |
14 |
|
1,75 |
15 |
|
1,56 |
18 |
|
1,38 |
20 |
|
1,17 |
|||||||||||
|
K |
11 |
|
2,72 |
11 |
|
2,59 |
12 |
|
2,49 |
13 |
|
2,35 |
14 |
|
2,21 |
16 |
|
2,07 |
17 |
|
1,93 |
19 |
|
1,79 |
22 |
|
1,61 |
25 |
|
1,42 |
29 |
|
1,21 |
|||||||||||
|
L |
15 |
|
2,77 |
16 |
|
2,65 |
17 |
|
2,54 |
19 |
|
2,41 |
21 |
|
2,27 |
23 |
|
2,12 |
25 |
|
1,97 |
28 |
|
1,84 |
32 |
|
1,65 |
36 |
|
1,46 |
42 |
|
1,24 |
|||||||||||
|
M |
20 |
|
2,80 |
22 |
|
2,69 |
23 |
|
2,57 |
25 |
|
2,43 |
27 |
|
2,29 |
30 |
|
2,14 |
33 |
|
2,00 |
36 |
|
1,86 |
42 |
|
1,67 |
48 |
|
1,48 |
55 |
1,26 |
||||||||||||
|
N |
30 |
|
2,84 |
31 |
|
2,72 |
34 |
|
2,62 |
37 |
|
2,47 |
40 |
|
2,33 |
44 |
|
2,17 |
49 |
|
2,03 |
54 |
|
1,89 |
61 |
|
1,69 |
70 |
1,51 |
82 |
1,29 |
|||||||||||||
|
P |
40 |
|
2,85 |
42 |
|
2,73 |
45 |
|
2,62 |
49 |
|
2,48 |
54 |
|
2,34 |
59 |
|
2,18 |
65 |
|
2,04 |
71 |
|
1,89 |
81 |
1,70 |
93 |
1,51 |
109 |
1,29 |
||||||||||||||
Таблица IIIC - Одноступенчатые выборочные планы для ослабленного контроля (основная таблица): s-метод
|
Код объема выборки |
Приемлемые уровни качества (ослабленный контроль) |
||||||||||||||||||||||||||||||||||||||||||
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,00 |
1,50 |
2,50 |
4,00 |
6,50 |
10,00 |
|||||||||||||||||||||||||||||||||
|
п |
k |
n |
k |
п |
k |
n |
k |
n |
k |
n |
k |
n |
k |
n |
k |
п |
k |
n |
k |
n |
k |
||||||||||||||||||||||
|
В |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
F |
|
|
|
|
|
|
|
|
2 |
|
1,36 |
2 |
|
1,25 |
2 |
|
1,09 |
2 |
|
0,936 |
3 |
|
0,755 |
3 |
|
0,573 |
4 |
|
0,344 |
||||||||||||||
|
G |
|
|
|
|
|
|
2 |
|
1,58 |
2 |
|
1,42 |
2 |
|
1,30 |
3 |
|
1,17 |
3 |
|
1,01 |
3 |
|
0,825 |
4 |
|
0,641 |
4 |
|
0,429 |
|||||||||||||
|
Н |
|
|
2 |
|
1,94 |
2 |
|
1,81 |
3 |
|
1,69 |
3 |
|
1,56 |
3 |
|
1,44 |
4 |
|
1,28 |
4 |
|
1,11 |
5 |
|
0,919 |
5 |
|
0,728 |
6 |
|
0,515 |
|||||||||||
|
I |
3 |
|
2,19 |
3 |
|
2,07 |
3 |
|
1,91 |
4 |
|
1,80 |
4 |
|
1,69 |
4 |
|
1,53 |
5 |
|
1,39 |
5 |
|
1,20 |
6 |
|
0,991 |
7 |
|
0,797 |
8 |
|
0,584 |
||||||||||
|
J |
4 |
|
2,30 |
4 |
|
2,14 |
5 |
|
2,05 |
5 |
|
1,88 |
6 |
|
1,78 |
6 |
|
1,62 |
7 |
|
1,45 |
8 |
|
1,28 |
9 |
|
1,07 |
11 |
|
0,877 |
12 |
|
0,649 |
||||||||||
|
К |
5 |
|
2,34 |
6 |
|
2,23 |
6 |
|
2,08 |
7 |
|
1,95 |
7 |
|
1,80 |
8 |
|
1,68 |
9 |
|
1,49 |
10 |
|
1,31 |
12 |
|
1,11 |
14 |
|
0,906 |
16 |
|
0,685 |
||||||||||
|
L |
6 |
|
2,37 |
7 |
|
2,25 |
8 |
|
2,13 |
8 |
|
1,96 |
9 |
|
1,83 |
10 |
|
1,70 |
11 |
|
1,51 |
13 |
|
1,34 |
15 |
|
1,13 |
17 |
|
0,924 |
20 |
|
0,706 |
||||||||||
|
М |
9 |
|
2,45 |
9 |
|
2,29 |
10 |
|
2,16 |
11 |
|
2,01 |
12 |
|
1,88 |
14 |
|
1,75 |
15 |
|
1,56 |
18 |
|
1,38 |
20 |
|
1,17 |
24 |
|
0,964 |
27 |
0,737 |
|||||||||||
|
N |
12 |
|
2,49 |
13 |
|
2,35 |
14 |
|
2,21 |
16 |
|
2,07 |
17 |
|
1,93 |
19 |
|
1,79 |
22 |
|
1,61 |
25 |
|
1,42 |
29 |
|
1,21 |
33 |
0,995 |
38 |
0,770 |
||||||||||||
|
Р |
17 |
|
2,54 |
19 |
|
2,41 |
21 |
|
2,27 |
23 |
|
2,12 |
25 |
|
1,97 |
28 |
|
1,84 |
32 |
|
1,65 |
36 |
|
1,46 |
42 |
1,24 |
49 |
1,03 |
56 |
0,803 |
|||||||||||||
Таблица IVs - Значения коэффициента, для максимального выборочного стандартного отклонения (MSSD): s-метод
|
Объем выборки |
Приемлемые уровни качества (нормальный контроль) |
||||||||||||
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,00 |
1,50 |
2,50 |
4,00 |
6,50 |
10,00 |
|
|
|
3 |
|
|
|
|
|
|
|
|
0,436 |
0,453 |
0,475 |
0,502 |
0,538 |
|
4 |
|
|
|
|
|
|
0,339 |
0,353 |
0,374 |
0,399 |
0,432 |
0,472 |
0,528 |
|
5 |
|
|
|
|
|
0,294 |
0,308 |
0,323 |
0,346 |
0,372 |
0,408 |
0,452 |
0,511 |
|
7 |
|
|
|
0,242 |
0,253 |
0,266 |
0,280 |
0,295 |
0,318 |
0,345 |
0,381 |
0,425 |
0,485 |
|
10 |
|
|
0,214 |
0,224 |
0,235 |
0,248 |
0,261 |
0,276 |
0,298 |
0,324 |
0,359 |
0,403 |
0,460 |
|
15 |
0,188 |
0,195 |
0,202 |
0,211 |
0,222 |
0,235 |
0,248 |
0,262 |
0,284 |
0,309 |
0,344 |
0,386 |
0,442 |
|
20 |
0,183 |
0,190 |
0,197 |
0,206 |
0,216 |
0,229 |
0,242 |
0,255 |
0,277 |
0,302 |
0,336 |
0,377 |
0,432 |
|
25 |
0,180 |
0,187 |
0,193 |
0,203 |
0,212 |
0,225 |
0,238 |
0,251 |
0,273 |
0,297 |
0,331 |
0,372 |
0,426 |
|
35 |
0,176 |
0,183 |
0,189 |
0,198 |
0,208 |
0,220 |
0,232 |
0,245 |
0,266 |
0,291 |
0,323 |
0,364 |
0,416 |
|
50 |
0,172 |
0,178 |
0,184 |
0,194 |
0,203 |
0,214 |
0,227 |
0,241 |
0,261 |
0,284 |
0,317 |
0,356 |
0,408 |
|
75 |
0,168 |
0,174 |
0,181 |
0,189 |
0,199 |
0,211 |
0,223 |
0,235 |
0,255 |
0,279 |
0,310 |
0,348 |
0,399 |
|
100 |
0,166 |
0,172 |
0,179 |
0,187 |
0,197 |
0,208 |
0,220 |
0,233 |
0,253 |
0,276 |
0,307 |
0,345 |
0,395 |
|
150 |
0,163 |
0,170 |
0,175 |
0,185 |
0,193 |
0,206 |
0,216 |
0,230 |
0,249 |
0,271 |
0,302 |
0,341 |
0,388 |
|
200 |
0,163 |
0,168 |
0,175 |
0,183 |
0,193 |
0,203 |
0,215 |
0,228 |
0,248 |
0,269 |
0,302 |
0,338 |
0,386 |
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,00 |
1,50 |
2,50 |
4,00 |
6,50 |
10,00 |
|
|
|
Приемлемые уровни качества (усиленный контроль) |
|||||||||||||
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,00 |
1,50 |
2,50 |
4,00 |
6,50 |
10,00 |
||
|
Приемлемые уровни качества (ослабленный контроль) |
|||||||||||||
|
Примечание - MSSD получают путем умножения коэффициента fs на разность между верхним U и нижним L пределами поля допуска, то есть MSSD=fs(U-L). MSSD указывает наибольшее допустимое значение выборочного стандартного отклонения при использовании планов с двусторонним допуском в случае с неизвестной дисперсией. Если выборочное стандартное отклонение меньше MSSD, то нет гарантии, что партия будет принята. |
|||||||||||||
Таблица IVs - Значения коэффициента fs для максимального выборочного стандартного отклонения (MPSD): s-метод
|
Приемлемые уровни качества (нормальный контроль) |
|
||||||||||||
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,00 |
1,50 |
2,50 |
4,00 |
6,50 |
10,00 |
|
|
|
0,147 |
0,152 |
0,157 |
0,165 |
0,174 |
0,184 |
0,194 |
0,206 |
0,223 |
0,243 |
0,271 |
0,304 |
0,347 |
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,00 |
1,50 |
2,50 |
4,00 |
6,50 |
10,00 |
|
|
|
|
Приемлемые уровни качества (усиленный контроль) |
|
||||||||||||
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,00 |
1,50 |
2,50 |
4,00 |
6,50 |
10,00 |
|
|
|
Приемлемые уровни качества (ослабленный контроль) |
|
||||||||||||
|
Примечание- MPSD получают путем умножения коэффициента fs на разность между верхним U и нижним L пределами поля допуска, то есть MPSD=fs(U-L). MPSD указывает наибольшее допустимое значение выборочного стандартного отклонения при использовании планов с двусторонним допуском в случае с известной дисперсией. По решению уполномоченной стороны значения fs для усиленного контроля можно использовать при нормальном и ослабленном контроле, в этом случае выбор между s-методом и s-методом не зависит от правил переключения. |
|||||||||||||
Таблица VB - Код объема выборки В
График VB - Оперативные характеристики для одноступенчатых выборочных планов контроля
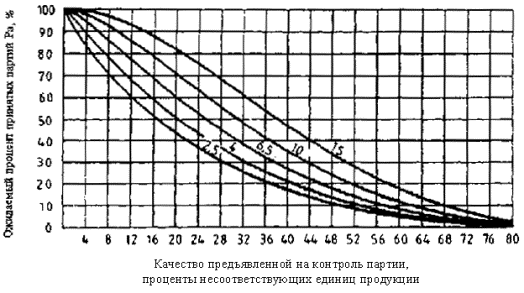
Таблица VB-1- Табличные значения оперативных характеристик для одноступенчатых выборочных планов контроля
|
Ра |
Приемлемые уровни качества (нормальный контроль) |
Ра |
|||||||||||
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,0 |
1,5 |
2,5 |
4,0 |
6,5 |
10,0 |
||
|
99,0 |
|
|
|
|
|
|
|
|
0,18 |
0,44 |
1,07 |
2,28 |
99,0 |
|
95,0 |
|
|
|
|
|
|
|
|
1,04 |
1,89 |
3,52 |
6,02 |
95,0 |
|
90,0 |
|
|
|
|
|
|
|
|
2,26 |
3,65 |
6,03 |
9,39 |
90,0 |
|
75,0 |
|
|
|
|
|
|
|
|
6,66 |
9,18 |
12,95 |
17,71 |
75,0 |
|
50,0 |
|
|
|
|
|
|
|
|
16,68 |
20,30 |
25,22 |
30,97 |
50,0 |
|
25,0 |
|
|
|
|
|
|
|
|
32,40 |
36,35 |
41,45 |
47,14 |
25,0 |
|
10,0 |
|
|
|
|
|
|
|
|
49,34 |
52,83 |
57,24 |
62,08 |
10,0 |
|
5,0 |
|
|
|
|
|
|
|
|
59,45 |
62,44 |
66,20 |
70,30 |
5,0 |
|
1,0 |
|
|
|
|
|
|
|
|
75,99 |
77,93 |
80,34 |
82,98 |
1,0 |
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,0 |
1,5 |
2,5 |
4,0 |
6,5 |
10,0 |
|
|
|
Приемлемые уровни качества (усиленный контроль) |
|||||||||||||
Таблица VC - Код объема выборки С
График VC - Оперативные характеристики для одноступенчатых выборочных планов контроля

Таблица VC-1 - Табличные значения оперативных характеристик для одноступенчатых выборочных планов контроля
|
Ра |
Приемлемые уровни качества (нормальный контроль) |
Ра |
|||||||||||
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,0 |
1,5 |
2,5 |
4,0 |
6,5 |
10,0 |
||
|
99,0 |
|
|
|
|
|
|
0,07 |
0,13 |
0,32 |
0,69 |
1,55 |
3,05 |
99,0 |
|
95,0 |
|
|
|
|
|
|
0,44 |
0,69 |
1,32 |
2,29 |
4,13 |
6,85 |
95,0 |
|
90,0 |
|
|
|
|
|
|
1,02 |
1,48 |
2,53 |
3,98 |
6,51 |
10,00 |
90,0 |
|
75,0 |
|
|
|
|
|
|
3,36 |
4,37 |
6,37 |
8,81 |
12,61 |
17,35 |
75,0 |
|
50,0 |
|
|
|
|
|
|
9,52 |
11,28 |
14,44 |
17,93 |
22,89 |
28,61 |
50,0 |
|
25,0 |
|
|
|
|
|
|
20,81 |
23,11 |
27,00 |
31,02 |
36,43 |
42,37 |
25,0 |
|
10,0 |
|
|
|
|
|
|
34,88 |
37,26 |
41,15 |
45,05 |
50,13 |
55,55 |
10,0 |
|
5,0 |
|
|
|
|
|
|
44,29 |
46,53 |
50,14 |
53,72 |
58,33 |
68,20 |
5,0 |
|
1,0 |
|
|
|
|
|
|
61,76 |
63,48 |
66,23 |
68,95 |
72,37 |
75,98 |
1,0 |
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,0 |
1,5 |
2,5 |
4,0 |
6,5 |
10,0 |
|
|
|
Приемлемые уровни качества (усиленный контроль) |
|||||||||||||
Таблица VD - Код объема выборки D
График VD - Оперативные характеристики для одноступенчатых выборочных планов контроля
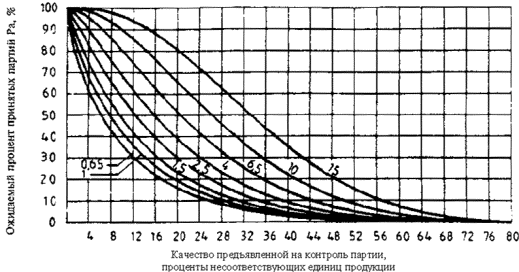
Таблица VD-1 - Табличные значения оперативных характеристик для одноступенчатых выборочных планов контроля
|
Ра |
Приемлемые уровни качества (нормальный контроль) |
Ра |
|||||||||||
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,0 |
1,5 |
2,5 |
4,0 |
6,5 |
10,0 |
||
|
99,0 |
|
|
|
|
|
0,04 |
0,09 |
0,18 |
0,40 |
0,84 |
1,79 |
3,44 |
99,0 |
|
95,0 |
|
|
|
|
|
0,28 |
0,46 |
0,77 |
1,38 |
2,43 |
4,30 |
7,11 |
95,0 |
|
90,0 |
|
|
|
|
|
0,64 |
0,98 |
1,51 |
2,48 |
3,99 |
6-,49 |
10,00 |
90,0 |
|
75,0 |
|
|
|
|
|
2,15 |
2,93 |
4,02 |
5,78 |
8,23 |
11,89 |
16,55 |
75,0 |
|
50,0 |
|
|
|
|
|
6,34 |
7,82 |
9,71 |
12,47 |
15,97 |
20,75 |
26,40 |
50,0 |
|
25,0 |
|
|
|
|
|
14,64 |
16,79 |
19,36 |
22,88 |
27,06 |
32,43 |
38,46 |
25,0 |
|
10,0 |
|
|
|
|
|
25,94 |
28,40 |
31,24 |
34,98 |
39,25 |
44,55 |
50,32 |
10,0 |
|
5,0 |
|
|
|
|
|
34,06 |
36,52 |
39,33 |
42,97 |
47,06 |
52,06 |
57,42 |
5,0 |
|
1,0 |
|
|
|
|
|
50,47 |
52,63 |
55,04 |
58,11 |
61,51 |
65,57 |
69,89 |
1,0 |
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,0 |
1,5 |
2,5 |
4,0 |
6,5 |
10,0 |
|
|
|
Приемлемые уровни качества (усиленный контроль) |
|||||||||||||
Таблица VE - Код объема выборки Е
График VE - Оперативные характеристики для одноступенчатых выборочных планов контроля

Таблица VE-1 - Табличные значения оперативных характеристик для одноступенчатых выборочных планов контроля
|
Ра |
Приемлемые уровни качества (нормальный контроль) |
Ра |
|||||||||||
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,0 |
1,5 |
2,5 |
4,0 |
6,5 |
10,0 |
||
|
99,0 |
|
|
|
0,02 |
0,03 |
0,07 |
0,14 |
0,25 |
0,53 |
1,09 |
2,19 |
4,04 |
99,0 |
|
95,0 |
|
|
|
0,11 |
0,18 |
0,32 |
0,53 |
0,83 |
1,50 |
2,65 |
4,57 |
7,46 |
95,0 |
|
90,0 |
|
|
|
0,25 |
0,40 |
0,64 |
1,01 |
1,48 |
2,47 |
4,04 |
6,50 |
9,99 |
90,0 |
|
75,0 |
|
|
|
0,90 |
1,27 |
1,83 |
2,58 |
3,47 |
5,15 |
7,56 |
11,00 |
15,49 |
75,0 |
|
50,0 |
|
|
|
2,89 |
3,72 |
4,83 |
6,18 |
7,69 |
10,28 |
13,66 |
18,11 |
23,53 |
50,0 |
|
25,0 |
|
|
|
7,38 |
8,80 |
10,57 |
12,60 |
14,71 |
18,11 |
22,27 |
27,41 |
33,35 |
25,0 |
|
10,0 |
|
|
|
14,42 |
16,33 |
18,60 |
21,09 |
23,58 |
27,43 |
31,93 |
37,28 |
43,25 |
10,0 |
|
5,0 |
|
|
|
20,09 |
22,20 |
24,65 |
27,29 |
29,88 |
33,82 |
38,33 |
43,60 |
49,38 |
5,0 |
|
1,0 |
|
|
|
33,10 |
35,32 |
37,83 |
40,45 |
42,95 |
46,72 |
50,89 |
55,64 |
60,73 |
1,0 |
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,0 |
1,5 |
2,5 |
4,0 |
6,5 |
10,0 |
|
|
|
Приемлемые уровни качества (усиленный контроль) |
|||||||||||||
Таблица VF - Код объема выборки F
График VF - Оперативные характеристики для одноступенчатых выборочных планов контроля


Таблица VF-1 - Табличные значения оперативных характеристик для одноступенчатых выборочных планов контроля
|
Ра |
Приемлемые уровни качества (нормальный контроль) |
Ра |
|||||||||||
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,0 |
1,5 |
2,5 |
4,0 |
6,5 |
10,0 |
||
|
99,0 |
|
|
0,01 |
0,03 |
0,05 |
0,11 |
0,19 |
0,35 |
0,69 |
1,35 |
2,62 |
4,69 |
99,0 |
|
95,0 |
|
|
0,07 |
0,12 |
0,21 |
0,36 |
0,57 |
0,94 |
1,65 |
2,83 |
4,84 |
7,81 |
95,0 |
|
90,0 |
|
|
0,15 |
0,25 |
0,40 |
0,66 |
0,98 |
1,52 |
2,50 |
4,04 |
6,52 |
10,01 |
90,0 |
|
75,0 |
|
|
0,49 |
0,74 |
1,08 |
1,61 |
2,21 |
3,15 |
4,70 |
6,93 |
10,25 |
14,60 |
75,0 |
|
50,0 |
|
|
1,53 |
2,08 |
2,79 |
3,77 |
4,82 |
6,33 |
8,62 |
11,69 |
15,91 |
21,09 |
50,0 |
|
25,0 |
|
|
3,93 |
4,95 |
6,16 |
7,72 |
9,29 |
11,41 |
14,45 |
18,25 |
23,20 |
28,96 |
25,0 |
|
10,0 |
|
|
7,95 |
9,44 |
11,15 |
13,23 |
15,23 |
17,84 |
21,40 |
25,66 |
30,99 |
36,98 |
10,0 |
|
5,0 |
|
|
11,40 |
13,17 |
15,13 |
17,47 |
19,68 |
22,49 |
26,27 |
30,68 |
36,09 |
42,06 |
5,0 |
|
1,0 |
|
|
20,10 |
22,24 |
24,53 |
27,19 |
29,58 |
32,59 |
36,50 |
40,92 |
46,18 |
51,82 |
1,0 |
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,0 |
1,5 |
2,5 |
4,0 |
6,5 |
10,0 |
|
|
|
Приемлемые уровни качества (усиленный контроль) |
|||||||||||||
Таблица VG - Код объема выборки G
График VG - Оперативные характеристики для одноступенчатых выборочных планов контроля
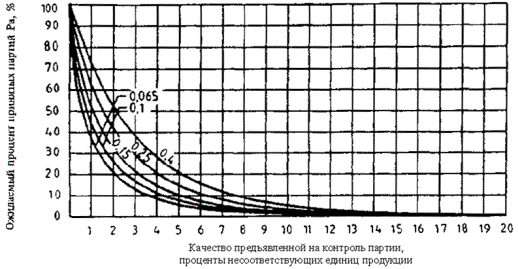

Таблица VG-1 - Табличные значения оперативных характеристик для одноступенчатых выборочных планов контроля
|
Ра |
Приемлемые уровни качества (нормальный контроль) |
Ра |
|||||||||||
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,0 |
1,5 |
2,5 |
4,0 |
6,5 |
10,0 |
||
|
99,0 |
0,01 |
0,01 |
0,02 |
0,04 |
0,08 |
0,17 |
0,28 |
0,49 |
0,96 |
1,71 |
3,23 |
5,58 |
99,0 |
|
95,0 |
0,03 |
0,06 |
0,09 |
0,15 |
0,25 |
0,45 |
0,68 |
1,09 |
1,91 |
3,09 |
5,30 |
8,41 |
95,0 |
|
90,0 |
0,07 |
0,11 |
0,17 - |
0,26 |
0,43 |
0,72 |
1,06 |
1,61 |
2,67 |
4,14 |
6,76 |
10,30 |
90,0 |
|
75,0 |
0,22 |
0,32 |
0,45 |
0,65 |
0,98 |
1,50 |
2,07 |
2,94 |
4,49 |
6,50 |
9,83 |
14,09 |
75,0 |
|
50,0 |
0,67 |
0,90 |
1,17 |
1,57 |
2,20 |
3,09 |
3,99 |
5,32 |
7,51 |
10,15 |
14,27 |
19,25 |
50,0 |
|
25,0 |
1,73 |
2,18 |
2,67 |
3,38 |
4,41 |
5,77 |
7,09 |
8,92 |
11,77 |
15,02 |
19,84 |
25,38 |
25,0 |
|
10,0 |
3,58 |
4,31 |
5,07 |
6,13 |
7,58 |
9,41 |
11,12 |
13,38 |
16,77 |
20,48 |
25,76 |
31,63 |
10,0 |
|
5,0 |
5,27 |
6,19 |
7,13 |
8,40 |
10,11 |
12,22 |
14,13 |
16,63 |
20,28 |
24,20 |
29,67 |
35,63 |
5,0 |
|
1,0 |
9,91 |
11,18 |
12,45 |
14,11 |
16,24 |
18,76 |
21,00 |
23,83 |
27,82 |
31,97 |
37,57 |
43,50 |
1,0 |
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,0 |
1,5 |
2,5 |
4,0 |
6,5 |
10,0 |
|
|
|
Приемлемые уровни качества (усиленный контроль) |
|||||||||||||
Таблица VH - Код объема выборки Н
График VH - Оперативные характеристики для одноступенчатых выборочных планов контроля

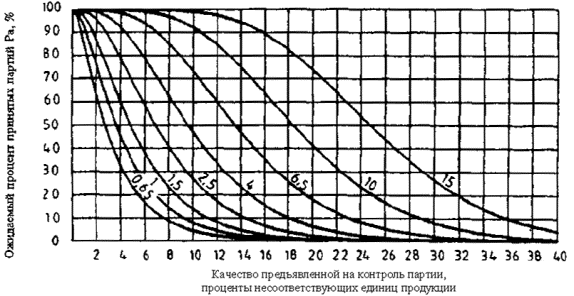
Таблица VH-1 - Табличные значения оперативных характеристик для одноступенчатых выборочных планов контроля
|
Ра |
Приемлемые уровни качества (нормальный контроль) |
Ра |
|||||||||||
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,0 |
1,5 |
2,5 |
4,0 |
6,5 |
10,0 |
||
|
99,0 |
|
0,02 |
0,04 |
0,06 |
0,11 |
0,21 |
0,37 |
0,61 |
1,15 |
2,04 |
3,73 |
6,25 |
99,0 |
|
95,0 |
0,04 |
0,07 |
0,11 |
0,17 |
0,29 |
0,49 |
0,79 |
1,21 |
2,07 |
3,39 |
5,69 |
8,88 |
95,0 |
|
90,0 |
0,08 |
0,12 |
0,19 |
0,29 |
0,45 |
0,75 |
1,15 |
1,69 |
2,77 |
4,35 |
7,01 |
10,58 |
90,0 |
|
75,0 |
0,21 |
0,31 |
0,44 |
0,63 |
0,93 |
1,42 |
2,06 |
2,85 |
4,35 |
6,43 |
9,71 |
13,89 |
75,0 |
|
50,0 |
0,56 |
0,76 |
1,01 |
1,38 |
1,90 |
2,69 |
3,66 |
4,81 |
6,85 |
9,51 |
13,49 |
18,31 |
50,0 |
|
25,0 |
1,31 |
1,68 |
2,13 |
2,74 |
3,56 |
4,75 |
6,12 |
7,67 |
10,29 |
13,52 |
18,13 |
23,47 |
25,0 |
|
10,0 |
2,58 |
3,16 |
3,85 |
4,73 |
5,88 |
7,46 |
9,23 |
11,14 |
14,25 |
17,94 |
23,01 |
28,70 |
10,0 |
|
5,0 |
3,71 |
4,44 |
5,29 |
6,36 |
7,71 |
9,54 |
11,53 |
13,65 |
17,03 |
20,95 |
26,24 |
32,05 |
5,0 |
|
1,0 |
6,81 |
7,85 |
9,22 |
10,44 |
17,17 |
14,42 |
16,79 |
19,24 |
23,02 |
27,26 |
32,79 |
38,70 |
1,0 |
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,0 |
1,5 |
2,5 |
4,0 |
6,5 |
10,0 |
|
|
|
Приемлемые уровни качества (усиленный контроль) |
|||||||||||||
Таблица VI - Код объема выборки I
График VI - Оперативные характеристики для одноступенчатых выборочных планов контроля
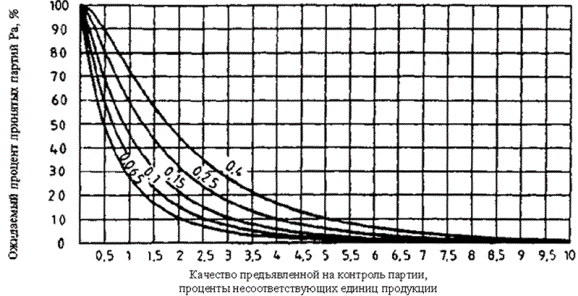

Таблица VI-1 - Табличные значения оперативных характеристик для одноступенчатых выборочных планов контроля
|
Ра |
Приемлемые уровни качества (нормальный контроль) |
Ра |
|||||||||||
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,0 |
1,5 |
2,5 |
4,0 |
6,5 |
10,0 |
||
|
99,0 |
0,02 |
0,03 |
0,04 |
0,08 |
0,14 |
0,26 |
0,44 |
0,70 |
1,33 |
2,31 |
4,12 |
6,79 |
99,0 |
|
95,0 |
0,05 |
0,08 |
0,12 |
0,20 |
0,32 |
0,56 |
0,85 |
1,28 |
2,23 |
3,61 |
5,98 |
9,27 |
95,0 |
|
90,0 |
0,09 |
0,13 |
0,19 |
0,32 |
0,48 |
0,80 |
1,19 |
1,73 |
2,89 |
4,51 |
7,21 |
10,83 |
90,0 |
|
75,0 |
0,21 |
0,30 |
0,41 |
0,64 |
0,91 |
1,42 |
2,00 |
2,78 |
4,34 |
6,39 |
9,65 |
13,82 |
75,0 |
|
50,0 |
0,50 |
0,68 |
0,89 |
1,28 |
1,73 |
2,53 |
3,39 |
4,47 |
6,54 |
9,12 |
13,00 |
17,74 |
50,0 |
|
25,0 |
1,09 |
1,42 |
1,77 |
2,41 |
3,09 |
4,25 |
5,43 |
6,87 |
9,47 |
12,57 |
17,03 |
22,27 |
25,0 |
|
10,0 |
2,05 |
2,55 |
3,08 |
3,99 |
4,93 |
6,46 |
7,97 |
9,73 |
12,81 |
16,34 |
21,24 |
26,82 |
10,0 |
|
5,0 |
2,89 |
3,52 |
4,17 |
5,26 |
6,37 |
8,14 |
9,83 |
11,78 |
15,14 |
18,89 |
24,01 |
29,75 |
5,0 |
|
1,0 |
5,17 |
6,06 |
6,97 |
8,43 |
9,85 |
12,04 |
14,08 |
16,36 |
20,14 |
24,24 |
29,66 |
35,56 |
1,0 |
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,0 |
1,5 |
2,5 |
4,0 |
6,5 |
10,0 |
|
|
|
Приемлемые уровни качества (усиленный контроль) |
|||||||||||||
Таблица VJ - Код объема выборки J
График VJ - Оперативные характеристики для одноступенчатых выборочных планов контроля

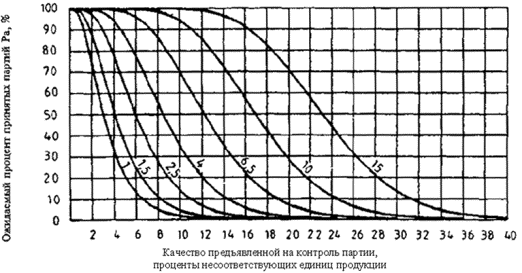
Таблица VJ-1 - Табличные значения оперативных характеристик для одноступенчатых выборочных планов контроля
|
Ра |
Приемлемые уровни качества (нормальный контроль) |
Ра |
|||||||||||
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,0 |
1,5 |
2,5 |
4,0 |
6,5 |
10,0 |
||
|
99,0 |
0,02 |
0,04 |
0,06 |
0,11 |
0,18 |
0,32 |
0,54 |
0,84 |
1,54 |
2,61 |
4,54 |
7,44 |
99,0 |
|
95,0 |
0,06 |
0,09 |
0,13 |
0,23 |
0,36 |
0,60 |
0,94 |
1,40 |
2,38 |
2,80 |
6,21 |
9,65 |
95,0 |
|
90,0 |
0,10 |
0,15 |
0,20 |
0,33 |
0,51 |
0,82 |
1,25 |
1,80 |
2,97 |
4,59 |
7,28 |
11,01 |
90,0 |
|
75,0 |
0,20 |
0,29 |
0,39 |
0,60 |
0,88 |
1,34 |
1,94 |
2,69 |
4,19 |
6,18 |
9,34 |
13,56 |
75,0 |
|
50,0 |
0,43 |
0,59 |
0,76 |
1,10 |
1,54 |
2,21 |
3,05 |
4,05 |
5,98 |
8,41 |
12,10 |
16,82 |
50,0 |
|
25,0 |
0,86 |
1,12 |
1,39 |
1,92 |
2,55 |
3,50 |
4,62 |
5,91 |
8,29 |
11,16 |
15,35 |
20,53 |
25,0 |
|
10,0 |
1,50 |
1,90 |
2,29 |
3,02 |
3,87 |
5,10 |
6,50 |
8,07 |
10,85 |
14,11 |
18,71 |
24,23 |
10,0 |
|
5,0 |
2,05 |
2,54 |
3,01 |
3,89 |
4,89 |
6,29 |
7,87 |
9,60 |
12,62 |
16,09 |
20,90 |
26,60 |
5,0 |
|
1,0 |
3,50 |
4,12 |
4,84 |
6,02 |
7,30 |
9,04 |
10,95 |
12,98 |
16,42 |
20,24 |
25,39 |
31,32 |
1,0 |
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,0 |
1,5 |
2,5 |
4,0 |
6,5 |
10,0 |
|
|
|
Приемлемые уровни качества (усиленный контроль) |
|||||||||||||
Таблица VK - Код объема выборки К
График VK - Оперативные характеристики для одноступенчатых выборочных планов контроля

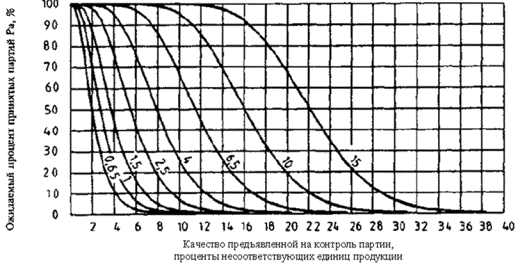
Таблица VK-1 - Табличные значения оперативных характеристик для одноступенчатых выборочных планов контроля
|
Ра |
Приемлемые уровни качества (нормальный контроль) |
Ра |
|||||||||||
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,0 |
1,5 |
2,5 |
4,0 |
6,5 |
10,0 |
||
|
99,0 |
0,03 |
0,05 |
0,08 |
0,14 |
0,23 |
0,38 |
0,64 |
0,98 |
1,74 |
2,96 |
5,03 |
8,05 |
99,0 |
|
95,0 |
0,07 |
0,10 |
0,15 |
0,26 |
0,40 |
0,64 |
1,02 |
1,49 |
2,51 |
4,04 |
6,52 |
10,00 |
95,0 |
|
90,0 |
0,10 |
0,15 |
0,21 |
0,35 |
0,54 |
0,83 |
1,29 |
1,84 |
3,01 |
4,73 |
7,44 |
11,16 |
90,0 |
|
75,0 |
0,19 |
0,27 |
0,37 |
0,58 |
0,85 |
1,26 |
1,87 |
2,59 |
4,04 |
6,08 |
9,19 |
13,31 |
75,0 |
|
50,0 |
0,35 |
0,49 |
0,65 |
0,98 |
1,37 |
1,94 |
2,76 |
3,68 |
5,48 |
7,90 |
11,45 |
16,00 |
50,0 |
|
25,0 |
0,64 |
0,86 |
1,10 |
1,58 |
2,12 |
2,89 |
3,95 |
5,11 |
7,27 |
10,09 |
14,06 |
9,01 |
25,0 |
|
10,0 |
1,06 |
1,36 |
1,70 |
2,35 |
3,07 |
4,03 |
5,33 |
6,72 |
9,23 |
12,39 |
16,72 |
21,98 |
10,0 |
|
5,0 |
1,40 |
1,77 |
2,18 |
2,94 |
3,77 |
4,87 |
6,32 |
7,84 |
10,55 |
13,92 |
18,45 |
23,88 |
5,0 |
|
1,0 |
2,29 |
2,81 |
3,36 |
4,36 |
5,42 |
6,78 |
8,52 |
10,30 |
13,39 |
17,10 |
21,97 |
27,65 |
1,0 |
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,0 |
1,5 |
2,5 |
4,0 |
6,5 |
10,0 |
|
|
|
Приемлемые уровни качества (усиленный контроль) |
|||||||||||||
Таблица VL - Код объема выборки L
График VL - Оперативные характеристики для одноступенчатых выборочных планов контроля

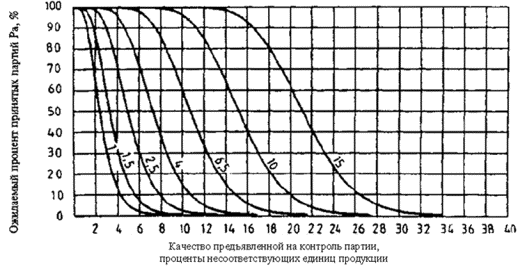
Таблица VL-1 - Табличные значения оперативных характеристик для одноступенчатых выборочных планов контроля
|
Ра |
Приемлемые уровни качества (нормальный контроль) |
Ра |
|||||||||||
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,0 |
1,5 |
2,5 |
4,0 |
6,5 |
10,0 |
||
|
99,0 |
0,04 |
0,06 |
0,09 |
0,16 |
0,27 |
0,46 |
0,73 |
1,12 |
1,95 |
3,24 |
5,52 |
8,67 |
99,0 |
|
95,0 |
0,07 |
0,11 |
0,17 |
0,27 |
0,43 |
0,70 |
1,06 |
1,58 |
2,62 |
4,18 |
6,81 |
10,34 |
95,0 |
|
90,0 |
0,10 |
0,15 |
0,22 |
0,35 |
0,55 |
0,86 |
1,29 |
1,88 |
3,05 |
4,76 |
7,59 |
11,31 |
90,0 |
|
75,0 |
0,17 |
0,24 |
0,35 |
0,53 |
0,80 |
1,21 |
1,76 |
2,49 |
3,89 |
5,86 |
9,02 |
13,08 |
75,0 |
|
50,0 |
0,29 |
0,40 |
0,56 |
0,82 |
1,19 |
1,74 |
2,43 |
3,34 |
5,02 |
7,29 |
10,84 |
15,24 |
50,0 |
|
25,0 |
0,48 |
0,65 |
0,87 |
1,23 |
1,73 |
2,44 |
3,30 |
4,41 |
6,38 |
8,97 |
12,89 |
17,62 |
25,0 |
|
10,0 |
0,74 |
0,97 |
1,27 |
1,74 |
2,37 |
3,24 |
4,28 |
5,58 |
7,82 |
10,70 |
14,94 |
19,95 |
10,0 |
|
5,0 |
0,95 |
1,23 |
1,57 |
2,12 |
2,84 |
3,82 |
4,97 |
6,38 |
8,79 |
11,84 |
16,26 |
21,42 |
5,0 |
|
1,0 |
1,47 |
1,84 |
2,30 |
3,01 |
3,91 |
5,10 |
6,47 |
8,11 |
10,84 |
14,19 |
18,93 |
24,34 |
1,0 |
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,0 |
1,5 |
2,5 |
4,0 |
6,5 |
10,0 |
|
|
|
Приемлемые уровни качества (усиленный контроль) |
|||||||||||||
Таблица VM - Код объема выборки М
График VM - Оперативные характеристики для одноступенчатых выборочных планов контроля

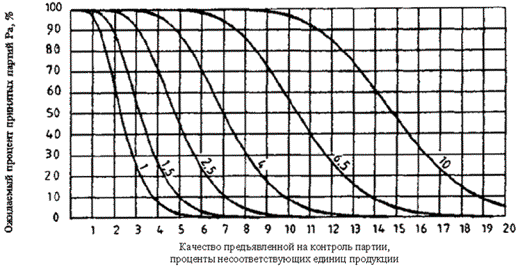
Таблица VM-1 - Табличные значения оперативных характеристик для одноступенчатых выборочных планов контроля
|
Ра |
Приемлемые уровни качества (нормальный контроль) |
Ра |
|||||||||||
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,0 |
1,5 |
2,5 |
4,0 |
6,5 |
10,0 |
||
|
99,0 |
0,05 |
0,07 |
0,11 |
0,19 |
0,31 |
0,52 |
0,81 |
1,24 |
2,12 |
3,46 |
5,81 |
9,03 |
99,0 |
|
95,0 |
0,08 |
0,12 |
0,18 |
0,29 |
0,47 |
0,74 |
1,12 |
1,66 |
2,73 |
4,31 |
6,97 |
10,51 |
95,0 |
|
90,0 |
0,10 |
0,15 |
0,22 |
0,37 |
0,57 |
0,89 |
1,33 |
1,93 |
3,11 |
4,82 |
7,65 |
11,36 |
90,0 |
|
75,0 |
0,16 |
0,23 |
0,33 |
0,53 |
0,79 |
1,20 |
1,74 |
2,46 |
3,84 |
5,78 |
8,90 |
12,90 |
75,0 |
|
50,0 |
0,26 |
0,23 |
0,51 |
0,77 |
1,12 |
1,64 |
2,31 |
3,18 |
4,80 |
7,00 |
10,45 |
14,75 |
50,0 |
|
25,0 |
0,41 |
0,37 |
0,75 |
1,11 |
1,56 |
2,22 |
3,02 |
4,07 |
5,93 |
8,41 |
12,18 |
16,78 |
25,0 |
|
10,0 |
0,61 |
0,56 |
1,05 |
1,50 |
2,06 |
2,86 |
3,81 |
5,01 |
7,11 |
9,84 |
13,89 |
18,73 |
10,0 |
|
5,0 |
0,75 |
0,80 |
1,28 |
1,79 |
2,43 |
3,31 |
4,35 |
5,65 |
7,89 |
10,77 |
14,99 |
19,97 |
5,0 |
|
1,0 |
1,12 |
0,99 |
1,81 |
2,46 |
3,24 |
4,30 |
5,52 |
7,02 |
9,53 |
12,68 |
17,19 |
22,41 |
1,0 |
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,0 |
1,5 |
2,5 |
4,0 |
6,5 |
10,0 |
|
|
|
Приемлемые уровни качества (усиленный контроль) |
|||||||||||||
Таблица VN - Код объема выборки N
График VN - Оперативные характеристики для одноступенчатых выборочных планов контроля
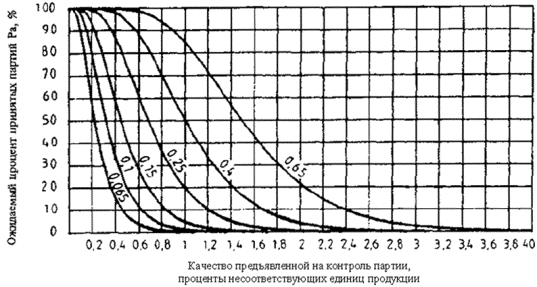
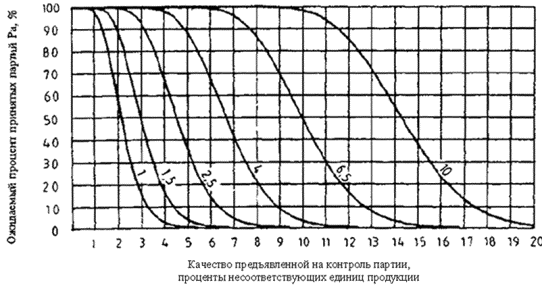
Таблица VN-1 - Табличные значения оперативных характеристик для одноступенчатых выборочных планов контроля
|
Ра |
Приемлемые уровни качества (нормальный контроль) |
Ра |
|||||||||||
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,0 |
1,5 |
2,5 |
4,0 |
6,5 |
10,0 |
||
|
99,0 |
0,05 |
0,08 |
0,13 |
0,22 |
0,35 |
0,57 |
0,91 |
1,36 |
2,29 |
3,69 |
6,10 |
9,55 |
99,0 |
|
95,0 |
0,08 |
0,13 |
0,19 |
0,31 |
0,48 |
0,77 |
1,18 |
1,73 |
2,82 |
4,41 |
7,07 |
10,80 |
95,0 |
|
90,0 |
0,11 |
0,16 |
0,24 |
0,37 |
0,57 |
0,89 |
1,35 |
1,96 |
3,13 |
4,84 |
7,64 |
11,51 |
90,0 |
|
75,0 |
0,15 |
0,22 |
0,33 |
0,50 |
0,75 |
1,14 |
1,69 |
2,39 |
3,73 |
5,62 |
8,66 |
12,77 |
75,0 |
|
50,0 |
0,23 |
0,32 |
0,46 |
0,69 |
1,00 |
1,48 |
2,14 |
2,96 |
4,49 |
6,59 |
9,90 |
14,28 |
50,0 |
|
25,0 |
0,34 |
0,46 |
0,64 |
0,93 |
1,32 |
1,90 |
2,68 |
3,64 |
5,36 |
7,69 |
11,26 |
15,89 |
25,0 |
|
10,0 |
0,46 |
0,62 |
0,85 |
1,21 |
1,68 |
2,36 |
3,26 |
4,34 |
6,26 |
8,78 |
11,58 |
17,44 |
10,0 |
|
5,0 |
0,56 |
0,74 |
1,00 |
1,40 |
1,93 |
2,68 |
3,65 |
4,81 |
6,84 |
9,48 |
13,43 |
18,40 |
5,0 |
|
1,0 |
0,79 |
1,03 |
1,35 |
1,84 |
2,48 |
3,36 |
4,48 |
5,79 |
8,04 |
10,91 |
15,11 |
20,31 |
1,0 |
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,0 |
1,5 |
2,5 |
4,0 |
6,5 |
10,0 |
|
|
|
Приемлемые уровни качества (усиленный контроль) |
|||||||||||||
Таблица VP - Код объема выборки Р
График VP - Оперативные характеристики для одноступенчатых выборочных планов контроля
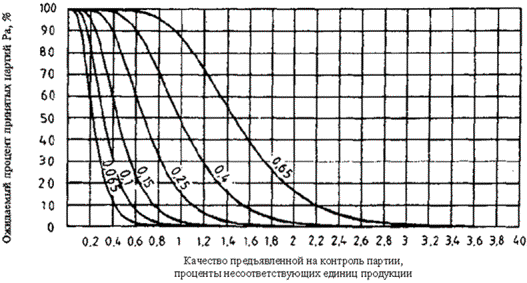

Таблица VP-1 - Табличные значения оперативных характеристик для одноступенчатых выборочных планов контроля
|
Ра |
Приемлемые уровни качества (нормальный контроль) |
Ра |
|||||||||||
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,0 |
1,5 |
2,5 |
4,0 |
6,5 |
10,0 |
||
|
99,0 |
0,064 |
0,101 |
0,150 |
0,254 |
0,405 |
0,65 |
0,99 |
1,52 |
2,52 |
4,00 |
6,52 |
10,00 |
99,0 |
|
95,0 |
0,094 |
0,143 |
0,210 |
0,344 |
0,534 |
0,84 |
1,25 |
1,86 |
3,00 |
4,66 |
7,40 |
11,22 |
95,0 |
|
90,0 |
0,114 |
0,173 |
0,249 |
0,402 |
0,617 |
0,95 |
1,40 |
2,07 |
3,29 |
5,04 |
7,91 |
11,85 |
90,0 |
|
75,0 |
0,157 |
0,233 |
0,330 |
0,519 |
0,779 |
1,18 |
1,70 |
2,46 |
3,82 |
5,73 |
8,80 |
12,96 |
75,0 |
|
50,0 |
0,222 |
0,321 |
0,445 |
0,683 |
1,000 |
1,48 |
2,08 |
2,96 |
4,48 |
6,58 |
9,88 |
14,27 |
50,0 |
|
25,0 |
0,309 |
0,437 |
0,594 |
0,889 |
1,272 |
1,83 |
2,54 |
3,53 |
5,23 |
7,52 |
11,05 |
15,66 |
25,0 |
|
10,0 |
0,411 |
0,571 |
0,763 |
1,116 |
1,567 |
2,22 |
3,02 |
4,12 |
5,98 |
8,45 |
12,19 |
16,98 |
10,0 |
|
5,0 |
0,485 |
0,666 |
0,882 |
1,275 |
1,770 |
2,47 |
3,33 |
4,51 |
5,47 |
9,04 |
12,90 |
17,80 |
5,0 |
|
1,0 |
0,657 |
0,884 |
1,150 |
1,621 |
2,206 |
3,02 |
4,00 |
5,32 |
7,46 |
10,23 |
14,31 |
19,41 |
1,0 |
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,0 |
1,5 |
2,5 |
4,0 |
6,5 |
10,0 |
|
|
|
Приемлемые уровни качества (усиленный контроль) |
|||||||||||||
Таблица VIA - Соответствие между планами усиленного и нормального контроля
|
AQL 2) |
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,0 |
1,5 |
2,5 |
4,0 |
6,5 |
10,0 |
|
В1) |
|
|
|
|
|
|
|
C-1,5 |
B-2,5 |
B-4,0 |
B-6,5 |
|
С |
|
|
|
|
|
D-0,65 |
С-1,0 |
C-1,5 |
C-2,5 |
C-4,0 |
C-6,5 |
|
D |
|
|
|
|
Е-0,40 |
D-0,65 |
D-1,0 |
D-1,5 |
D-2,5 |
D-4,0 |
D-6,5 |
|
Е |
|
|
F-0,15 |
Е-0,25 |
Е-0,40 |
Е-0,65 |
Е-1,0 |
E-1,5 |
E-2,5 |
E-4,0 |
E-6,5 |
|
F |
|
G-0,10 |
F-0,15 |
F-0,25 |
F-0,40 |
F-0,65 |
F-l,0 |
F-1,5 |
F-2,5 |
F-4,0 |
F-6,5 |
|
G |
G-0,065 |
G-0,10 |
G-0,15 |
G-0,25 |
G-0,40 |
G-0,65 |
G-1,0 |
G-1,5 |
G-2,5 |
G-4,0 |
G-6,5 |
|
Н |
Н-0,065 |
Н-0,10 |
Н-0,15 |
Н-0,25 |
Н-0,40 |
H-0,65 |
H-1,0 |
H-1,5 |
H-2,5 |
H-4,0 |
H-6,5 |
|
I |
I-0,065 |
I-0,10 |
I-0,15 |
I-0,25 |
I-0,40 |
I-0,65 |
I-1,0 |
I-1,5 |
I-2,5 |
1-4,0 |
I-6,5 |
|
J |
J-0,065 |
J-0,10 |
J-0,15 |
J-0,25 |
J-0,40 |
J-0,65 |
J-1,0 |
J-1,5 |
J-2,5 |
J-4,0 |
J-6,5 |
|
К |
К-0,065 |
К-0,10 |
К-0,15 |
К-0,25 |
К-0,40 |
K-0,65 |
K-1,0 |
K-1,5 |
K-2,5 |
K-4,0 |
K-6,5 |
|
L |
L-0,065 |
L-0,10 |
L-0,15 |
L-0,25 |
L-0,40 |
L-0,65 |
L-1,0 |
L-1,5 |
L-2,5 |
L-4,0 |
L-6,5 |
|
М |
М-0,065 |
М-0,10 |
М-0,15 |
М-0,25 |
М-0,40 |
M-0,65 |
M-1,0 |
M-1,5 |
M-2,5 |
M-4,0 |
M-6,5 |
|
N |
N-0,065 |
N-0,10 |
N-0,15 |
N-0,25 |
N-0,40 |
N-0,65 |
N-1,0 |
N-1,5 |
N-2,5 |
N-4,0 |
N-6,5 |
|
Р |
Р-0,065 |
Р-0,10 |
Р-0,15 |
Р-0,25 |
Р-0,40 |
P-0,65 |
P-1,0 |
P-1,5 |
P-2,5 |
P-4,0 |
P-6,5 |
|
1) Только для s-метода. 2) Код объема выборки. Примечание - Таблица устанавливает связь между кодом объема выборки (слева) и AQL (сверху) для плана контроля выше нормального. Таблица дает возможность код объема выборки и AQL для нормального контроля использовать для усиленного контроля. |
|||||||||||
Таблица VIB - Соответствие между планами ослабленного и нормального контроля
|
AQL 2) |
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,0 |
1,5 |
2,5 |
4,0 |
6,5 |
10,0 |
|
В1) |
|
|
|
|
|
|
|
B-4,0 |
B-6,5 |
B-10,0 |
B-15,0 |
|
С |
|
|
|
|
|
C-1,5 |
B-2,5 |
B-4,0 |
B-6,5 |
B-10,0 |
B-15,0 |
|
D |
|
|
|
|
C-1,0 |
C-1,5 |
B-2,5 |
B-4,0 |
B-6,5 |
B-10,0 |
B-15,0 |
|
Е |
|
|
Е-0,40 |
D-0,65 |
C-1,0 |
C-1,5 |
B-2,5 |
B-4,0 |
B-6,5 |
B-10,0 |
B-15,0 |
|
F |
|
Е-0,25 |
Е-0,40 |
D-0,65 |
C-1,0 |
C-1,5 |
C-2,5 |
C-4,0 |
C-6,5 |
C-10,0 |
C-15,0 |
|
G |
F-0,15 |
Е-0,25 |
Е-0,40 |
D-0,65 |
D-1,0 |
D-1,5 |
D-2,5 |
D-4,0 |
D-6,5 |
D-10,0 |
D-15,0 |
|
Н |
F-0,15 |
Е-0,25 |
Е-0,40 |
E-0,65 |
E-1,0 |
E-1,5 |
E-2,5 |
E-4,0 |
E-6,5 |
E-10,0 |
E-15,0 |
|
I |
F-0,15 |
F-0,25 |
F-0,40 |
F-0,65 |
F-1,0 |
F-1,5 |
F-2,5 |
F-4,0 |
F-6,5 |
F-10,0 |
F-15,0 |
|
J |
G-0,15 |
G-0,25 |
G-0,40 |
G-0,65 |
G-1,0 |
G-1,5 |
G-2,5 |
G-4,0 |
G-6,5 |
G-10,0 |
G-15,0 |
|
К |
Н-0,15 |
Н-0,25 |
Н-0,40 |
H-0,65 |
H-1,0 |
H-1,5 |
H-2,5 |
H-4,0 |
H-6,5 |
H-10,0 |
H-15,0 |
|
L |
I-0,15 |
I-0,25 |
I-0,40 |
I-0,65 |
I-1,0 |
I-1,5 |
I-2,5 |
I-4,0 |
I-6,5 |
1-10,0 |
I-15,0 |
|
М |
J-0,15 |
J-0,25 |
J-0,40 |
J-0,65 |
J-1,0 |
J-1,5 |
J-2,5 |
J-4,0 |
J-6,5 |
J-10,0 |
J-15,0 |
|
N |
К-0,15 |
К-0,25 |
К-0,40 |
K-0,65 |
K-1,0 |
K-1,5 |
K-2,5 |
K-4,0 |
K-6,5 |
N-10,0 |
K-15,0 |
|
Р |
L-0,15 |
L-0,25 |
L-0,40 |
L-0,65 |
L-1,0 |
L-1,5 |
L-2,5 |
L-4,0 |
L-6,5 |
P-10,0 |
L-15,0 |
|
1) Только для s-метода. 2) Код объема выборки. Примечание - Таблица устанавливает связь между кодом объема выборки (слева) и AQL (сверху) для плана контроля выше нормального. Таблица дает возможность код объема выборки и AQL для нормального контроля использовать для ослабленного контроля. |
|||||||||||
Диаграмма А - Коды объема выборок стандартных планов выборочного контроля с установленным уровнем качества и вероятностью приемки 95 % и 10 %

Диаграмма s-D - Кривые приемки для предельных значений с общим уровнем качества: s-метод для кода объема выборки D (объем выборки - 5)

Диаграмма s-E - Кривые приемки для предельных значений с общим уровнем качества: s-метод для кода объема выборки Е (объем выборки - 7)

Диаграмма s-F - Кривые приемки для предельных значений с общим уровнем качества: s-метод для кода объема выборки F (объем выборки - 10)
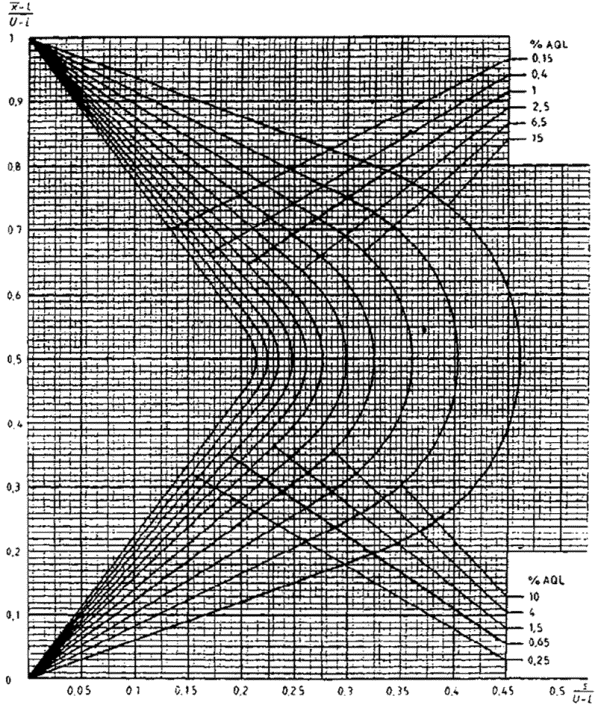
Диаграмма s-G - Кривые приемки для предельных значений с общим уровнем качества: s-метод для кода объема выборки G (объем выборки - 15)

Диаграмма s-H - Кривые приемки для предельных значений с общим уровнем качества: s-метод для кода объема выборки Н (объем выборки - 20)
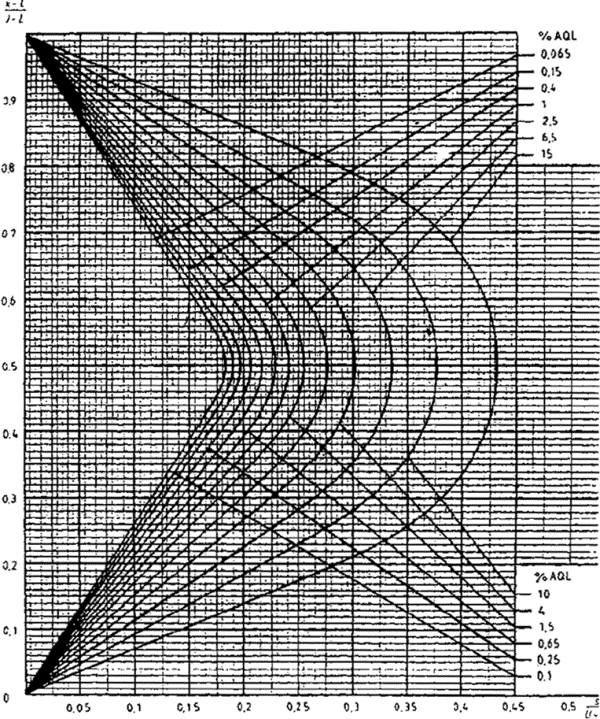
Диаграмма s-I - Кривые приемки для предельных значений с общим уровнем качества: s-метод для кода объема выборки I (объем выборки - 25)

Диаграмма s-J - Кривые приемки для предельных значений с общим уровнем качества: s-метод для кода объема выборки J (объем выборки - 35)

Диаграмма s-K - Кривые приемки для предельных значений с общим уровнем качества: s-метод для кода объема выборки К (объем выборки - 50)

Диаграмма s-L - Кривые приемки для предельных значений с общим уровнем качества: s-метод для кода объема выборки L (объем выборки - 75)
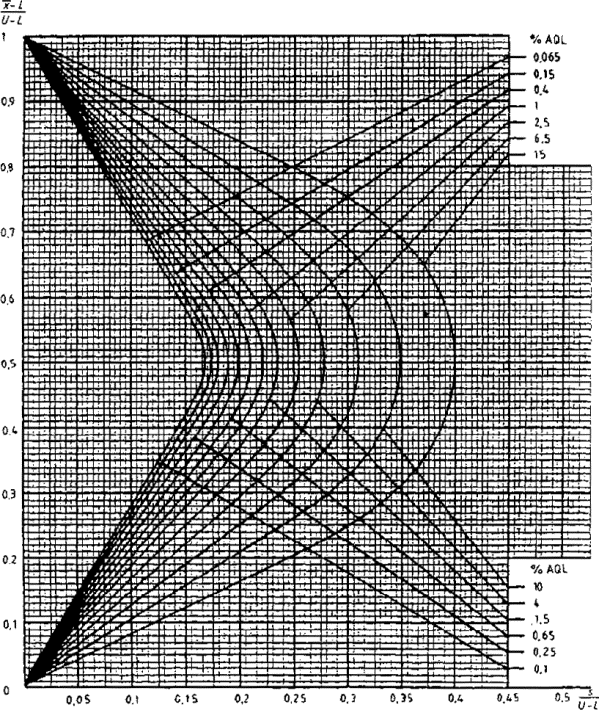
Диаграмма s-M - Кривые приемки для предельных значений с общим уровнем качества: s-метод для кода объема выборки М (объем выборки - 100)
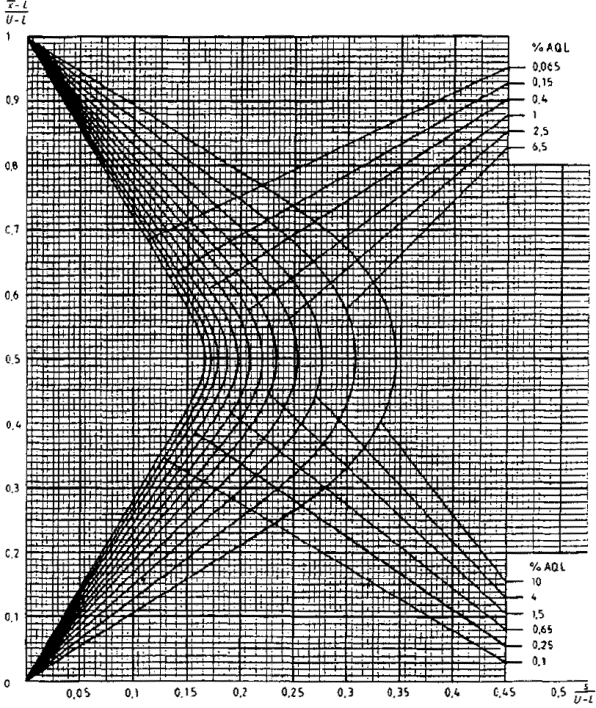
Диаграмма s-N - Кривые приемки для предельных значений с общим уровнем качества: s-метод для кода объема выборки N (объем выборки - 150)
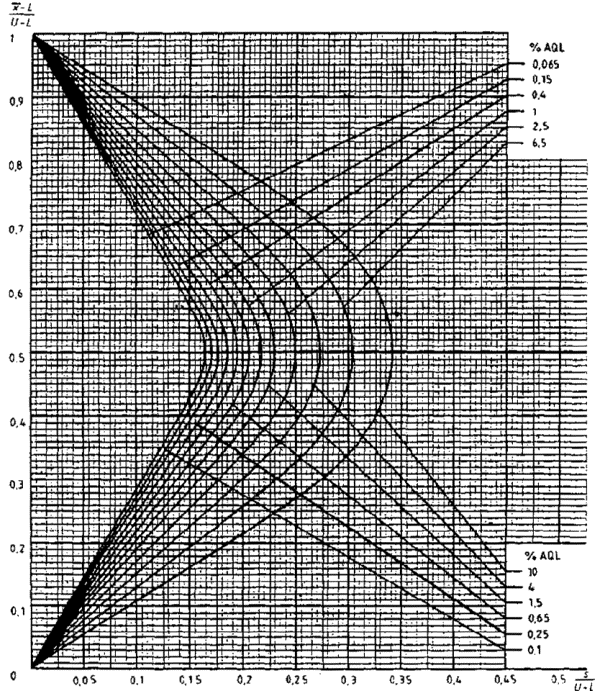
Диаграмма s-P - Кривые приемки для предельных значений с общим уровнем качества: s-метод для кода объема выборки Р (объем выборки - 200)

Диаграмма s-С - Кривые приемки для предельных значений с общим уровнем качества: s-метод для кода объема выборки С
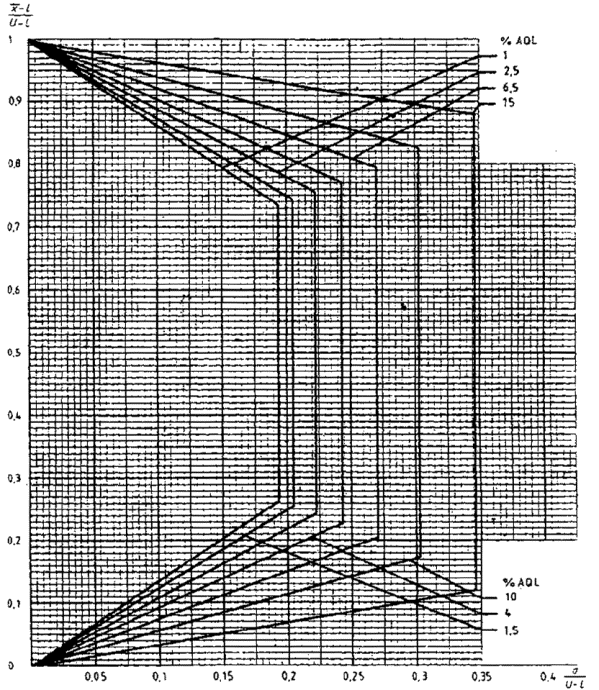
Диаграмма s-D - Кривые приемки для предельных значений с общим уровнем качества: s-метод для кода объема выборки D

Диаграмма s-Е - Кривые приемки для предельных значений с общим уровнем качества: s-метод для кода объема выборки Е
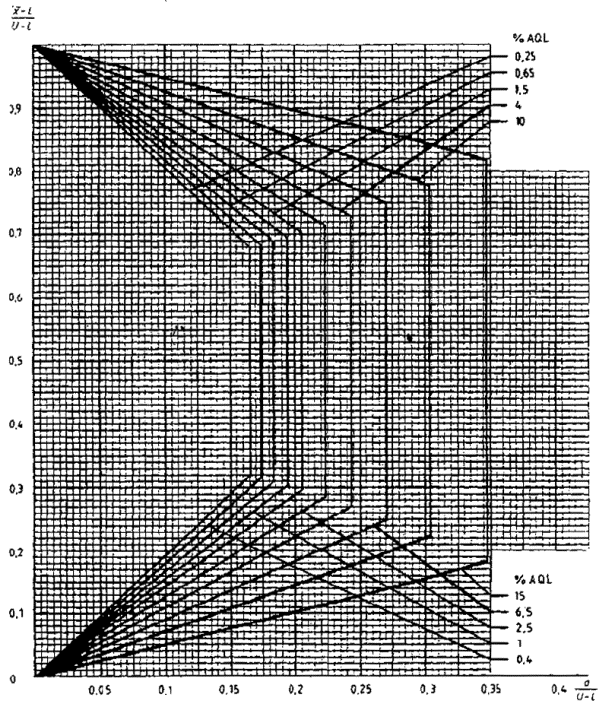
Диаграмма s-F - Кривые приемки для предельных значений с общим уровнем качества: s-метод для кода объема выборки F
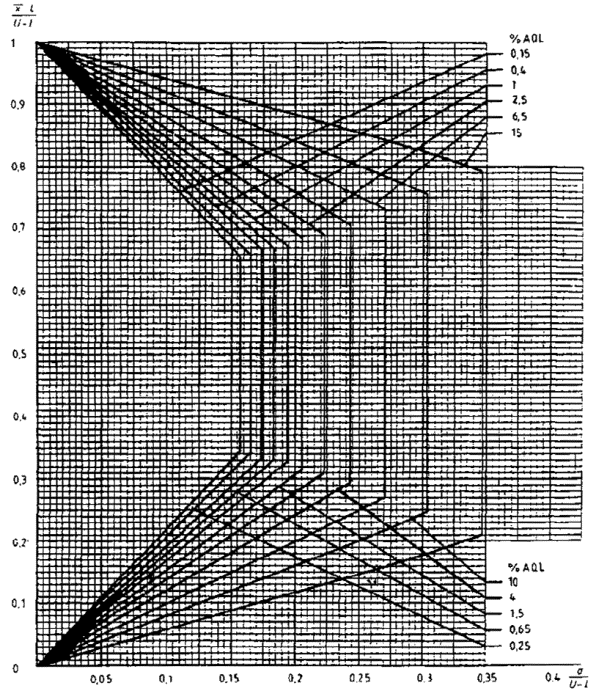
Диаграмма s-G - Кривые приемки для предельных значений с общим уровнем качества: s-метод для кода
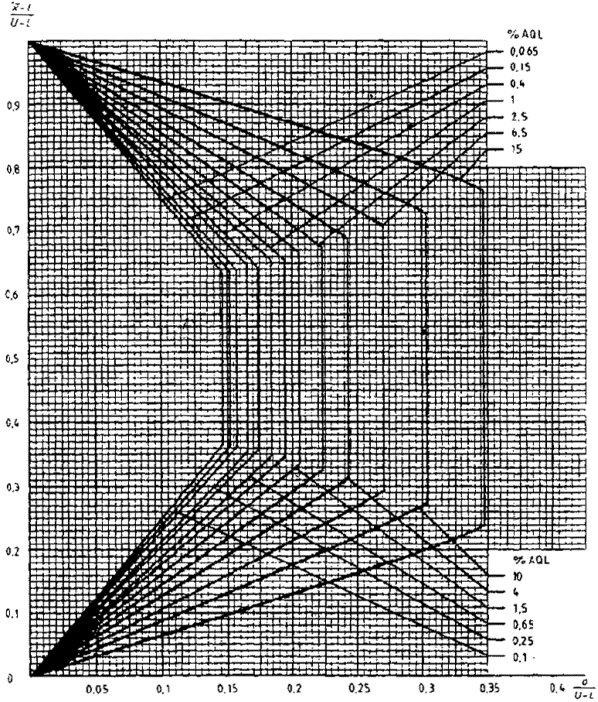
Диаграмма s-Н - Кривые приемки для предельных значений с общим уровнем качества: s-метод для кода объема выборки Н

Диаграмма s-I - Кривые приемки для предельных значений с общим уровнем качества: s-метод для кода объема выборки I
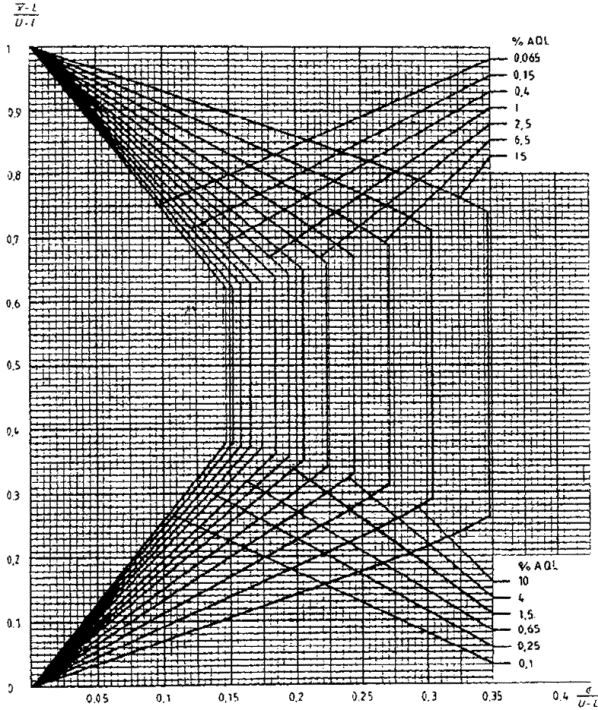
Диаграмма s-J - Кривые приемки для предельных значений с общим уровнем качества: a-метод для кода объема выборки J

Диаграмма s-К - Кривые приемки для предельных значений с общим уровнем качества: s-метод для кода объема выборки К

Диаграмма s-L - Кривые приемки для предельных значений с общим уровнем качества: s-метод для кода объема выборки L
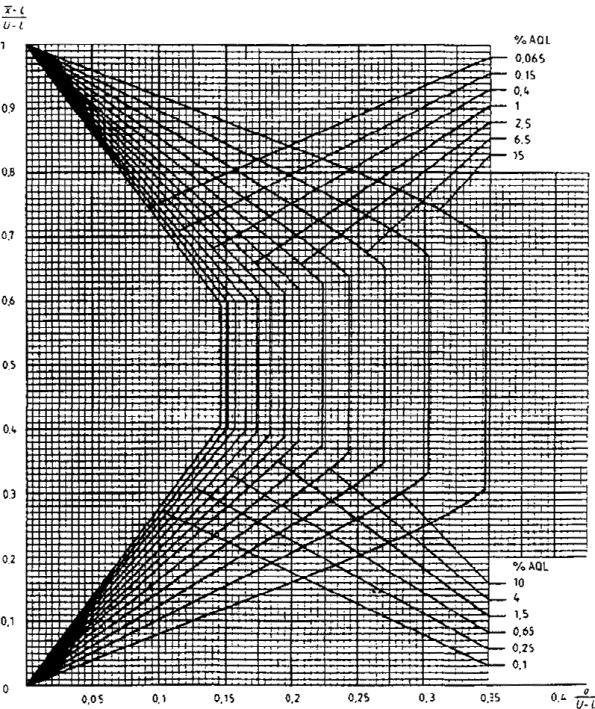
Диаграмма s-М - Кривые приемки для предельных значений с общим уровнем качества: s-метод для кода объема выборки М
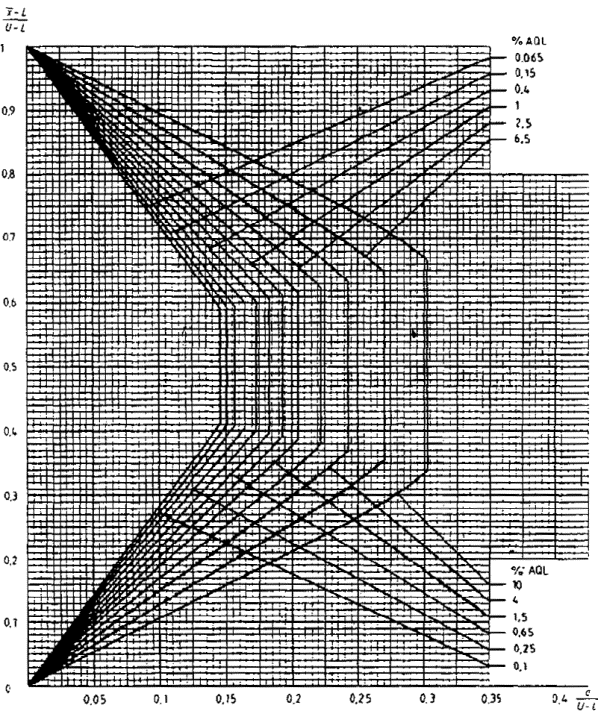
Диаграмма s-N - Кривые приемки для предельных значений с общим уровнем качества: s-метод для кода объема выборки N

Диаграмма s-Р - Кривые приемки для предельных значений с общим уровнем качества: s-метод для кода объема выборки Р

ПРИЛОЖЕНИЕ А
(обязательное)
Процедуры получения s и s
А.1 Процедуры получения s
А.1.1 Оценка стандартного отклонения партии по выборке обозначается символом s. Значение величины рассчитывают по формуле
 ,
,
где хi - измеренное значение характеристики i-й единицы в выборке объемом п изделий;
![]() - среднее арифметическое значений хi, то есть:
- среднее арифметическое значений хi, то есть:
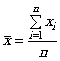 .
.
А.1.2 Приведенная выше формула расчета s не рекомендуется для вычисления, так как расчеты можно упростить путем вычитания из хi произвольного целого числа а и использования следующей эквивалентной формулы:
![]() .
.
Пример - Возьмем измерения, приведенные в примере к 14.6 настоящего стандарта. Принимаем а - 65 и представляем расчеты в виде таблицы:
|
xi |
а |
(xi-а) |
(xi-а)2 |
|
63,5 |
65 |
-1,5 |
2,25 |
|
62,0 |
65 |
-3,0 |
9,00 |
|
65,2 |
65 |
0,2 |
0,04 |
|
61,7 |
65 |
-3,3 |
10,89 |
|
69,0 |
65 |
4,0 |
16,00 |
|
67,1 |
65 |
2,1 |
4,41 |
|
60,0 |
65 |
-5,0 |
25,00 |
|
66,4 |
65 |
1,4 |
1,96 |
|
62,8 |
65 |
-2,2 |
4,84 |
|
68,0 |
65 |
3,0 |
9,00 |
|
Sxi=645,7 |
|
|
S(xi-a)2=83,39 |
|
n=10 |
|
|
S(xi-a)2-n(a- |
|
|
|
|
(n-1)s2=81,54 |
|
a=65 |
|
|
(n-1)=9 |
|
(a- |
|
|
s2=9,06 |
|
(a- |
|
|
s=3,01 |
|
n(a- |
|
|
|
А.1.3 При наличии калькулятора величину а в А.1.2 можно принять равной нулю, тогда формула приобретет вид:
![]()
На персональном компьютере можно одновременно получить кумулятивную сумму и для и для (хi)2, так что нет необходимости записывать отдельные значения хi и (х)2. Но в следующем примере эти значения приведены для того, чтобы проиллюстрировать процесс. Заметьте, какими большими могут стать числа в четвертом столбце, и при использовании электронного калькулятора убедитесь, что он не отбрасывает цифры. Данные взяты из примера, приведенного в С.9.2.5 приложения С. Далее необходимо рассчитать s.
|
хi |
Кумулятивная сумма хi |
|
Кумулятивная
сумма |
|
515 |
515 |
265225 |
265225 |
|
491 |
1006 |
241081 |
506306 |
|
479 |
1485 |
229441 |
735747 |
|
507 |
1992 |
257049 |
992796 |
|
543 |
2535 |
294849 |
1287645 |
|
521 |
3056 |
271441 |
1559086 |
|
536 |
3592 |
287296 |
1846382 |
|
483 |
4075 |
233289 |
2079671 |
|
509 |
4584 |
259081 |
2338752 |
|
514 |
5098 |
264196 |
2602948 |
|
507 |
5605 |
257049 |
2859997 |
|
484 |
6089 |
234256 |
3094253 |
|
526 |
6615 |
276676 |
3370929 |
|
552 |
7167 |
304704 |
3675633 |
|
499 |
7666 |
249001 |
3924634 |
|
530 |
8196 |
280900 |
4205534 |
|
512 |
8708 |
262144 |
4467678 |
|
492 |
9200 |
242064 |
4709742 |
|
521 |
9721 |
271441 |
4981183 |
|
467 |
10188 |
218089 |
5199272 |
|
489 |
10677 |
239121 |
5438393 |
|
513 |
11190 |
263169 |
5701562 |
|
535 |
11725 |
286225 |
5987787 |
|
501 |
12226 |
251001 |
6238788 |
|
529 |
12755 |
279841 |
6518629 |
|
|
|
|
|
|
n=25 |
|
|
|
|
|
|
|
|
|
|
|
n-1=24 |
|
|
|
|
s2=459,5 |
|
|
|
|
s=21,43 |
|
Таким
образом, среднее ![]() =510,2, а оценка стандартного отклонения партии s=21,43.
=510,2, а оценка стандартного отклонения партии s=21,43.
A.1.4 Если изменения показаний измерительного прибора
невелики, можно упростить арифметические вычисления, принимая в расчет только
ту часть измерения, которая изменяется от изделия к изделию; например, если хi - имеет значения 27,515; 27,491; 27,479 и т.д., их
следует учитывать, как если бы хi был равен 515; 491; 479 и т.д. Поставив эти цифры в
предыдущий пример, получаем ![]() =27,510 и s=0,021.
=27,510 и s=0,021.
А.1.5 Уравнению для s можно придать и другие формы. В зависимости от типа калькулятора можно использовать одну из следующих формул:

или
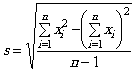
А.2 Процедура получения s
А.2.1 Если окажется, что значения s (или ![]() ) находятся в состоянии статистической управляемости, можно
предположить, что s- это корень из среднего значения квадрата s (среднее взвешенное) (или
) находятся в состоянии статистической управляемости, можно
предположить, что s- это корень из среднего значения квадрата s (среднее взвешенное) (или ![]() /c), получим
/c), получим

где l- число партий;
пi - объем выборки из i-й партии;
si - значение выборочного стандартного отклонения для i-й партии.
A.2.2 Если объем выборки для каждой партии один и тот же, то вышеприведенная формула сводится к следующей:

А.2.3 В случае R-метода величина ![]() в вышеприведенных
выражениях должна быть заменена на (
в вышеприведенных
выражениях должна быть заменена на (![]() /ci)2,
где
/ci)2,
где ![]() - средний размах; сi - коэффициент масштаба для выборки из i-й партии.
- средний размах; сi - коэффициент масштаба для выборки из i-й партии.
ПРИЛОЖЕНИЕ В
(обязательное)
Теоретическое обоснование
В.0 Символы
В данном приложении используются следующие обозначения:
Р - общий процент или доля несоответствующих единиц продукции для процесса:
p=pU+pL
pL - процент несоответствующих единиц, выходящий за нижний предел поля допуска;
pU - процент несоответствующих единиц, выходящий за верхний предел поля допуска;
Р - функция распределения;
Q - параметр качества, равный zU минус zL;
z - нормированное значение:
![]()
zL - значение z для нижнего предела поля допуска:
![]()
zU - значение z для верхнего предела поля допуска:
![]()
B.1 Нормальное распределение
В.1.1 Статистическая теория, на основе которой рассчитываются риски при контроле по количественному признаку, основана на свойствах нормального распределения, поэтому настоящий стандарт применим только там, где есть основание считать, что распределение измеряемой характеристики нормальное или близкое к нормальному.
В.1.2 Нормальное распределение можно полностью определить через среднее m и стандартное отклонение с генеральной совокупности; если эти два параметра известны, можно рассчитать вероятность, с которой любое измеренное значение х попадет между двумя заданными значениями, а также вероятность, с которой любое измеренное значение выходит за установленные значения для верхнего или нижнего предела (рисунок 5).

Рисунок 5 - Нормальное распределение
В.1.3 Чтобы облегчить сведение в таблицу этих вероятностей, измеренные значения х преобразуют в нормированную величину z:
![]() .
.
Такой прием приводит все кривые нормального распределения к общему виду (рисунок 6), упрощает уравнение такой кривой и, поскольку общая площадь под кривой равна 1, позволяет построить одну таблицу, которая для данного значения z дает значение Р интегральной функции плотности вероятности нормального распределения (незаштрихованная площадь под кривой).

Рисунок 6 - Стандартное нормальное распределение
В.2 Доля несоответствующих единиц продукции
В.2.1 Доля несоответствующих единиц продукции представляет собой область (или области) под кривой функции распределения, находящуюся за пределом (или пределами) поля допуска.
Примечание - Долю несоответствующих единиц продукции на практике часто выражают в процентах (см. разделы 1-4).
В.2.2 Если распределение х нормальное, среднее m и стандартное отклонение s известны, то долю несоответствующих единиц р относительно заданных пределов характеристики L и(или) U можно определить по таблицам для нормального распределения как рU=1-РU и pL=pL (см. рисунок 7).

Рисунок 7 - Доля несоответствующих единиц продукции для постоянного s=1 и различных значений среднего (m1, m2, m3) по отношению к заданному нижнему пределу поля допуска характеристики качества
В.3 Параметр качества
В.3.1 Преобразовав исходное нормальное распределение к распределению с параметрами m=0, s=1, получим, что доля несоответствующих единиц однозначно определяется величиной
![]() .
.
В.3.2 Параметр качества для предельного значения поля допуска, полученный подобным образом, может быть использован в приемочном контроле вместо доли несоответствующих единиц продукции. Для верхнего предела поля допуска U параметр качества qU определяется по формуле
![]() ,
,
и для нижнего предела поля допуска L параметр качества qL определяется по формуле
![]() .
.
В.4 Область приемлемости для односторонних и двусторонних пределов поля допуска
При рассмотрении непрерывной серии партий AQL- это уровень качества, который при выборочном контроле служит границей удовлетворительного среднего уровня качества процесса и выражается в процентах несоответствующих изделий.
При рассмотрении одностороннего или двустороннего допуска можно установить связь AQL с параметром качества q. Так как существует взаимооднозначное соответствие между областью вне пределов поля допуска и параметром качества, можно ввести контрольный норматив K как нижнюю границу параметра качества q - приемлемости процесса при приемочном контроле, то есть процесс приемлем, если q³K.
Таким образом задается:
- альтернативный показатель AQL;
- значение константы K.
Для заданного множества значений пределов поля допуска pL или pU, зависящих от m и s на плоскости в координатах (m, s) должна быть область, где pL (или рU) меньше или равно AQL, которая является зоной приемлемости процессов. И наоборот, должна быть другая область, где pL (или pU) больше AQL, которая является зоной неприемлемости. Эти области можно разделить одной прямой линией.
Для нижнего одностороннего предела допуска график AQL в координатах (m, s) задается зависимостью
![]()
или
![]() .
.
Для всех точек плоскости выше этой прямой средний процент несоответствующих единиц продукции меньше или равен AQL и, следовательно, процесс приемлем. Для точек ниже этой прямой он больше AQL и, следовательно, процесс неприемлем (рисунок 8).
Для верхнего одностороннего предела поля допуска могут быть получены аналогичные соотношения:
![]()
или
![]()
Для точек, расположенных под этой линией, средний процент несоответствующих единиц процесса меньше AQL и, следовательно, процесс приемлем, над этой линией - неприемлем (рисунок 9).
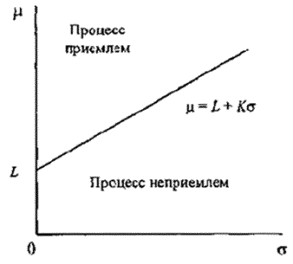
Рисунок 8 - Приемочная карта для нижнего предела поля допуска (s и m известны)
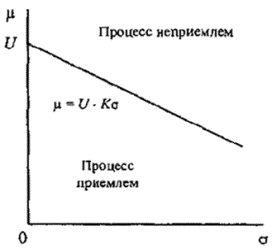
Рисунок 9 - Приемочная карта для верхнего предела поля допуска (s и m известны)
Двустороннему допуску соответствует рисунок 10.
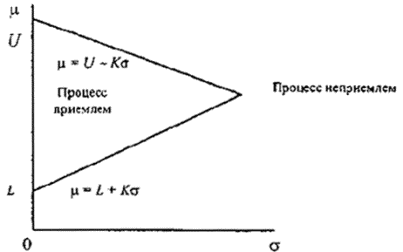
Рисунок 10 - Приемочная карта для двустороннего допуска (s и m известны)
В.5 Область приемлемости для предельных значений с общим уровнем качества
В.5.1 Пределы двустороннего допуска с общим AQL
Если заданы верхнее и нижнее предельные значения с общим уровнем качества, допуск называется двусторонним допуском с общим уровнем качества. Задание общего уровня качества не позволяет отдельно получить доли несоответствующих единиц продукции рU и pL для верхнего и нижнего пределов поля допуска. Вместо этого устанавливают их сумму р, которая не должна быть превышена.
Иначе не существует способа получить график зависимости одного параметра, такого как K, соответствующего AQL. Вместо этого для нахождения пары значений (m, s), для которой доля несоответствующих единиц равна AQL, следует использовать математическое соотношение между величинами m и s и общей долей несоответствующих единиц процесса.
Для данного значения s не только рU и pL зависят от m, но и их сумма рU+pL=p также зависит от значения m относительно U и L (рисунок 11). Значение p достигает минимума, когда m находится посередине между U и L, и возрастает, когда m отклоняется от середины.
Площадь под кривой, находящаяся за пределами поля допуска для данной функции распределения при фиксированном значении m определяется величиной s (рисунок 12).
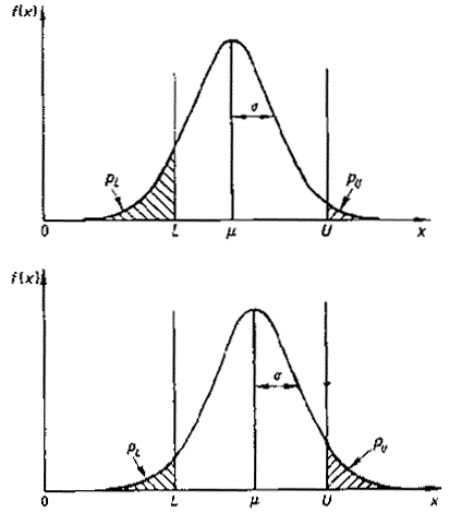
Рисунок 11 - Влияние изменения m на долю несоответствующих единиц процесса (при постоянном значении s)

Рисунок 12 - Влияние изменения s (при постоянном m) на долю несоответствия процесса
В.5.2 Максимальное стандартное отклонение процесса (MPSD)
Наибольшее значение s, которое возможно при данном AQL и m, расположенном посередине между U и L, можно рассматривать как максимальное стандартное отклонение процесса (MPSD) при нормальном контроле. Если s процесса больше значения этой величины, то доля несоответствующих единиц продукции в этом процессе больше AQL. Но обратное утверждение не всегда верно.
При усиленном или ослабленном контроле MPSD - это максимальное стандартное отклонение процесса, при котором может быть обеспечен AQL на уровень ниже или выше соответственно.
По усмотрению уполномоченной стороны величина fs для усиленного контроля может быть использована для нормального или ослабленного контроля. При этой альтернативной процедуре выбор между s- и s-методам и не связан с правилами переключения.
В.5.3 Кривая приемки
Если даны предельные значения с общим уровнем качества, можно рассчитать ряд значений m и s, дающих значения рU и pL, в сумме равные AQL. Можно нанести эти значения на плоскость в координатах (m, s) и через эти точки провести кривую (рисунок 13). Эта кривая располагается внутри треугольника, соответствующего пределам двустороннего допуска, имеющего свои AQL (рисунок 10). Вблизи U и L эта кривая не отличима от прямой с наклоном минус K и плюс K соответственно, а затем она плавно изгибается, проходя через точку s=MPSD и m=(U+L)/2 (рисунок 13).

Рисунок 13 - Кривая приемки для р=AQL=10 % для предельных значений с общим уровнем качества в координатах (m, s)
На практике значение m неизвестно, и его предстоит оценить на основании выборки; обычно также нужно оценить значение s.
Наилучшую оценку m дает среднее выборки ![]() . В зависимости от обстоятельств s либо принимается известным, либо оценивается по
выборке одним из двух методов. Эти два подхода к определению s приводят к s-методу, s-методу
(и R-методу, приведенному в приложении С) для оценки партии.
. В зависимости от обстоятельств s либо принимается известным, либо оценивается по
выборке одним из двух методов. Эти два подхода к определению s приводят к s-методу, s-методу
(и R-методу, приведенному в приложении С) для оценки партии.
Используя оценки значений m и s, получают оценку параметра качества q. Она известна как статистика качества Q.
Можно рассчитать значение контрольного норматива K, которое для данного объема выборки и метода оценки стандартного отклонения процесса дает гарантию, что с заданной вероятностью партия приемлема, если статистика качества Q больше или равна K.
В.7 s-метод
В.7.1 Получение контрольного норматива
В определенных условиях, то есть когда процесс протекает в течение некоторого времени и с применением статистического контроля качества, s принимают известным и постоянным.
Значения средних последовательных партий не считают постоянными или известными, поэтому каждое значение следует оценить через среднее случайной выборки единиц продукции, взятой от партии.
Среднее выборки ![]() необязательно равно
среднему генеральной совокупности m, но статистика
необязательно равно
среднему генеральной совокупности m, но статистика ![]() распределена нормально
со средним m=0 и стандартным
отклонением, равным 1, так что можно показать, что для данной вероятности
разность среднего выборки и среднего партии не превышает определенного значения
величины.
распределена нормально
со средним m=0 и стандартным
отклонением, равным 1, так что можно показать, что для данной вероятности
разность среднего выборки и среднего партии не превышает определенного значения
величины.
Например, для вероятности 95 % это будет
±1,96![]() .
.
Формулу для верхней статистики качества QU=(U-![]() )/s можно записать в другом виде:
)/s можно записать в другом виде:
![]() .
.
Первый член в правой части - постоянный,
а второй - нормированное отклонение среднего. Поэтому ![]() (как и
(как и ![]() QL) также имеет нормальное распределение со стандартным
отклонением, равным 1. Следовательно, можно так рассчитать k, чтобы для данных объема выборки и AQL статистический показатель качества для выборки был с
заданной вероятностью больше или равен k, если партия приемлема.
QL) также имеет нормальное распределение со стандартным
отклонением, равным 1. Следовательно, можно так рассчитать k, чтобы для данных объема выборки и AQL статистический показатель качества для выборки был с
заданной вероятностью больше или равен k, если партия приемлема.
В.7.2 Критерии приемлемости для одностороннего или двустороннего допуска
Для значения контрольного норматива k, рассчитанного по В.7.1 и приведенного для нормального, усиленного и ослабленного контроля в таблицах IIIA, IIIB и IIIC соответственно, критерий приемлемости для одностороннего допуска приобретает вид:
для верхнего предела поля допуска
партия принимается, если ![]() ;
;
для нижнего предела поля допуска
партия принимается, если ![]()
в других случаях партия не принимается.
Если задан двусторонний допуск, то критерий приемлемости имеет вид:
партия принимается, если kU³ kU и QL³kL;
партия не принимается, если QU<kU или QL>kL.
Так как значение s известно, на практике удобнее преобразовать критерии
приемлемости, придав им следующий вид: ![]() £U-ks - для верхнего предела и
£U-ks - для верхнего предела и ![]() ³L+ks - для нижнего предела, так как правую часть этих
критериев можно определить заранее.
³L+ks - для нижнего предела, так как правую часть этих
критериев можно определить заранее.
В.7.3 Критерии приемлемости для пределов двустороннего допуска с общим AQL
Если даны пределы двустороннего допуска с общим AQL, то для того, чтобы принять решение о приемлемости партии, точку с координатами
![]()
можно нанести на соответствующую диаграмму (см. раздел 4
настоящего стандарта, диаграммы, начиная с s-С до s-Р), в соответствии с В.5.3. Так как s известна, эта точка будет лежать на вертикали,
соответствующей этому значению s. Поэтому на практике достаточно получить ![]() и
и ![]() - приемлемые верхний и нижний пределы приемки
- приемлемые верхний и нижний пределы приемки ![]() (рисунок 14).
(рисунок 14).

Рисунок 14 - Приемочная карта для предельных значений с общим уровнем качества
Критерии приемлемости приобретают вид:
партия принимается, если ![]() £
£![]() и
и ![]() ³
³![]() ;
;
партия не принимается, если ![]() >
>![]() или
или ![]() <
<![]() .
.
В.8 s-метод
В.8.1 Получение контрольного норматива
Когда и среднее, и стандартное отклонение
генеральной совокупности неизвестны, их оценивают по выборке, взятой из этой
совокупности. В s-методе вместо m и s генеральной совокупности берут среднее ![]() и стандартное
отклонение s, полученное из выборки по
формуле
и стандартное
отклонение s, полученное из выборки по
формуле
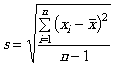 .
.
Таким образом,
![]() или
или ![]() .
.
По сравнению с s-методом это увеличивает вероятность ошибки, так как
установлено, что при подстановке s
вместо s в выражение ![]() (В.7.1) величина
(В.7.1) величина ![]() , которую можно записать в виде
, которую можно записать в виде
![]() ,
,
уже не имеет нормального распределения, а имеет t-распределение с (n-1) степенями свободы. Например, если n=10, то с вероятностью 95 % разность среднего
выборки и среднего партии не превысит значения, равного ±2,26![]() , по сравнению с ±l,96
, по сравнению с ±l,96![]() ,
приведенным в В.7.1.
,
приведенным в В.7.1.
Далее,
![]() ,
,
что можно записать в виде
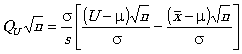 .
.
Далее находим
![]() ,
,
что можно записать в виде
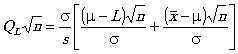 .
.
Эти статистики не являются нормально распределенными, а подчиняются нецентральному t-распределению.
Контрольный норматив k рассчитан с использованием нецентрального t-распределения для стандартного диапазона объемов выборок и AQL и приводится в таблицах IIА, IIВ и IIС для нормального, усиленного и ослабленного контроля соответственно.
В.8.2 Критерии приемлемости для одностороннего и двустороннего допуска
Критерии приемлемости по В.6 подобны приведенным в В.5, но с подстановкой значений оценок среднего, стандартного отклонения и статистики качества, полученных на выборке, и сравнением статистики качества с контрольным нормативом k, рассчитанным для этого метода.
Критерий приемлемости для одностороннего допуска имеет вид:
партия принимается, если QU³k или QL³k;
партия не принимается, если QU<k или QL<k.
Для двустороннего допуска критерий приемлемости имеет вид:
партия принимается, если и QU³kU, и QL³kL;
партия не принимается, если либо QU<kU, либо QL<kL.
Графический метод, показанный на рисунках 8, 9 и 10, также применим к обоим критериям. Пример приведен в 14.3 и показан на рисунке 2 настоящего стандарта.
Верхняя граница зоны приемки по верхнему
пределу поля допуска задается прямой линией ![]() =U-ks, нижняя граница по нижнему пределу - прямой линией
=U-ks, нижняя граница по нижнему пределу - прямой линией ![]() =L+ks. Если заданы верхний и нижний пределы поля допуска,
зоной приемки является область между этими двумя линиями и осью
=L+ks. Если заданы верхний и нижний пределы поля допуска,
зоной приемки является область между этими двумя линиями и осью ![]() , как показано на рисунке
2 настоящего стандарта.
, как показано на рисунке
2 настоящего стандарта.
В.8.3 Критерии приемлемости для двустороннего допуска с общим AQL
В разделе В.5.3 показано, что если заданы пределы поля допуска с общим AQL, приемлемость процесса зависит от того, располагается ли точка (s, m) внутри соответствующей кривой приемки на диаграмме приемки (см. рисунок 13).
Определить приемлемость партии можно,
нанеся полученные на основе выборки значения s и ![]() на подобную диаграмму
приемки с соответствующими объемом выборки и AQL.
на подобную диаграмму
приемки с соответствующими объемом выборки и AQL.
Кривые приемки для стандартных планов,
приведенных в настоящем стандарте, рассчитаны с учетом неопределенности, вносимой
при использовании оценок ![]() и s для m и s соответственно в s-методе.
и s для m и s соответственно в s-методе.
Эти кривые приведены в разделе 4 на
диаграммах, начиная с s-D no s-P.
Они приведены к единому масштабу, то есть вместо координат ![]() и s при
использовании s-метода применяются координаты
и s при
использовании s-метода применяются координаты
![]() ,
,
Область приемки для кодов В и С (то есть
для объемов выборки 3 и 4) ограничена четырьмя прямыми - осью ![]() ; прямой
; прямой ![]() =U-ks; прямой, параллельной оси
=U-ks; прямой, параллельной оси ![]() , проходящей через MSSD, (таблица IVs), и прямой
, проходящей через MSSD, (таблица IVs), и прямой ![]() =L+ks, где значение k определяют по таблицам IIА, IIВ или IIС.
=L+ks, где значение k определяют по таблицам IIА, IIВ или IIС.
Критерий приемлемости имеет вид:
партия принимается, если точка [s/(U-L); (![]() -L)/(U-L)] лежит
внутри зоны приемки;
-L)/(U-L)] лежит
внутри зоны приемки;
партия не принимается, если точка лежит вне этой зоны.
На практике при контроле серии партий
задача контролера облегчается, если для установленного плана выборочного
контроля создается специальная кривая приемки в координатах s и ![]() (рисунок 3), как
для нормального, так и для усиленного контроля.
(рисунок 3), как
для нормального, так и для усиленного контроля.
Если s больше MSSD (полученное по таблице IV), партия должна быть отклонена (сравни с В.5.2).
В.8.4 Комбинированные пределы поля допуска
Если задаются комбинации указанных выше типов пределов поля допуска, например AQL (соответствующий контрольному нормативу k1) для верхнего предела в сочетании с общим AQL, то на приемочной карте строятся предельные линии или кривые, а зоной приемки является область, общая для обоих условий (рисунок 15).

Рисунок 15 - Карта приемки для комбинированных пределов поля допуска (s-метод)
ПРИЛОЖЕНИЕ С
(обязательное)
Планы выборочного контроля. R-метод
С.1 Цель
Этот метод создает альтернативу s-методу, приведенному в разделе 14 настоящего стандарта
С.2 Определения
При применении этого метода используются следующие дополнительные термины:
С.2.1 R-метод: Метод определения приемлемости партии через оценку стандартного отклонения, основанную на среднем размахе измерений показателя качества в подгруппах выборки.
С.2.2 подгруппа: Пять единиц продукции, взятых в том порядке, в котором они подвергались измерению.
С.2.3 размах (R): При использовании R-метода смысл этого понятия ограничен, а именно: размах для подгруппы.
Примечание - В своем обычном значении размах - это разность между наибольшим и наименьшим наблюдаемыми значениями величин.
С.2.4 средний размах (![]() ): Среднее значение размахов в подгруппах. Для выборок
менее чем из десяти единиц за
): Среднее значение размахов в подгруппах. Для выборок
менее чем из десяти единиц за ![]() принимают размах для всей
выборки.
принимают размах для всей
выборки.
С.2.5 максимальный средний размах (MAR): Наибольший, приемлемый в данных условиях, средний размах.
С.3 Обозначения
Для этого метода используются следующие дополнительные обозначения:
с - коэффициент масштаба для определения s по ![]() , приведенный в таблице RI
настоящего приложения;
, приведенный в таблице RI
настоящего приложения;
F- коэффициент, приведенный в таблице RI и представляющий собой отношение максимального среднего размаха к разности U и L;
k - контрольный норматив;
R - размах для подгруппы;
![]() - средний размах на основе данных по
нескольким подгруппам.
- средний размах на основе данных по
нескольким подгруппам.
R-метод обеспечивает альтернативный способ оценки стандартного отклонения.
Для выборок малого объема величины R и s,
рассчитанные для одной и той же нормальной выборки, сильно коррелированы, что
позволяет использовать R в качестве
оценки для s. Эту взаимосвязь используют,
когда работают с выборками, в которых меньше чем по десять изделий. С
увеличением объема выборки величина R становится менее точной оценкой и ее не следует
использовать в качестве оценки s. Но
если эту выборку произвольно разбить на небольшие подгруппы одинакового объема,
то средний для них размах ![]() можно использовать
для оценки стандартного отклонения партии.
можно использовать
для оценки стандартного отклонения партии.
В стандартных планах для R-метода объемы выборок кратны пяти, за исключением
трех планов, в которых объем выборок составляет 3, 4 и 7. Выборку разбивают на
подгруппы по пять изделий, определяют размах R в каждой подгруппе и получают таким образом средний
размах ![]() . Если в выборке менее 10 изделий, ее не разбивают на
подгруппы, а размах используют, как если бы это был средний размах.
. Если в выборке менее 10 изделий, ее не разбивают на
подгруппы, а размах используют, как если бы это был средний размах.
Коэффициент масштаба рассчитывают, исходя
из объема подгруппы и количества подгрупп, так что s можно заменить выражением ![]() /с. В таблице RI
приведен коэффициент масштаба с для различных объемов выборок на основе
используемых в настоящем стандарте объемов подгрупп.
/с. В таблице RI
приведен коэффициент масштаба с для различных объемов выборок на основе
используемых в настоящем стандарте объемов подгрупп.
Однако нет необходимости в использовании коэффициента масштаба с, приведенного в таблице RI, так как для упрощения вычислений для R-метода создан специальный набор таблиц. В этом случае верхняя и нижняя статистики качества определяются непосредственно из формул:
![]() и
и ![]() ,
,
В таблице RI дается также сравнение кодов объема выборок для R-метода, s-метода и контроля по альтернативному признаку по ГОСТ Р 50779.71. Объем выборки для R-метода несколько больше, чем для s-метода, и в обоих случаях меньше, чем для метода контроля по альтернативному признаку.
Контрольный норматив k для каждого плана контроля вычисляют так, что критерии приемлемости для верхнего предела одностороннего допуска имеют вид:
партия принимается, если ![]() ³k,
³k,
для нижнего предела одностороннего допуска:
партия принимается, если ![]() ³k,
³k,
в других случаях партия не принимается.
Если задан двусторонний допуск, критерии приемлемости таковы:
партия принимается, если и QU³kU и QL³kL;
партия не принимается, если либо QU<kU, либо QL<kL.
Подставив ![]() вместо s, можно применить графический метод по 14.3 настоящего
стандарта. Если задан двусторонний допуск с общим AQL, точку
вместо s, можно применить графический метод по 14.3 настоящего
стандарта. Если задан двусторонний допуск с общим AQL, точку
![]()
наносят на соответствующую диаграмму (R-D - R-P), чтобы
установить, приемлема ли партия. Следует обратить внимание, что в R-методе эквивалентом максимального выборочного
стандартного отклонения MSSD является
максимальный средний размах MAR. Его
значение можно найти в таблице RIV
по объему выборки и AQL. Точка [![]() =MAR;
=MAR; ![]() =1/2(U+L)] образует пик кривой приемки. Если значение величины
=1/2(U+L)] образует пик кривой приемки. Если значение величины
![]() больше MAR, партия не принимается.
больше MAR, партия не принимается.
С.6 Оперативная характеристика
Оперативные характеристики, рассчитанные для s-метода, применимы и к R-методу, но дают несколько меньшую точность. Выбирают их по коду объема выборки и значению AQL.
С.7 Контрольные карты
Регистрация данных в форме контрольных карт, рекомендованная в 18.1 настоящего стандарта, в равной степени применима и к R-методу.
Если задан двусторонний_допуск с общим AQL, на R-карту следует наносить MAR.
Если оказывается, что ![]() стабилен, то корень
из средневзвешенных значений квадратов значений величин
стабилен, то корень
из средневзвешенных значений квадратов значений величин ![]() /c можно
предположить равным s, и тогда множитель с берут из таблицы RI. В этом случае, а также если получено разрешение на
переход к этому методу от уполномоченной стороны, применим s-метод (А.2, приложение А).
/c можно
предположить равным s, и тогда множитель с берут из таблицы RI. В этом случае, а также если получено разрешение на
переход к этому методу от уполномоченной стороны, применим s-метод (А.2, приложение А).
С.8 Выбор метода
Если имеется калькулятор, рекомендуется использовать s-метод, но если расчет s для этого метода создает трудности, то в качестве альтернативы этому методу можно использовать R-метод.
R-метод прост для расчета, но требует некоторого увеличения объема выборки.
С.9 Работа с планом выборочного контроля по R-методу
С.9.1 Получение плана контроля
Проверьте сначала, что приведенные в разделе 13 настоящего стандарта рекомендации выполнены.
Стандартная процедура для выбора плана по R-методу такова:
a) исходя из заданных уровня контроля (как правило, уровень контроля II) и объема партии, необходимо определить по таблице IA код объема выборки;
b) используя заданный AQL, необходимо определить по таблице RIIA настоящего приложения объем выборки п и контрольный норматив k.
С.9.2 Работа с планом контроля
С.9.2.1 Отберите в случайном порядке отдельные единицы выборки и измерьте в них контролируемый параметр. Результаты измерений запишите в том же порядке.
С.9.2.2 Найдите сумму Sx всех измеренных значений и, поделив ее на n - количество изделий в выборке, получите выборочное среднее
![]()
С.9.2.3 Получение значения величины ![]() :
:
a) если изделий 10 или более, разбейте
данные в порядке выполнения измерений на подгруппы по 5 (это всегда возможно,
так как по стандартным планам количество изделий в выборках большого объема
кратно пяти). Путем вычитания наименьшего измерения из наибольшего, получите
размах измерений в каждой подгруппе, а затем подсчитайте средний размах ![]() ;
;
b) выборки менее чем из 10 изделий на
подгруппы не делят, разность наибольшего и наименьшего значений дает размах,
который затем используют как средний размах ![]() .
.
С.9.2.4 Применение критерия приемки
Если заданы односторонний или двусторонний допуски, рассчитайте статистику качества Q по формулам:
QU=(U-![]() )/
)/![]()
и(или)
QL=(![]() -L)/
-L)/ ![]() .
.
Сравните статистику качества [QU и(или) QL] с контрольным нормативом [kU и(или) kL], взятого из таблицы RIIA для нормального контроля. Если статистика качества больше или равна значению k, партия принимается, если меньше - нет. Таким образом, если задан только верхний предел поля допуска U, то
партия принимается, если QU³k;
партия не принимается, если QU<k.
Если задан только нижний предел поля допуска L, то
партия принимается, если QL³ k;
партия не принимается, если QL<k.
Если заданы и U и L (значения k различны, АQL для пределов двустороннего допуска различны), то
партия принимается, если и QL³kL, и QU³kU;
партия не принимается, если QL<kL или QU<kU.
Пример - Нижний предел поля допуска для электрического сопротивления некоторого элемента равен 580 Ом. Контролю подвергается партия из 100 изделий. Уровень контроля II, нормальный контроль с AQL=1 %. По таблице IA находим код F. Таблица RIIA показывает, что требуемый объем выборки - 10, а контрольный норматив равен 0,073. Допустим, что значения сопротивления, полученные в выборке, располагаются в следующем порядке:
первая подгруппа 610; 615; 629; 593; 617 дает R=629-593=36;
вторая подгруппа 623; 589; 608; 591; 611 дает R=623-589=34.
Необходимо определить соответствие критерию приемки.
|
Необходимая информация |
Полученные значения |
|
Объем выборки: n |
10 |
|
Выборочное
среднее |
608,6 |
|
Средний
размах |
35 |
|
Нижнее предельное значение: L |
580 |
|
QL=( |
0,817 |
|
Контрольный норматив: k (таблица RIIA) |
0,703 |
|
Критерий приемки: сравниваем QL с k |
0,817>0,703 |
Партия соответствует критерию приемки, так как QL больше k.
С.9.2.5 Если требуется построить критерий приемки на графике,
то для одностороннего или двустороннего допуска надо провести прямую,
представленную уравнением ![]() =U-k
=U-k![]() (для верхнего
предела), которая проводит через точку (
(для верхнего
предела), которая проводит через точку (![]() =0;
=0; ![]() =L) с
наклоном минус k, и (или) прямую,
представленную уравнением
=L) с
наклоном минус k, и (или) прямую,
представленную уравнением ![]() =L+k
=L+k![]() (для нижнего
предела), которая проходит через точку (
(для нижнего
предела), которая проходит через точку (![]() =0;
=0; ![]() =L) c наклоном плюс k, на миллиметровой бумаге, откладывая значения
=L) c наклоном плюс k, на миллиметровой бумаге, откладывая значения ![]() по вертикальной оси и
по вертикальной оси и
![]() - по горизонтальной.
Этот график можно построить перед тем, как приступить к контролю серии партий
(в соответствии с процедурой, приведенной в 14.3 для s-метода). Затем необходимо взять значения
- по горизонтальной.
Этот график можно построить перед тем, как приступить к контролю серии партий
(в соответствии с процедурой, приведенной в 14.3 для s-метода). Затем необходимо взять значения ![]() и
и ![]() полученные на основе
результатов измерений в каждой выборке, и нанести точку (
полученные на основе
результатов измерений в каждой выборке, и нанести точку (![]() ,
,![]() ). Если эта точка попадает в зону приемки, партия
принимается, если нет - не принимается.
). Если эта точка попадает в зону приемки, партия
принимается, если нет - не принимается.
Пример - Используя данные, приведенные в предыдущем примере,
отметим на оси ![]() точку L=580 и проведем через эту точку линию с наклоном k=0,703. Эта линия проходит через точки (
точку L=580 и проведем через эту точку линию с наклоном k=0,703. Эта линия проходит через точки (![]() =10;
=10; ![]() =587), (
=587), (![]() =20;
=20; ![]() =594,1), (
=594,1), (![]() =40;
=40; ![]() =608,1) и т.д. Выбираем соответствующую точку и проводим
прямую через нее и через (
=608,1) и т.д. Выбираем соответствующую точку и проводим
прямую через нее и через (![]() =0;
=0; ![]() =580), то есть через L. Область над этой прямой образует зону приемки.
Подсчитано, что
=580), то есть через L. Область над этой прямой образует зону приемки.
Подсчитано, что ![]() и
и ![]() равны 35 и 608,6
соответственно. Отметим точку (
равны 35 и 608,6
соответственно. Отметим точку (![]() =35;
=35; ![]() =608,6) на графике. Из рисунка
16 видим, что она располагается в зоне приемки и что партию можно принять.
=608,6) на графике. Из рисунка
16 видим, что она располагается в зоне приемки и что партию можно принять.
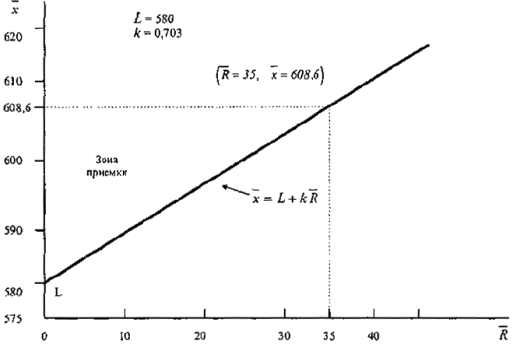
Рисунок 16 - Графический метод для одностороннего допуска и предельных значений с общим уровнем качества
Если заданы предельные значения с общим
уровнем качества, необходимо пользоваться графическим методом, если только ![]() не больше, чем MAR по таблице RIV.
В последнем случае партию можно сразу отклонить.
не больше, чем MAR по таблице RIV.
В последнем случае партию можно сразу отклонить.
По коду объема выборки выберем соответствующую диаграмму для R-метода. На этой диаграмме выберем кривую приемки, соответствующую заданному AQL.
Скопируем на кальку эту кривую и ближайшую к ней кривую внутри ее (внутренняя кривая необходима, если потребуется переключиться на усиленный контроль), тогда область между этими двумя кривыми образует зону предупреждения.
Вычислим значения
![]()
и нанесем их на кальку с этими кривыми.
Если эта точка располагается вне зоны приемки, партия не принимается, в других случаях - принимается.
Примечание - Рабочую кривую удобнее было бы привести в
такой шкале, чтобы можно было непосредственно наносить ![]() и
и ![]() (рисунок 17).
(рисунок 17).
Пример - Допуск на сопротивление некоторого электроэлемента составляет (520±50) Ом. Контролю подвергается партия из 350 изделий. Используется уровень контроля II, нормальный контроль, AQL=4 %. По таблице IA находим код F. Таблица RIIA показывает, что требуемый объем выборки - 25, а таблица RIV - что для MAR значение F равно 0,707. Предположим, что значения сопротивления в выборке получены в следующем порядке:
Первая подгруппа- 515; 491; 479; 507; 543;
(R=543-479=64).
Вторая подгруппа -521; 536; 483; 509; 514;
(R=536-483=53).
Третья подгруппа - 507; 484; 526; 552; 499;
(R =552-484=68).
Четвертая подгруппа - 530; 512; 492; 521; 467;
(R=530-467=63).
Пятая подгруппа - 489; 513; 535; 501; 529;
(R=535-489=46).
|
Необходимая информация |
Полученные значения |
|
Объем выборки: n |
25 |
|
Выборочное
среднее |
510,2 |
|
Средний
размах |
58,8 |
|
Верхний предел допуска: U |
570 |
|
Нижний предел допуска: L |
470 |
|
Нормированное
среднее: ( |
0,402 |
|
Нормированный
средний размах: |
0,583 |
|
Значение F (таблица RIV) |
0,707 |
|
MAR=F(U-L) |
70,7 |
Нормированные значения среднего выборки и среднего размаха наносят затем на график R-H, AQL=4 % (рисунок 17). Если нанесенная точка располагается вне кривой приемки, партия отклоняется.
Точка (0,588; 0,402) лежит внутри кривой приемки, значит партия принимается.
С.10 Процедура непрерывного контроля
При использовании R-метода применяется процедура, приведенная в разделах 16-22 настоящего стандарта для s-метода.

Рисунок 17 - Кривая приемки для кода Н, п=25, AQL=4 %, MAR=70,7: (R-метод)
Таблица RI - Коды, объемы выборок и коэффициент масштаба: R-метод
|
R-метод |
|
Эквивалентный объем выборки |
||||
|
Код |
Объем выборки |
Число подгрупп |
с |
s-метод |
ГОСТ Р 50779.71 |
|
|
В |
3 |
- |
1,910 |
3 |
3 |
|
|
С |
4 |
- |
2,234 |
4 |
5 |
|
|
D |
5 |
- |
2,474 |
5 |
8 |
|
|
Е |
7 |
- |
2,830 |
7 |
13 |
|
|
F |
10 |
2 |
2,405 |
10 |
20 |
|
|
G |
15 |
3 |
2,379 |
15 |
32 |
|
|
Н |
25 |
5 |
2,358 |
20 |
50 |
|
|
I |
30 |
6 |
2,353 |
25 |
- |
|
|
J |
40 |
8 |
2,346 |
35 |
80 |
|
|
К |
60 |
12 |
2,339 |
50 |
125 |
|
|
L |
85 |
17 |
2,335 |
75 |
200 |
|
|
М |
115 |
23 |
2,333 |
100 |
315 |
|
|
N |
175 |
35 |
2,331 |
150 |
500 |
|
|
Р |
230 |
46 |
2,330 |
200 |
800 |
|
|
Примечания 1 Определение с - по С.4. 2 Коды в настоящем стандарте соответствуют кодам, приведенным в ГОСТ Р 50779.71. |
|
|||||
Таблица RIIA - Одноступенчатые выборочные планы для нормального контроля (основная таблица): R-метод
|
Код объема выборки |
Объем выборки |
Приемлемые уровни качества AQL (нормальный контроль) |
||||||||||
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,00 |
1,50 |
2,50 |
4,00 |
6,50 |
10,00 |
||
|
k |
k |
k |
k |
k |
k |
k |
k |
k |
k |
k |
||
|
В |
3 |
|
|
|
|
|
|
|
0,587 |
0,502 |
0,401 |
0,269 |
|
С |
4 |
0,651 |
0,598 |
0,525 |
0,450 |
0,364 |
0,276 |
|||||
|
D |
5 |
0,663 |
0,614 |
0,565 |
0,498 |
0,431 |
0,352 |
0,272 |
||||
|
Е |
7 |
0,702 |
0,659 |
0,613 |
0,569 |
0,525 |
0,465 |
0,405 |
0,336 |
0,266 |
||
|
F |
10 |
0,916 |
0,863 |
0,811 |
0,775 |
0,703 |
0,650 |
0,579 |
0,507 |
0,424 |
0,341 |
|
|
G |
15 |
0,999 |
0,958 |
0,903 |
0,850 |
0,792 |
0,738 |
0,684 |
0,610 |
0,536 |
0,452 |
0,368 |
|
Н |
25 |
1,05 |
1,01 |
0,951 |
0,896 |
0,835 |
0,779 |
0,723 |
0,647 |
0,571 |
0,484 |
0,398 |
|
I |
30 |
1,06 |
1,02 |
0,959 |
0,904 |
0,843 |
0,787 |
0,730 |
0,654 |
0,577 |
0,490 |
0,403 |
|
J |
40 |
1,08 |
1,04 |
0,978 |
0,921 |
0,860 |
0,803 |
0,746 |
0,668 |
0,591 |
0,503 |
0,415 |
|
К |
60 |
1,11 |
1,06 |
1,00 |
0,948 |
0,885 |
0,826 |
0,768 |
0,689 |
0,610 |
0,521 |
0,432 |
|
L |
85 |
1,13 |
1,08 |
1,02 |
0,962 |
0,899 |
0,839 |
0,780 |
0,791 |
0,621 |
0,530 |
0,441 |
|
М |
115 |
1,14 |
1,09 |
1,03 |
0,975 |
0,911 |
0,851 |
0,791 |
0,711 |
0,631 |
0,539 |
0,449 |
|
N |
175 |
1,16 |
1,11 |
1,05 |
0,994 |
0,929 |
0,868 |
0,807 |
0,726 |
0,644 |
0,552 |
0,460 |
|
Р |
230 |
1,16 |
1,12 |
1,06 |
0,996 |
0,931 |
0,870 |
0,809 |
0,728 |
0,646 |
0,563 |
0,462 |
|
Примечания к таблицам RIIA-RIIC: 1 Все значения AQL выражены в процентах несоответствующих единиц продукции. 2 Коды объема выборки в настоящем стандарте соответствуют приведенным в ГОСТ Р 50779.71. 3 Символы указывают:
|
||||||||||||
Таблица RIIB - Одноступенчатые выборочные планы для усиленного контроля (основная таблица): R-метод
|
Код объема выборки |
Объем выборки |
Приемлемые уровни качества AQL (усиленный контроль) |
||||||||||
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,00 |
1,50 |
2,50 |
4,00 |
6,50 |
10,00 |
||
|
k |
k |
k |
k |
k |
k |
k |
k |
k |
k |
k |
||
|
В |
3 |
|
|
|
|
|
|
|
|
0,587 |
0,502 |
0,401 |
|
С |
4 |
0,651 |
0,598 |
0,525 |
0,450 |
0,364 |
||||||
|
D |
5 |
0,663 |
0,614 |
0,565 |
0,498 |
0,431 |
0,352 |
|||||
|
Е |
7 |
0,702 |
0,659 |
0,613 |
0,569 |
0,525 |
0,465 |
0,405 |
0,336 |
|||
|
F |
10 |
0,916 |
0,863 |
0,811 |
0,755 |
0,703 |
0,650 |
0,579 |
0,507 |
0,424 |
||
|
G |
15 |
1,04 |
0,999 |
0,958 |
0,903 |
0,850 |
0,792 |
0,738 |
0,684 |
0,610 |
0,536 |
0,452 |
|
Н |
25 |
1,10 |
1,05 |
1,01 |
0,951 |
0,896 |
0,835 |
0,779 |
0,723 |
0,647 |
0,571 |
0,484 |
|
I |
30 |
1,10 |
1,06 |
1,02 |
0,959 |
0,904 |
0,843 |
0,787 |
0,730 |
0,654 |
0,577 |
0,490 |
|
J |
-40 |
1,13 |
1,08 |
1,04 |
0,978 |
0,921 |
0,860 |
0,803 |
0,746 |
0,668 |
0,591 |
0,503 |
|
К |
60 |
1,16 |
1,11 |
1,06 |
1,00 |
0,948 |
0,885 |
0,826 |
0,768 |
0,689 |
0,610 |
0,521 |
|
L |
85 |
1,17 |
1,13 |
1,08 |
1,02 |
0,962 |
0,899 |
0,839 |
0,780 |
0,701 |
0,621 |
0,530 |
|
М |
115 |
1,19 |
1,14 |
1,09 |
1,03 |
0,975 |
0,911 |
0,851 |
0,791 |
0,711 |
0,631 |
0,539 |
|
N |
175 |
1,21 |
1,16 |
1,11 |
1,05 |
0,994 |
0,929 |
0,868 |
0,807 |
0,726 |
0,644 |
0,552 |
|
Р |
230 |
1,21 |
1,16 |
1,12 |
1,06 |
0,996 |
0,931 |
0,870 |
0,8091 |
0,728 |
0,646 |
0,553 |
Таблица RIIC - Одноступенчатые выборочные планы для ослабленного контроля (основная таблица): R-метод
|
Код объема выборки |
Объем выборки |
Приемлемые уровни качества AQL (ослабленный контроль) |
||||||||||||
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,00 |
1,50 |
2,50 |
4,00 |
6,50 |
10,00 |
||||
|
k |
k |
k |
k |
k |
k |
k |
k |
k |
k |
k |
||||
|
В |
3 |
|
|
|
|
|
|
|
|
0,587 |
0,502 |
0,401 |
0,296 |
0,178 |
|
С |
3 |
0,587 |
0,502 |
0,401 |
0,296 |
0,178 |
||||||||
|
D |
3 |
0,587 |
0,502 |
0,401 |
0,296 |
0,178 |
||||||||
|
Е |
3 |
|
|
0,587 |
0,502 |
0,401 |
0,296 |
0,178 |
||||||
|
F |
4 |
0,651 |
0,598 |
0,525 |
0,450 |
0,364 |
0,276 |
0,176 |
||||||
|
G |
5 |
0,663 |
0,614 |
0,565 |
0,498 |
0,431 |
0,352 |
0,272 |
0,184 |
|||||
|
Н |
7 |
0,702 |
0,659 |
0,613 |
0,569 |
0,525 |
0,465 |
0,405 |
0,336 |
0,266 |
0,189 |
|||
|
I |
10 |
0,916 |
0,863 |
0,811 |
0,755 |
0,703 |
0,650 |
0,579 |
0,507 |
0,424 |
0,341 |
0,252 |
||
|
J |
15 |
0,958 |
0,903 |
0,850 |
0,792 |
0,738 |
0,684 |
0,610 |
0,536 |
0,452 |
0,368 |
0,276 |
||
|
К |
25 |
1,01 |
0,951 |
0,896 |
0,835 |
0,779 |
0,723 |
0,647 |
0,571 |
0,484 |
0,398 |
0,305 |
||
|
L |
30 |
1,02 |
0,959 |
0,904 |
0,843 |
0,787 |
0,730 |
0,654 |
0,577 |
0,490 |
0,403 |
0,310 |
||
|
М |
40 |
1,04 |
0,978 |
0,921 |
0,860 |
0,803 |
0,746 |
0,668 |
0,591 |
0,503 |
0,415 |
0,321 |
||
|
N |
60 |
1,06 |
1,00 |
0,948 |
0,885 |
0,826 |
0,768 |
0,689 |
0,610- |
0,521 |
0,432 |
0,336 |
||
|
Р |
85 |
1,08 |
1,02 |
0,962 |
0,899 |
0,839 |
0,780 |
0,701 |
0,621 |
0,530 |
0,441 |
0,345 |
||
Таблица RIV - Значения F для максимального среднего размаха (MAR): R-метод
|
Объем выборки |
Приемлемые уровни качества (нормальный контроль) |
||||||||||||
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,00 |
1,50 |
2,50 |
4,00 |
6,50 |
10,00 |
|
|
|
3 |
|
|
|
|
|
|
|
|
0,833 |
0,865 |
0,907 |
0,958 |
1,028 |
|
4 |
|
|
|
|
|
|
0,756 |
0,788 |
0,836 |
0,891 |
0,965 |
1,056 |
1,180 |
|
5 |
|
|
|
|
|
0,730 |
0,764 |
0,801 |
0,857 |
0,923 |
1,011 |
1,018 |
1,263 |
|
7 |
|
|
|
0,695 |
0,727 |
0,765 |
0,804 |
0,846 |
0,910 |
0,985 |
1,086 |
1,209 |
1,374 |
|
10 |
|
|
0,529 |
0,553 |
0,579 |
0,610 |
0,642 |
0,677 |
0,730 |
0,793 |
0,876 |
0,977 |
1,112 |
|
15 |
0,460 |
0,477 |
0,493 |
0,517 |
0,542 |
0,572 |
0,602 |
0,637 |
0,688 |
0,748 |
0,830 |
0,928 |
1,058 |
|
20 |
0,432 |
0,447 |
0,463 |
0,486 |
0,509 |
0,537 |
0,567 |
0,600 |
0,649 |
0,707 |
0,785 |
0,879 |
1,004 |
|
30 |
0,426 |
0,442 |
0,457 |
0,480 |
0,503 |
0,531 |
0,560 |
0,593 |
0,642 |
0,699 |
0,776 |
0,870 |
0,993 |
|
40 |
0,417 |
0,432 |
0,447 |
0,469 |
0,492 |
0,519 |
0,548 |
0,580 |
0,628 |
0,684 |
0,761 |
0,852 |
0,968 |
|
60 |
0,403 |
0,419 |
0,434 |
0,455 |
0,478 |
0,505 |
0,533 |
0,564 |
0,608 |
0,666 |
0,740 |
0,830 |
0,949 |
|
85 |
0,398 |
0,412 |
0,427 |
0,448 |
0,470 |
0,497 |
0,525 |
0,555 |
0,602 |
0,656 |
0,729 |
0,818 |
0,934 |
|
115 |
0,392 |
0,406 |
0,421 |
0,442 |
0,464 |
0,490 |
0,517 |
0,548 |
0,594 |
0,648 |
0,720 |
0,808 |
0,923 |
|
175 |
0,384 |
0,399 |
0,413 |
0,434 |
0,455 |
0,481 |
0,508 |
0,538 |
0,584 |
0,637 |
0,708 |
0,794 |
0,908 |
|
230 |
0,384 |
0,397 |
0,412 |
0,432 |
0,454 |
0,480 |
0,507 |
0,536 |
0,582 |
0,633 |
0,706 |
0,792 |
0,906 |
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,00 |
1,50 |
2,50 |
4,00 |
6,50 |
10,00 |
|
|
|
Приемлемые уровни качества (усиленный контроль) |
|||||||||||||
|
|
0,10 |
0,15 |
0,25 |
0,40 |
0,65 |
1,00 |
1,50 |
2,50 |
4,00 |
6,50 |
10,00 |
||
|
Приемлемые уровни качества (ослабленный контроль) |
|||||||||||||
|
Примечание - MAR получают путем умножения коэффициента F на разность между верхним U и нижним L пределами поля допуска, то есть MAR=F(U-L). MAR указывает наибольшее допустимое значение среднего размаха выборки при использовании R-метода для двустороннего допуска при неизвестной дисперсии. Если средний размах выборки меньше, чем MAR, нет гарантии, что партия будет принята. |
|||||||||||||
Диаграмма R-D - Кривые приемки для предельных значений с общим уровнем качества: R-метод для кода объема выборки D (объем выборки - 5)
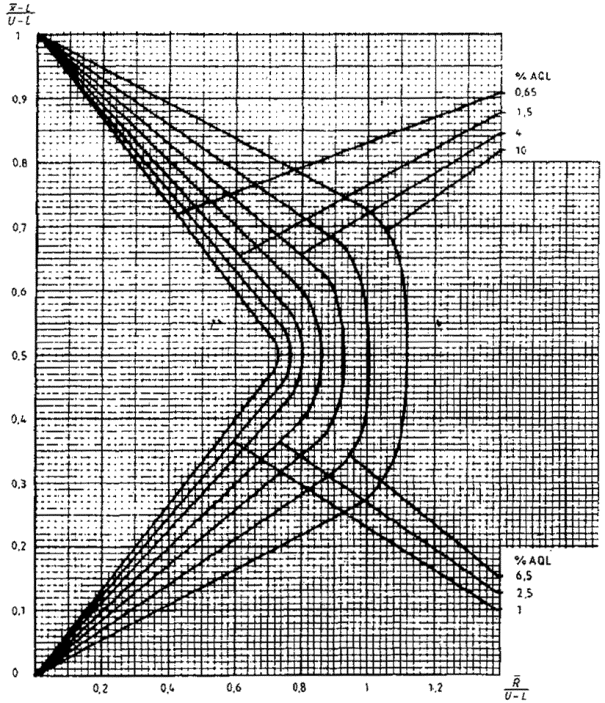
Диаграмма R-E - Кривые приемки для предельных значений с общим уровнем качества: R-метод для кода объема выборки Е (объем выборки - 7)
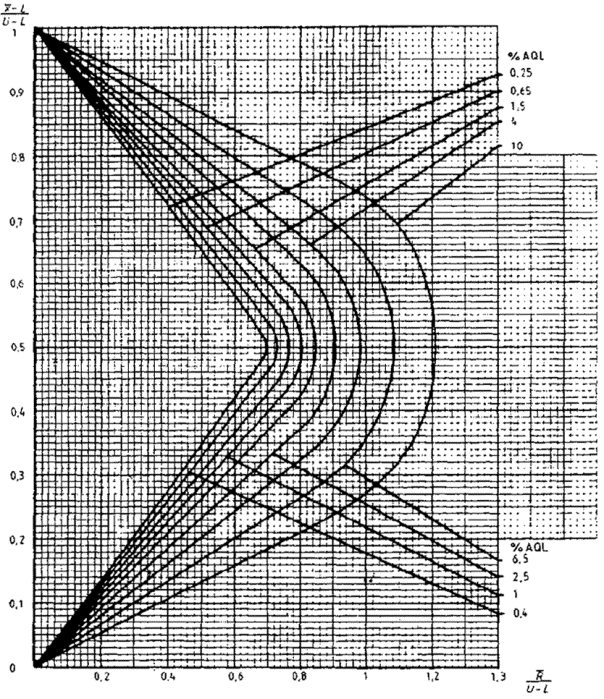
Диаграмма R-F - Кривые приемки для предельных значений с общим уровнем качества: R-метод для кода объема выборки F (объем выборки - 10)
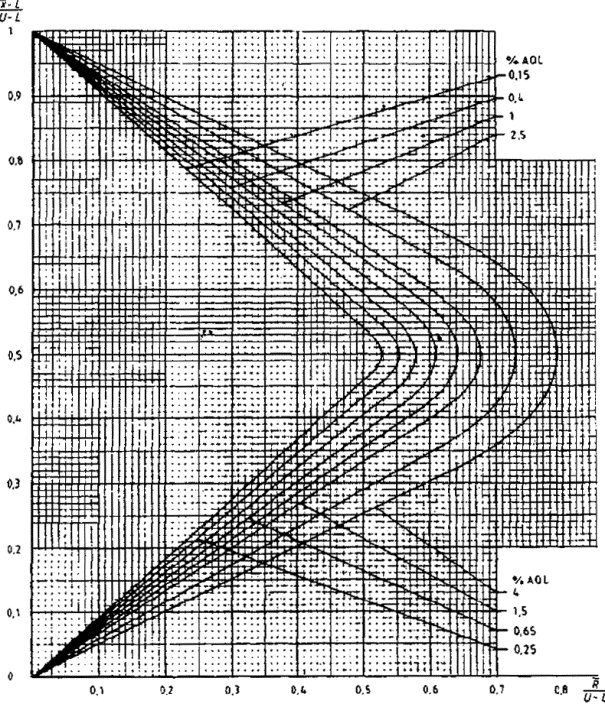
Диаграмма R-G - Кривые приемки для предельных значений с общим уровнем качества: R-метод для кода объема выборки G (объем выборки - 15)

Диаграмма R-H - Кривые приемки для предельных значений с общим уровнем качества: R-метод для кода объема выборки Н (объем выборки - 20)
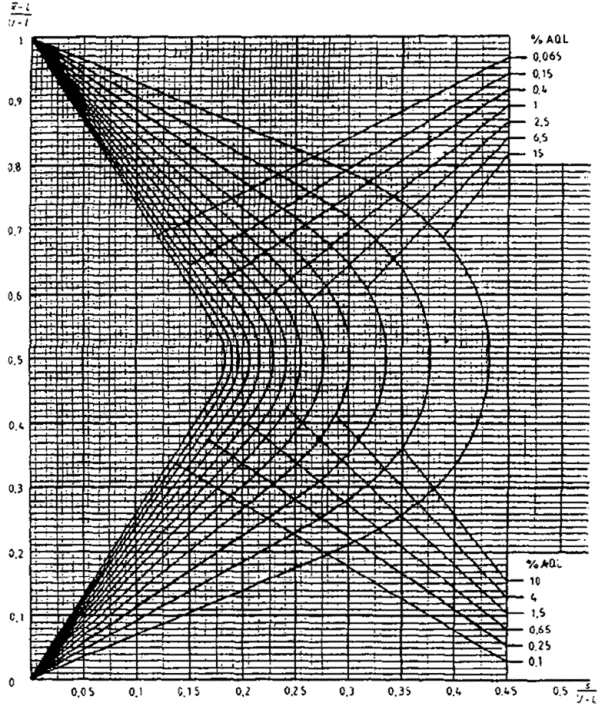
Диаграмма R-I - Кривые приемки для предельных значений с общим уровнем качества: R-метод для кода объема выборки I (объем выборки - 25)

Диаграмма R-J - Кривые приемки для предельных значений с общим уровнем качества: R-метод для кода объема выборки J (объем выборки - 40)

Диаграмма R-K - Кривые приемки для предельных значений с общим уровнем качества: R-метод для кода объема выборки К (объем выборки - 60)

Диаграмма R-L - Кривые приемки для предельных значений с общим уровнем качества: R-метод для кода объема выборки L (объем выборки - 85)
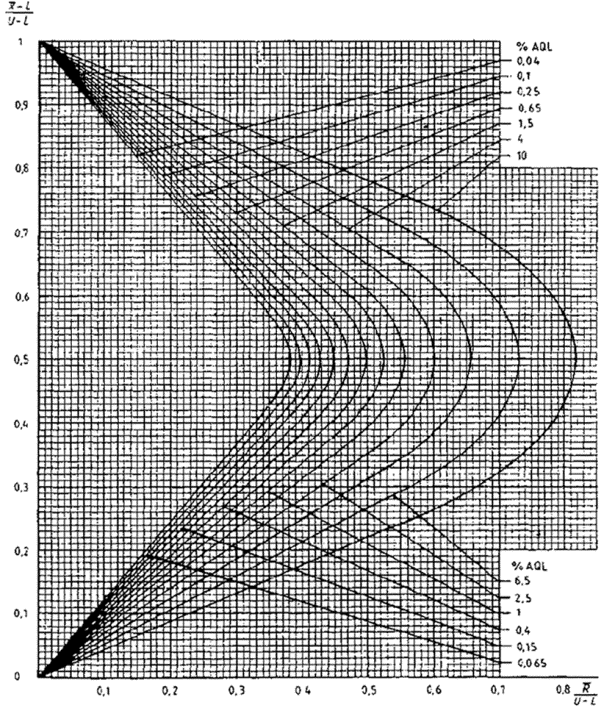
Диаграмма R-M - Кривые приемки для предельных значений с общим уровнем качества: R-метод для кода объема выборки М (объем выборки - 115)
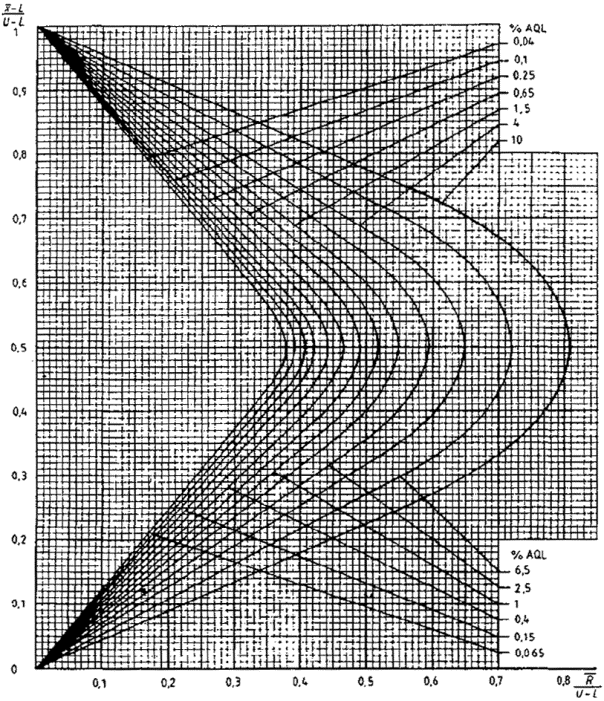
Диаграмма R-N - Кривые приемки для предельных значений с общим уровнем качества: R-метод для кода объема выборки N (объем выборки - 175)
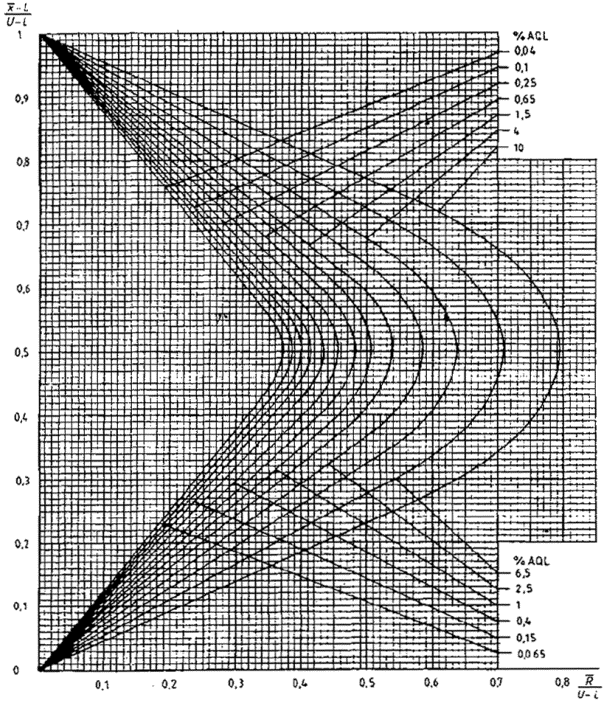
Диаграмма R-P - Кривые приемки для предельных значений с общим уровнем качества: R-метод для кода объема выборки Р (объем выборки - 230)
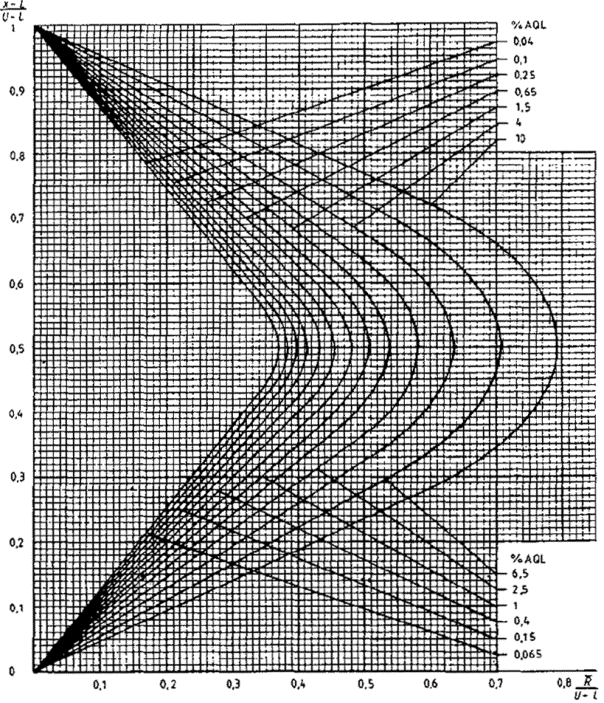
ПРИЛОЖЕНИЕ D
(обязательное)
Графическая бумага для s-метода
Для того, чтобы приспособить систему кривых приемки s-метода для двустороннего допуска с общим AQL без изменения масштаба, производится специальная форма графической бумаги с уменьшенным масштабом (сжатым по горизонтали). Лист этой бумаги показан на рисунке 18.
Если применяют выборочные планы s-метода для двустороннего допуска с общим AQL, соответствующие кривые приемки можно скопировать (или перенести на кальку) на фотокопию рисунка 18 (по 14.6).

Рисунок 18 - Графическая бумага для s-метода
ПРИЛОЖЕНИЕ Е
(обязательное)
Взаимосвязь настоящего стандарта с ГОСТ Р 50779.30, ГОСТ Р 50779.50, ГОСТ Р 50779.53
Выбор планов контроля по настоящему стандарту основан на концепции AQL в отличие от концепции принципа распределения приоритетов (ПРП), использованной в ГОСТ Р 50779.30, ГОСТ Р 50779.50, ГОСТ Р 50779.53.
При использовании концепции AQL нормируется значение приемлемого уровня качества (несоответствий) AQL, при котором партии будут приниматься с высокой вероятностью. Отклонение партий с более высоким уровнем несоответствий зависит от уровня контроля и может быть определено по оперативной характеристике плана контроля.
При использовании концепции ПРП нормируется значение уровня качества (несоответствий) NQL, которое по определению является границей между удовлетворительным и неудовлетворительным качеством партий. При этом при контроле поставщика NQL играет роль браковочного уровня качества, а при контроле потребителя NQL играет роль приемлемого уровня качества AQL. Планы контроля поставщика и потребителя при этом различны, что обеспечивает практическое отсутствие спорных ситуаций (приемка партии у изготовителя и неприемка у потребителя). Планы контроля потребителя при этом близки к планам, выбираемым по концепции AQL.
При заключении договора (между поставщиком и потребителем) и выборе стандарта для планов контроля следует иметь в виду следующие факторы:
1) контроль по количественному признаку является более информативным и требует значительно меньших объемов выборок, чем контроль по альтернативному признаку, но требует знания закона распределения контролируемого показателя качества и более квалифицированного персонала;
2) стандарты на основе концепции AQL предпочтительно применять для контроля, проводимого потребителем. При использовании соответствующих планов контроля у поставщика потребитель не будет иметь гарантии того, что поступающая к нему продукция имеет фактический уровень качества не хуже AQL. Соответствующие планы контроля достаточно хорошо отсеивают только продукцию с фактическим качеством значительно хуже AQL;
3) Планы контроля изготовителя по концепции ПРП дают потребителю уверенность в фактическом качестве получаемой продукции не хуже NQL (уровень несоответствий - не выше NQL), но требуют, как правило, наличия «запаса по качеству» (более низкого фактического уровня несоответствий, чем NQL).
Ключевые слова: выборочный контроль качества партий продукции; стабильность процесса; нормальный закон распределения; количественный признак; приемлемый уровень качества; объем выборки; нормальный, усиленный, ослабленный контроль
|
|