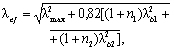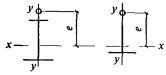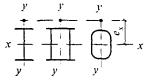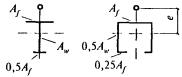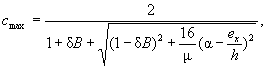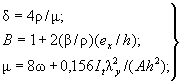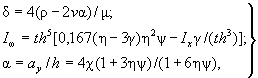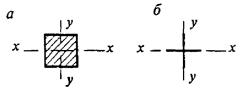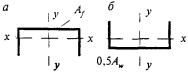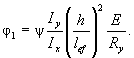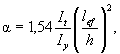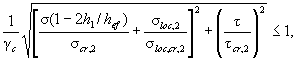|
||||||||||||||||||||||||
Система нормативных документов в строительстве
СВОД ПРАВИЛ
ПО ПРОЕКТИРОВАНИЮ И СТРОИТЕЛЬСТВУ
ОБЩИЕ ПРАВИЛА ПРОЕКТИРОВАНИЯ
СТАЛЬНЫХ КОНСТРУКЦИЙ
СП 53-102-2004
Москва 2005
ПРЕДИСЛОВИЕ
1 РАЗРАБОТАН Центральным научно-исследовательским институтом строительных конструкций им. В.А. Кучеренко (ЦНИИСК им. Кучеренко), Центральным научно-исследовательским институтом строительных металлоконструкций им. Н.П. Мельникова (ЗАО ЦНИИПСК им. Мельникова), Проектно-изыскательским и научно-исследовательским институтом по проектированию энергетических систем и электрических сетей (ОАО Институт «Энергосетьпроект») при участии группы специалистов
ВНЕСЕН Управлением технического нормирования, стандартизации и сертификации в строительстве и ЖКХ Госстроя России
2 ОДОБРЕН и рекомендован для применения на добровольной основе Госстроем России (письмо № ЛБ-2596/9 от 20.04.2004)
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ с 01.01.2005 г. приказом ЦНИИСК им. Кучеренко № 28/00 от 10.09.2004 г.
4 ВВЕДЕН ВПЕРВЫЕ
ВВЕДЕНИЕ
Настоящий Свод правил содержит рекомендуемые правила расчета и проектирования стальных строительных конструкций, обеспечивающие выполнение требований нормативных документов, распространяющихся на эти конструкции.
Решение вопроса о применении данного документа при проектировании стальных конструкций конкретного объекта относится к компетенции заказчика и разработчика проектной документации.
Если для реализации приняты методы расчета и проектирования, рекомендуемые настоящим документом, все установленные в нем правила должны соблюдаться в полном объеме.
В разработке настоящего Свода правил приняли участие: В.М. Горпинченко, д-р техн. наук, проф. - руководитель темы, В.М. Барышев, д-р техн. наук, Г.Е. Бельский, канд. техн. наук, И.И. Ведяков, д-р техн. наук, Л.А. Гильденгорн, канд. техн. наук, Л.Б. Кацнельсон, инж., П.Д. Одесский, д-р техн. наук, проф., В.А. Отставнов, канд. техн. наук, Ю.Н. Симаков, канд. техн. наук, М.Р. Урицкий, канд. техн. наук, Б.С. Цетлин, канд. техн. наук (ЦНИИСК им. Кучеренко); Л.И. Гладштейн, д-р техн. наук, И.Д. Грудев, д-р техн. наук, проф., Е.П. Морозов, канд. техн. наук, Н.Ю. Симон, канд. техн. наук (ЗАО ЦНИИПСК им. Мельникова); Е.Н. Колбанев (ОАО Институт «Энергосетьпроект»); Ю.И. Кудишин, д-р техн. наук, проф.; Ю.В. Соболев, канд.. техн. наук, проф., Б.Ю. Уваров, канд. техн. наук (МГСУ); В.И. Моисеев, д-р техн. наук, проф. (Электростальский политехнический институт МИСиС); А.Н. Евстратов, д-р техн. наук, проф., Б.А. Шемшура, канд. техн. наук (Шахтинский политехнический институт Южно-Российского государственного технического университета); С.Д. Шафрай, д-р техн. наук, проф. (Новосибирский Архитектурно-строительный университет им. Куйбышева); Ф.В. Бобров, канд. техн. наук (Управление технормирования Госстроя России).
СВОД ПРАВИЛ ПО ПРОЕКТИРОВАНИЮ И СТРОИТЕЛЬСТВУ
ОБЩИЕ ПРАВИЛА ПРОЕКТИРОВАНИЯ СТАЛЬНЫХ КОНСТРУКЦИЙ
General rules for steel structure design
Дата введения 2005-01-01
1 ОБЛАСТЬ ПРИМЕНЕНИЯ
Настоящий Свод правил распространяется на проектирование стальных строительных конструкций зданий и сооружений различного назначения, работающих при температуре окружающей среды не выше 100 °С и не ниже минус 65 °С. Свод правил не распространяется на проектирование стальных конструкций мостов, тоннелей и труб под насыпями.
При проектировании стальных конструкций, находящихся в особых условиях эксплуатации (например, конструкций доменных печей; магистральных и технологических трубопроводов; резервуаров специального назначения; конструкций зданий, подвергающихся сейсмическим воздействиям, интенсивным воздействиям огня, температуры, расплавленного металла, радиации, агрессивных сред; конструкций гидротехнических сооружений), конструкций уникальных зданий и сооружений, зданий атомных электростанций, а также специальных видов конструкций (например, предварительно напряженных, пространственных, висячих) кроме требований настоящего документа необходимо также соблюдать дополнительные требования, предусмотренные соответствующими нормативными документами, которые отражают особенности работы этих конструкций.
2 НОРМАТИВНЫЕ ССЫЛКИ
Перечень нормативных документов и стандартов, на которые имеются ссылки в настоящем Своде правил, приведен в приложении А.
3 ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ
В настоящем Своде правил использованы термины, определения которых содержатся в нормативных документах, на которые в тексте имеются ссылки.
4 ОБОЗНАЧЕНИЯ
В настоящем Своде правил использованы буквенные обозначения величин, индексы буквенных обозначений и поясняющие их слова, приведенные в приложении Б.
5 ОБЩИЕ ПОЛОЖЕНИЯ
5.1 ОСНОВНЫЕ ТРЕБОВАНИЯ К КОНСТРУКЦИЯМ
5.1.1 При проектировании стальных конструкций:
следует соблюдать требования государственных стандартов на конструкции соответствующего вида, а также других нормативных документов (приложение А);
при необходимости следует выполнять расчет точности геометрических параметров конструкций и их элементов согласно ГОСТ 21780.
5.1.2 При проектировании стальных конструкций следует соблюдать требования к огнестойкости и коррозионной стойкости согласно СНиП 21-01 и СНиП 2.03.11.
Все конструкции, не замоноличенные в бетоне, не заделанные в кирпичной кладке и т.п., должны быть доступны для наблюдения, очистки, окраски, а также не должны задерживать влагу и затруднять проветривание. Замкнутые профили должны быть герметизированы.
5.1.3 За расчетную температуру наружного воздуха принимается температура воздуха наиболее холодных суток обеспеченностью 0,98, определенная согласно СНиП 23-01.
Расчетные технологические температуры устанавливаются заданием на разработку строительной части проекта.
5.1.4 Проектирование конструкций должно осуществляться квалифицированными специалистами. Рабочие чертежи стальных конструкций должны соответствовать требованиям по изготовлению (ГОСТ 23118) и монтажу конструкций (СНиП 3.03.01).
В необходимых случаях при заказе стали указывается класс сплошности по ГОСТ 27772.
5.2 ОСНОВНЫЕ РАСЧЕТНЫЕ ТРЕБОВАНИЯ
5.2.1 Надежность стальных конструкций обеспечивается в соответствии с требованиями ГОСТ 27751.
Расчет стальных конструкций выполняется с учетом назначения конструкций, условий их изготовления, транспортировки, монтажа и эксплуатации, а также свойств материалов.
5.2.2 Значения нагрузок и воздействий, а также предельные значения прогибов и перемещений элементов конструкций принимаются согласно требованиям СНиП 2.01.07.
5.2.3 При проектировании зданий и сооружений принимаются конструктивные схемы, обеспечивающие прочность, устойчивость и пространственную неизменяемость зданий и сооружений в целом и их отдельных элементов при транспортировании, монтаже и эксплуатации.
5.2.4 Расчетные схемы и основные предпосылки расчета должны отражать действительные условия работы стальных конструкций.
Стальные конструкции следует, как правило, рассчитывать как единые пространственные системы с учетом факторов, определяющих напряженное и деформированное состояние, особенности взаимодействия элементов конструкций между собой и с основанием, геометрической и физической нелинейности, свойств материалов и грунтов.
Допускается выполнять проверку устойчивости стержневых конструкций (в том числе пространственных) с использованием сертифицированных вычислительных комплексов как идеализированных систем в предположении упругих деформаций стали по недеформированной схеме.
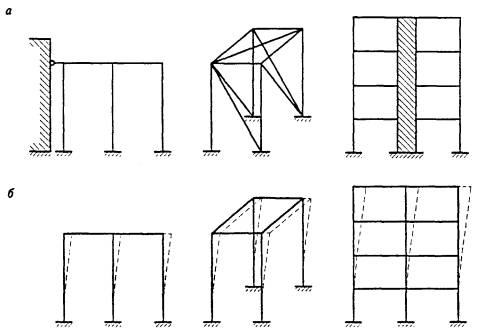
5.2.5 Рассматриваются следующие расчетные модели несущих конструкций:
- отдельные конструктивные элементы (например, растянутые и сжатые стержни, балки, стойки и колонны сплошного сечения и др.);
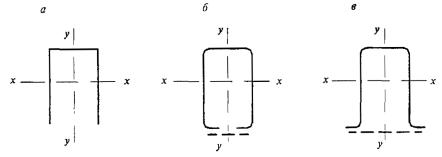
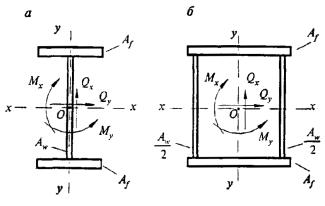
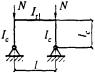
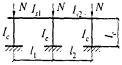
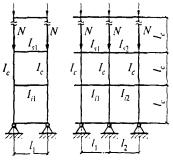
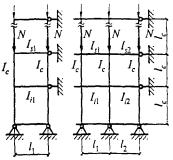
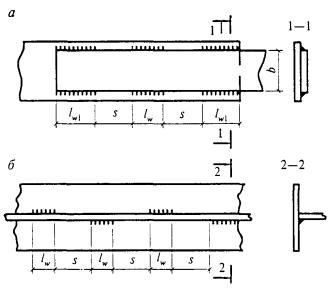
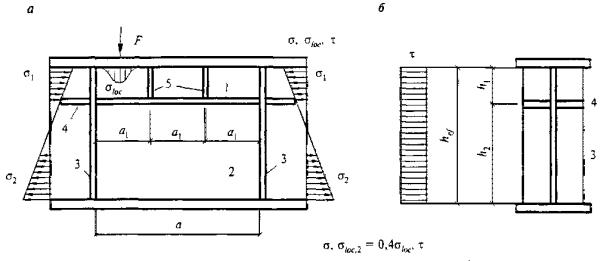
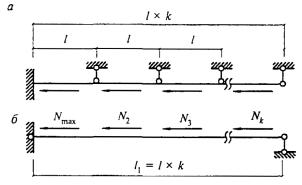
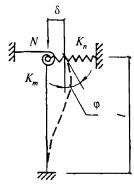
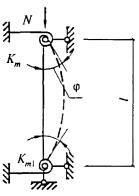
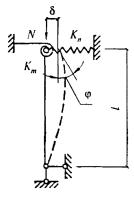
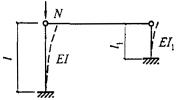
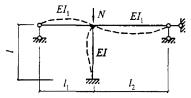
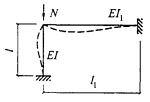
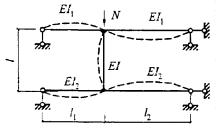
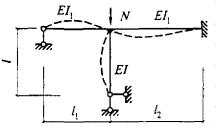
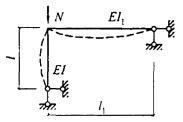
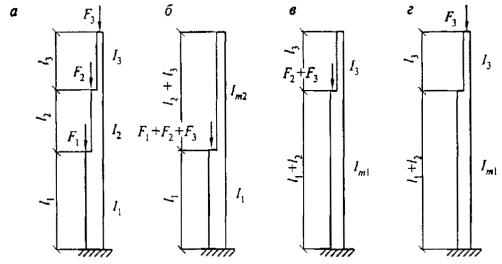
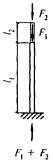
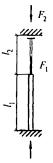
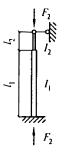
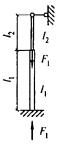
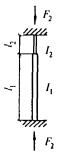
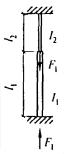
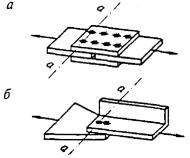
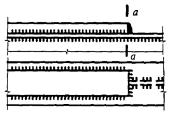
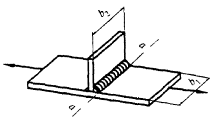
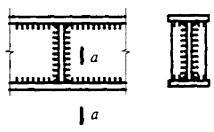
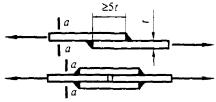
- плоские или пространственные системы, закрепленные от перекоса (рисунок 1, а); расчет таких конструкций может быть выполнен путем расчета отдельных элементов с учетом их взаимодействия между собой и с основанием;
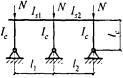
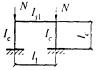
- плоские или пространственные системы, не закрепленные от перекосов (рисунок 1, б); при расчете таких конструкций наряду с проверкой отдельных элементов следует учитывать возможность достижения предельного состояния системы в целом;
- листовые конструкции (оболочки вращения).
Рисунок 1 - Схемы систем, закрепленных (а) и не закрепленных (б) от перекоса
5.2.6 Элементы конструкций, рассматриваемые в настоящем Своде правил, подразделяются на три класса в зависимости от напряженно-деформированного состояния (НДС) расчетного сечения:
1-й класс - НДС, при котором напряжения в сечении не превышают расчетного сопротивления стали σ ≤ Ry (упругая работа сечения);
2-й класс - НДС, при котором в одной части сечения σ < Ry, а в другой σ = Ry (упругопластическая работа сечения);
3-й класс - НДС, при котором по всей площади сечения σ = Ry (пластификация всего сечения, условный пластический шарнир).
5.2.7 Для элементов, ослабленных отверстиями для болтовых соединений, кроме фрикционных, при расчетах на прочность и усталость принимают сечения нетто (An), а на устойчивость и жесткость - сечения брутто (A).
Для элементов с фрикционными соединениями при расчетах на усталость, устойчивость и жесткость принимают сечение брутто (A), а при расчете на прочность - расчетное сечение (Ad) с учетом сил трения.
5.3 УЧЕТ НАЗНАЧЕНИЯ И УСЛОВИЙ РАБОТЫ КОНСТРУКЦИЙ
5.3.1 При расчете конструкций и соединений учитывают:
коэффициенты надежности по ответственности γn, принимаемые согласно требованиям обязательного приложения 7* «Учет ответственности зданий и сооружений» к СНиП 2.01.07;
коэффициент надежности в расчетах по временному сопротивлению γu = 1,3 для элементов конструкций, рассчитываемых на прочность с использованием расчетных сопротивлений Ru;
коэффициент надежности по устойчивости γs = 1,3 для стержневых конструкций, рассчитываемых как идеализированные пространственные системы с использованием сертифицированных вычислительных комплексов (согласно 5.2.4), на него следует умножать значения расчетных нагрузок;
коэффициенты условий работы элементов конструкций и соединений γc, γc1 и γb, принимаемые по таблице 1, а также согласно требованиям разделов 8, 15, 17, 18, 19 настоящего Свода правил.
Таблица 1
|
№ п.п. |
Элементы конструкций |
Коэффициент условий работы γc |
|
1 |
Балки сплошного сечения и сжатые элементы ферм перекрытий под залами театров, клубов, кинотеатров, под трибунами, под помещениями магазинов, книгохранилищ и архивов и т.п. при временной нагрузке, не превышающей вес перекрытий |
0,90 |
|
2 |
Колонны общественных зданий и опор водонапорных башен |
0,95 |
|
3 |
Колонны одноэтажных производственных зданий с мостовыми кранами |
1,05 |
|
4 |
Сжатые основные элементы (кроме опорных) решетки составного таврового сечения из двух уголков в сварных фермах покрытий и перекрытий при расчете на устойчивость указанных элементов с гибкостью λ > 60 |
0,80 |
|
5 |
Растянутые элементы (затяжки, тяги, оттяжки, подвески) при расчете на прочность по неослабленному сечению |
0,90 |
|
6 |
Элементы конструкций из стали с пределом текучести до 440 Н/м2, несущие статическую нагрузку, при расчете на прочность по сечению, ослабленному отверстиями для болтов (кроме фрикционных соединений) |
1,10 |
|
7 |
Сжатые элементы решетки пространственных решетчатых конструкций из одиночных уголков, прикрепляемых одной полкой (для неравнополочных уголков большой полкой): |
|
|
непосредственно к поясам сварными швами либо двумя болтами и более, поставленными вдоль уголка: |
|
|
|
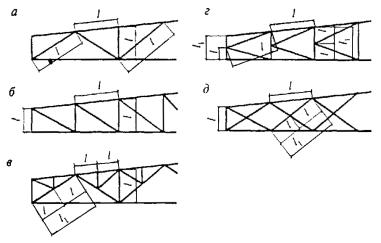
раскосы по рисунку 13, а |
0,90 |
|
|
распорки по рисунку 13, б, в, е |
0,90 |
|
|
раскосы по рисунку 13, в, г, д, е |
0,80 |
|
|
непосредственно к поясам одним болтом или через фасонку независимо от вида соединения |
0,75 |
|
|
8 |
Сжатые элементы из одиночных уголков, прикрепляемых одной полкой (для неравнополочных уголков меньшей полкой), за исключением элементов плоских ферм из одиночных уголков и элементов, указанных в позиции 6 настоящей таблицы, раскосов по рисунку 13, б, прикрепляемых непосредственно к поясам сварными швами либо двумя болтами и более, поставленными вдоль уголка |
0,75 |
|
9 |
Опорные плиты из стали с пределом текучести до 390 Н/мм2, несущие статическую нагрузку, толщиной, мм: |
|
|
до 40 |
1,20 |
|
|
св. 40 до 60 |
1,15 |
|
|
» 60 » 80 |
1,10 |
|
|
Примечания 1 Коэффициенты γc < 1 при расчете совместно не учитывают. 2 При расчете на прочность по сечению, ослабленному отверстиями для болтов, коэффициенты, приведенные в позициях 6 и 1, 6 и 2, 6 и 3, учитывают совместно. 3 При расчете опорных плит коэффициенты, приведенные в позициях 9 и 2, 9 и 3, учитывают совместно. 4 Коэффициенты, приведенные в позициях 1 и 2, учитывают при расчете соединений рассматриваемых элементов. 5 В случаях, не оговоренных в настоящем Своде правил, в формулах принимают γc = 1. |
||
5.3.2 При проектировании конструкций, подвергающихся непосредственному воздействию подвижных, вибрационных и других переменных нагрузок, вызывающих усталость металла, учитывают требования к материалу, конструированию и технологии изготовления, а в случаях, указанных в настоящем Своде правил, выполняют расчет на усталость.
5.3.3 При проектировании конструкций, возводимых или эксплуатируемых в условиях низких температур, при которых повышается возможность хрупкого разрушения, учитывают требования к материалу, конструированию и технологии изготовления.
5.3.4 При проектировании сварных конструкций снижают вредное влияние остаточных деформаций и напряжений, в том числе сварочных, а также концентрации напряжений, предусматривая соответствующие конструктивные решения (с наиболее равномерным распределением напряжений в элементах и деталях, без входящих углов, резких перепадов сечения и других концентраторов напряжений) и технологические мероприятия (порядок сборки и сварки, предварительный выгиб, механическую обработку соответствующих зон путем строжки, фрезерования, зачистки абразивным кругом и др.).
6 МАТЕРИАЛЫ ДЛЯ КОНСТРУКЦИЙ И СОЕДИНЕНИЙ
6.1 Стали для конструкций применяют согласно требованиям приложения В (в том числе приведенным в таблицах В.1 и В.2).
6.2 Для конструкций используют фасонный (уголки, двутавры, швеллеры), листовой, широкополосный универсальный прокат и гнутые профили с техническими требованиями по ГОСТ 27772, тонколистовой прокат из углеродистой стали по ГОСТ 16523, из стали повышенной прочности - по ГОСТ 17066, холодногнутые профили по ГОСТ 11474, профили гнутые замкнутые квадратные и прямоугольные по ГОСТ 30245, сортовой прокат (круг, квадрат, полоса) по ГОСТ 535 и ГОСТ 19281, электросварные трубы по ГОСТ 10705 и ГОСТ 10706, горячекатаные трубы по ГОСТ 8731. Может быть также использован прокат, выпускаемый по другим стандартам и ТУ в соответствии с Правилами по выбору стали для металлических конструкций, разработанными ЦНИИСК им. Кучеренко.
Листовой прокат толщиной 25 мм и более для элементов, работающих на растяжение в направлении толщины, и остальной прокат толщиной более 40 мм должны удовлетворять требованиям ГОСТ 28870 по свойствам в направлении толщины (Z-свойствам).
В качестве стали повышенной огнестойкости применяется прокат по ТУ 14-1-5399-2000. Открытые конструкции из этого проката имеют предел огнестойкости R = 45 мин. Прокат должен иметь нормативное значение временного сопротивления при температуре 600 °С не менее Run = 240 Н/мм2.
6.3 Для отливок (опорных частей и т.д.) применяют сталь марок 15Л, 25Л, 35Л и 45Л, удовлетворяющую требованиям ГОСТ 977 для групп II (отливки ответственного назначения для деталей, рассчитываемых на прочность, работающих при статических и переменных нагрузках) или III (отливки особо ответственного назначения для деталей, рассчитываемых на прочность, работающих при динамических нагрузках).
6.4 Для сварки применяют материалы: электроды для ручной дуговой сварки по ГОСТ 9467, сварочную проволоку по ГОСТ 2246, флюсы по ГОСТ 9087, порошковую проволоку по ГОСТ 26271 согласно таблице Г.1 приложения Г, а также углекислый газ по ГОСТ 8050, аргон по ГОСТ 10157. Применяемые сварочные материалы и технология сварки должны обеспечивать значение временного сопротивления металла шва не ниже нормативного значения временного сопротивления Run основного металла, а также значения твердости, ударной вязкости и относительного удлинения металла сварных соединений, установленные соответствующими нормативными документами.
6.5 Для болтовых соединений применяют стальные болты и гайки, удовлетворяющие техническим требованиям ГОСТ 1759.0, ГОСТ 1759.4, ГОСТ 1759.5, шайбы, удовлетворяющие требованиям ГОСТ 18123, и высокопрочные болты, указанные в 6.8.
Болты применяют согласно требованиям таблицы Г.3 приложения Г.
Класс прочности гайки принимается, как правило, в соответствии с классом прочности болтов: 5 - при 5,6; 8 - при 8,8; 10 - при 10,9; 12 - при 12,9.
При работе болтов только на срез допускается применять класс прочности гаек при классе прочности болтов: 4 - при 5,6; 6 - при 8,8; 8 - при 10,9; 10 - при 12,9.
Шайбы применяют: круглые с техническими требованиями по ГОСТ 11371, косые - по ГОСТ 10906, пружинные нормальные - по ГОСТ 6402.
6.6 Для фундаментных болтов применяют стальные болты, удовлетворяющие требованиям ГОСТ 24379.0 и требованиям, приведенным в таблице Г.4 приложения Г.
6.7 Гайки для фундаментных и U-образных болтов диаметром до 48 мм применяют по техническим требованиям ГОСТ 5915, свыше 48 мм - по ГОСТ 10605. Для фундаментных болтов из стали Ст3пс2, Ст3сп2, Ст3пс4, Ст3сп4 диаметром до 48 мм применяют гайки класса прочности 4 по ГОСТ 1759.5, диаметром свыше 48 мм - из материала не ниже группы 02 по ГОСТ 18126.
Для фундаментных болтов диаметром до 48 мм из стали марки 09Г2С и других сталей по ГОСТ 19281 применяют гайки класса прочности не ниже 5 по ГОСТ 1759.5, диаметром свыше 48 мм - из материала не ниже группы 05 по ГОСТ 18126. Допускается применять гайки из стали марок, применяемых для болтов.
6.8 Для фрикционных соединений применяют высокопрочные болты из стали 40Х «селект», удовлетворяющие требованиям ГОСТ 22356, а их конструкцию и размеры принимают по ГОСТ 22353, гайки и шайбы к ним - по ГОСТ 22354 и ГОСТ 22355.
6.9 Для фланцевых соединений применяют высокопрочные болты из стали 40Х «селект» с временным сопротивлением не менее 1100 Н/мм2 в исполнении ХЛ, удовлетворяющие требованиям ГОСТ 22356; гайки и шайбы к ним - по ГОСТ 22354 и ГОСТ 22355.
6.10 Для несущих элементов висячих покрытий, оттяжек опор воздушных линий электропередачи, распределительных устройств, контактных сетей транспорта, мачт и башен, а также напрягаемых элементов в предварительно напряженных конструкциях применяют:
канаты спиральные по ГОСТ 3062, ГОСТ 3063, ГОСТ 3064;
канаты двойной свивки по ГОСТ 3066, ГОСТ 3067, ГОСТ 3068, ГОСТ 3081, ГОСТ 7669, ГОСТ 14954;
канаты закрытые несущие по ГОСТ 3090, ГОСТ 7675, ГОСТ 7676, ГОСТ 18901;
пучки и пряди параллельных проволок, формируемых из канатной проволоки, удовлетворяющей требованиям ГОСТ 7372.
6.11 Физические характеристики материалов, применяемых для стальных конструкций, принимают согласно приложению Д.
7 РАСЧЕТНЫЕ ХАРАКТЕРИСТИКИ МАТЕРИАЛОВ И СОЕДИНЕНИЙ
7.1 Расчетные сопротивления проката, гнутых профилей и труб определяют по формулам, приведенным в таблице 2, где нормативные сопротивления Ryn и Run принимают согласно стандартам и техническим условиям, а коэффициент надежности по материалу γm - согласно таблице 3.
Нормативные и расчетные сопротивления листового, широкополосного универсального, фасонного проката и труб приведены в таблицах В.5, В.6, В.7 приложения В.
7.2 Расчетные сопротивления гнутых профилей принимают равными расчетным сопротивлениям листового проката, из которого они изготовлены; допускается учитывать упрочнение стали в зоне гиба.
7.3 Расчетные сопротивления отливок из углеродистой стали приведены в таблице В.8 приложения В.
7.4 Расчетные сопротивления сварных соединений определяют по формулам, приведенным в таблице 4.
Таблица 2
|
Напряженное состояние |
Условное обозначение |
Расчетное сопротивление проката и труб |
|
Растяжение, сжатие, изгиб: |
|
|
|
по пределу текучести |
Ry |
Ry = Ryn/γm |
|
по временному сопротивлению |
Ru |
Ru = Run/γm |
|
Сдвиг |
Rs |
Rs = 0,58Ryn/γm |
|
Смятие: |
|
|
|
торцевой поверхности (при наличии пригонки) |
Rp |
Rp = Run/γm |
|
местное в цилиндрических шарнирах (цапфах) при плотном касании |
Rlp |
Rlp = 0,5Run/γm |
|
Диаметральное сжатие катков (при свободном касании в конструкциях с ограниченной подвижностью) |
Rcd |
Rcd = 0,025Run/γm |
Таблица 3
|
Государственный стандарт или технические условия на прокат и трубы |
Коэффициент надежности по материалу γm |
|
ГОСТ 27772 (кроме сталей С590 и С590К) и другая нормативная документация, использующая процедуру контроля свойств проката по ГОСТ 27772 |
1,025 |
|
Для сортового проката с пределом текучести свыше 380 Н/мм2 по ГОСТ 19281, для труб - по ГОСТ 8731 |
1,100 |
|
Для остального проката и труб, соответствующих требованиям настоящего Свода правил |
1,050 |
Таблица 4
|
Сварное соединение |
Напряженное состояние |
Характеристика расчетного сопротивления |
Условное обозначение |
Расчетное сопротивление сварного соединения |
|
Стыковое |
Сжатие, растяжение и изгиб при механизированной или ручной сварке с физическим контролем качества шва |
По пределу текучести |
Rwy |
Rwy = Ry |
|
По временному сопротивлению |
Rwu |
Rwu = Ru |
||
|
Растяжение и изгиб при механизированной или ручной сварке |
По пределу текучести |
Rwy |
Rwy = 0,85Ry |
|
|
Сдвиг |
Rws |
Rws = Rs |
||
|
С угловыми швами |
Срез (условный) |
По металлу шва |
Rwf |
Rwf = Rwun/γwm |
|
По металлу границы сплавления |
Rwz |
Rwz = 0,45Run |
||
|
Примечание - Значения коэффициента надежности по металлу шва γwm принимают равными: 1,25 - при Rwun ≤ 490 Н/мм2; 1,35 - при Rwun ≥ 590 Н/мм2. |
||||
Расчетные сопротивления стыковых соединений из сталей с разными нормативными сопротивлениями принимают как для стыковых соединений из стали с меньшим значением нормативного сопротивления.
Нормативные (Rwun) и расчетные (Rwf) сопротивления металла угловых швов приведены в таблице Г.2 приложения Г.
7.5 Расчетные сопротивления одноболтовых соединений определяют по формулам, приведенным в таблице 5.
Расчетные сопротивления срезу и растяжению болтов, а также смятию элементов, соединяемых болтами, приведены в таблицах Г.5 и Г.6 приложения Г.
7.6 Расчетное сопротивление растяжению фундаментных болтов Rba определяют по формуле
Rba = 0,8Ryn (1)
и принимают согласно таблице Г.7 приложения Г.
Расчетное сопротивление растяжению U-образных болтов, указанных в 6.6, определяют по формуле
RbU = 0,85Ryn (2)
и принимают согласно таблице Г.7 приложения Г.
7.7 Расчетное сопротивление растяжению высокопрочных болтов Rbh определяют по формуле
Rbh = 0,7Rbun, (3)
где Rbun - нормативное сопротивление болта, принимаемое согласно таблице Г.8 приложения Г.
7.8 Расчетное сопротивление растяжению высокопрочной стальной проволоки Rdh, применяемой в виде пучков или прядей, определяют по формуле
Rdh = 0,63Run. (4)
7.9 Значение расчетного сопротивления (усилия) растяжению стального каната принимают равным значению разрывного усилия каната в целом, установленному государственными стандартами или техническими условиями на стальные канаты, деленному на коэффициент надежности по материалу γm = 1,6.
8 РАСЧЕТ ЭЛЕМЕНТОВ СТАЛЬНЫХ КОНСТРУКЦИЙ ПРИ ЦЕНТРАЛЬНОМ РАСТЯЖЕНИИ И СЖАТИИ
8.1 РАСЧЕТ ЭЛЕМЕНТОВ СПЛОШНОГО СЕЧЕНИЯ
8.1.1 Расчет на прочность элементов из стали с нормативным сопротивлением Ryn ≤ 440 Н/мм2 при центральном растяжении и сжатии выполняют по формуле
Расчет на прочность растянутых элементов, эксплуатация которых возможна и после достижения металлом предела текучести, а также растянутых и сжатых элементов из стали с нормативным сопротивлением Ryn > 440 Н/мм2 выполняют по формуле (5) с заменой значения Ry на Ru/γu.
Расчет на прочность элементов в сечении с нарезкой для гайки выполняют как расчет болта на растяжение (по 15.29).
Таблица 5
8.1.2 Расчет на прочность сечений в местах крепления растянутых элементов из одиночных уголков, прикрепляемых одной полкой болтами, выполняют по формуле (5) и по формуле
где γc1 - коэффициент условий работы, определяемый согласно приложению Е.
8.1.3 Расчет на устойчивость элементов сплошного сечения при центральном сжатии и при удовлетворении требований 8.3.2 - 8.3.9 выполняют по формуле
где φ - коэффициент устойчивости при центральном
сжатии, значение которого при ![]() вычисляют по формуле
вычисляют по формуле
Значение коэффициента δ в формуле (8) вычисляют по формуле
δ = 9,87(1 - α + β![]() ) +
) + ![]() , (9)
, (9)
где ![]() - условная гибкость стержня;
- условная гибкость стержня;
α и β - коэффициенты, определяемые по таблице 6 в зависимости от типов сечений для различных типов кривых устойчивости.
Таблица 6
|
Тип кривой устойчивости |
Значения коэффициентов |
||
|
α |
β |
||
|
|
a |
0,03 |
0,06 |
|
|
b |
0,04 |
0,09 |
|
|
c |
0,04 |
0,14 |
|
Примечание - Для прокатных двутавров высотой свыше 500 мм при расчете на устойчивость в плоскости стенки принимают тип кривой устойчивости a. |
|||
Значения
коэффициента φ, вычисленные по формуле (8),
принимают не более ![]() при значениях
условной гибкости свыше 3,8; 4,4 и 5,8 для типов кривой
устойчивости соответственно a, b и c.
при значениях
условной гибкости свыше 3,8; 4,4 и 5,8 для типов кривой
устойчивости соответственно a, b и c.
При значениях ![]() для всех типов кривой
устойчивости допускается принимать φ = 1.
для всех типов кривой
устойчивости допускается принимать φ = 1.
Значения коэффициента φ приведены в приложении Ж.
8.1.4 Расчет на устойчивость стержней из одиночных уголков выполняют с учетом требований 8.1. При определении гибкости этих стержней радиус инерции сечения уголка и расчетную длину принимают согласно требованиям 11.1 и 11.2.1.
При расчете поясов и элементов решетки пространственных конструкций из одиночных уголков выполняют требования 17.10 настоящего Свода правил.
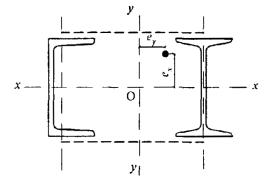
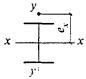
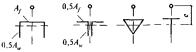
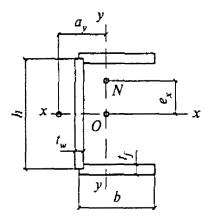
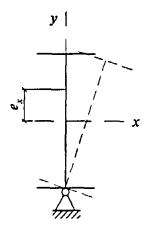
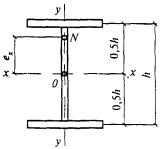
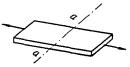
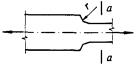
8.1.5 Сжатые элементы со сплошными стенками открытого П-образного сечения (рисунок 2) укрепляют планками или решеткой, при этом выполняют требования 8.2.1 - 8.2.9.
При отсутствии планок или решеток такие элементы, помимо расчета по формуле (7) в главных плоскостях х-х и у-у, проверяют на устойчивость при изгибно-крутильной форме потери устойчивости по формуле
![]() (10)
(10)
здесь φc - коэффициент, принимаемый равным:
φc = φ1, при φ1 ≤ 0,85;
φc = 0,68 + 0,21φ1 ≤ 1 при φ1 > 0,85,
где значение φ1 вычисляют по формуле
В формуле (11) коэффициент cmax определяют согласно приложению И.
8.1.6 Соединение пояса со стенкой в центрально-сжатом элементе составного сплошного сечения рассчитывают по формулам таблицы 40 на сдвиг от условной поперечной силы Qfic, определяемой по формуле (18).
8.2 РАСЧЕТ ЭЛЕМЕНТОВ СКВОЗНОГО СЕЧЕНИЯ
8.2.1 Расчет на прочность элементов сквозного сечения при центральном растяжении и сжатии выполняют по формуле (5), где An - площадь сечения нетто всего стержня.
8.2.2 Расчет на устойчивость сжатых стержней сквозного сечения, ветви которых соединены планками или решетками, выполняют по формуле (7); при этом коэффициент φ относительно свободной оси
(перпендикулярной плоскости планок или решеток) определяют по формулам (8) и (9) для кривой устойчивости типа b с заменой в них ![]() на
на ![]() . Значение
. Значение ![]() определяют в зависимости от
значений
определяют в зависимости от
значений ![]() , приведенных в таблице 7 для стержней с числом панелей, как правило, не менее шести.
, приведенных в таблице 7 для стержней с числом панелей, как правило, не менее шести.
Расчет на устойчивость сквозных стержней с числом панелей менее шести допускается выполнять:
при планках - как расчет рамных систем;
при решетках - согласно требованиям 8.2.5.
8.2.3 В сквозных стержнях с
планками условная гибкость отдельной ветви ![]() ,
, ![]() или
или ![]() (таблица 7) на участке
между сварными швами или крайними болтами, прикрепляющими планки, должна быть не более 1,4.
(таблица 7) на участке
между сварными швами или крайними болтами, прикрепляющими планки, должна быть не более 1,4.
При наличии в одной из плоскостей сплошного листа вместо планок (рисунок 2, б, в) гибкость ветви вычисляют по радиусу инерции полусечения относительно его центральной оси, перпендикулярной плоскости планок.
8.2.4 В сквозных стержнях с решетками помимо расчета на устойчивость стержня в целом проверяют устойчивость отдельных ветвей на участках между узлами. При необходимости учитывают влияние моментов в узлах, например от расцентровки элементов решетки.
В сквозных стержнях с решетками условная гибкость отдельных ветвей
между узлами, как правило, должна быть не более 2,7 и не должна превышать условную приведенную гибкость ![]() стержня в
целом.
стержня в
целом.
Допускается принимать более высокие значения условной гибкости ветвей, но не более 4,1, при условии, что расчет таких стержней выполнен согласно требованиям 8.2.5.
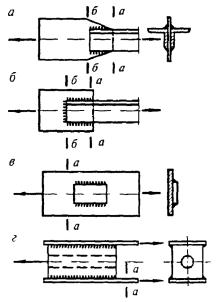
а - открытое; б, в - укрепленные планками или решетками
Рисунок 2 - П-образные сечения элементов
Таблица 7
|
Схема сечения |
Приведенная гибкость λef стержни сквозного сечения |
||
|
с планками |
с решетками |
||
|
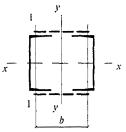
1 |
|
где |
где |
|
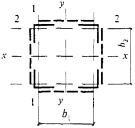
2 |
|
где
|
где
(d1 и d2 относятся к сторонам соответственно b1 и b2). |
|
3 |
|
где |
где |
|
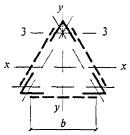
Обозначения, принятые в таблице 7: λy - гибкость сквозного стержня в плоскости, перпендикулярной оси у-у; λmax - наибольшая из гибкостей сквозного стержня в плоскостях, перпендикулярных осям х-х или y-y, равная соответственно lx/ix или ly/iy (где ix, iy - радиусы инерции сечения сквозного стержня в целом); λb1, λb2, λb3 - гибкости отдельных ветвей при изгибе в плоскостях, перпендикулярных осям соответственно 1-1, 2-2 и 3-3, на участках между сварными швами или крайними болтами, прикрепляющими планки; b, d, lb - размеры, определяемые по рисункам 3 и 4; A - площадь сечения всего стержня; Ad1, Ad2, Ad3 - площади поперечных сечений раскосов решеток, расположенных соответственно в плоскостях, перпендикулярных осям 1-1, 2-2 и параллельных оси 3-3 (при крестовой решетке - двух раскосов); Ib1, Ib3 - моменты инерции сечения ветвей относительно осей соответственно 1-1 и 3-3 (для сечений типов 1 и 3); Ib1, Ib2 - то же, двух уголков относительно осей соответственно 1-1 и 2-2 (для сечения типа 2); Is - момент инерции сечения одной планки относительно собственной оси х-х (рисунок 4; для сечений типов 1 и 3); Is1, Is2 - момент инерции сечения одной из планок, расположенных в плоскостях, перпендикулярных осям соответственно 1-1 и 2-2 (для сечения типа 2). Примечание - К типу 1 относят также сечения, у которых вместо швеллеров применены двутавры, трубчатые и другие профили для одной или обеих ветвей; при этом оси y-y и 1-1 должны проходить через центры тяжести соответственно сечения в целом и отдельной ветви, а значения n и λb1 в формуле (12) должны обеспечить наибольшее значение λef. |
|||
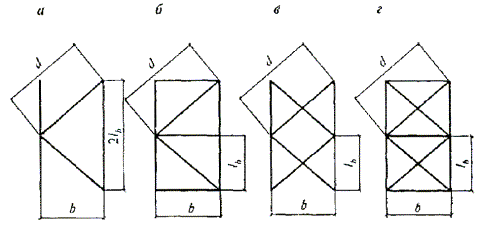
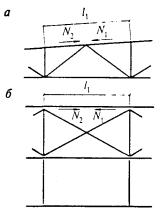
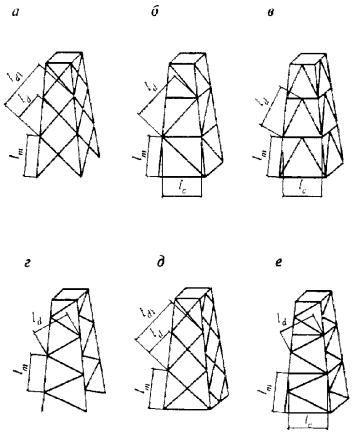
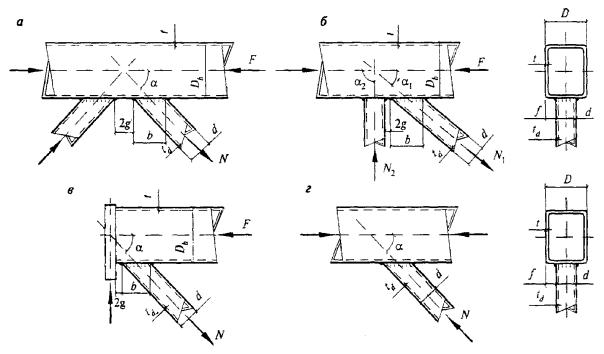
а - треугольная; б - треугольная с распорками; в - крестовая; г - крестовая с распорками
Рисунок 3 - Схемы раскосных решеток сквозных стержней
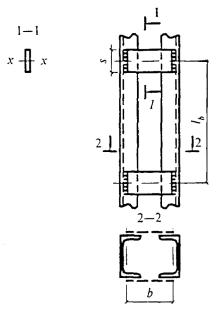
Рисунок 4 - Сквозной стержень с планками
8.2.5 Расчет сквозных стержней с решетками при учете указанных в 8.2.2 - 8.2.4 допущений выполняют по формулам (7) и (8) с заменой в них значения Ry на Ryd = φ1Ry.
При этом коэффициент устойчивости φ1 для отдельной ветви при ![]() принимают равным 1,0, а при
принимают равным 1,0, а при ![]() определяют по формулам (7) и (8) при расчетной длине lef = 0,7lb (где lb - длина ветви; на рисунке 3,
а длина ветви 2lb).
определяют по формулам (7) и (8) при расчетной длине lef = 0,7lb (где lb - длина ветви; на рисунке 3,
а длина ветви 2lb).
В интервале условных гибкостей ![]() для φ1 допускается линейная интерполяция между 1,0 и значением φ1 при
для φ1 допускается линейная интерполяция между 1,0 и значением φ1 при ![]() .
.
8.2.6 Расчет составных элементов из уголков, швеллеров и др., соединенных вплотную или через прокладки, выполняют как сплошностенчатых при условии, что участки между соединяющими сварными швами или центрами крайних болтов не превышают для сжатых элементов 40i и для растянутых 80i. Здесь радиус инерции сечения i уголка или швеллера принимают для тавровых или двутавровых сечений относительно оси, параллельной плоскости расположения прокладок, а для крестовых сечений - минимальный.
При этом в пределах длины сжатого элемента предусматривают не менее двух промежуточных связей (прокладок).
8.2.7 Расчет соединительных планок и элементов решеток сжатых стержней сквозного сечения выполняют на условную поперечную силу Qfic, принимаемую постоянной по всей длине стержня и определяемую по формуле
Qfic = 7,15 · 10-6(2330 - E/Ry)N/φ, (18)
где N - продольное усилие в составном стержне;
φ - коэффициент устойчивости при центральном сжатии, принимаемый при расчете сквозного стержня в плоскости планок или решеток.
Условную поперечную силу Qfic принимают:
при наличии только соединительных планок (решеток) - распределенной поровну между планками (решетками), лежащими в плоскостях, перпендикулярных оси, относительно которой производится проверка устойчивости;
при наличии сплошного листа и соединительных планок (решеток) - распределенной поровну между листом и планками (решетками), лежащими в плоскостях, параллельных листу;
при расчете равносторонних трехгранных сквозных стержней - равной 0,8Qfic для каждой системы соединительных планок (решеток), расположенной в одной грани.
8.2.8 Расчет соединительных планок и их прикреплений (рисунок 4) выполняют как расчет элементов безраскосных ферм на совместное действие силы Fs, срезывающей планку, и момента Ms, изгибающего планку в ее плоскости, значения которых определяют по формулам:
Fs = Qslb/b; (19)
Ms = Qslb/2, (20)
где Qs - условная поперечная сила, приходящаяся на планку одной грани.
8.2.9 Расчет элементов соединительных решеток составных стержней выполняют как расчет элементов решеток плоских ферм; для решеток по рисунку 3 усилие в раскосе определяют по формуле
Nd = α1Qsd/b, (21)
где α1 - коэффициент, принимаемый равным: 1 для решетки по рисунку 3, а, б и 0,5 - по рисунку 3, в;
Qs - условная поперечная сила, приходящаяся на одну плоскость решетки.
При расчете раскосов крестовой решетки с распорками (рисунок 3, г) учитывают дополнительное усилие Nad, возникающее в каждом раскосе от обжатия ветвей и определяемое по формуле
Nad = α2NbAd/Ab, (22)
где α2 = dlb2/(2b3 + d3) - коэффициент, вычисляемый по размерам b, lb, d, указанным на рисунке 3;
Nb - усилие в одной ветви стержня;
Ad, Ab - площадь сечения соответственно раскоса и ветви.
8.2.10 Расчет стержней, предназначенных для уменьшения расчетной длины сжатых элементов, выполняют на усилие, равное условной поперечной силе в основном сжатом элементе, определяемой по формуле (18).
Расчет распорок, предназначенных для уменьшения расчетной длины колонн в плоскости, перпендикулярной плоскости поперечных рам, при наличии нагрузок от мостовых или подвесных кранов выполняют на условную поперечную силу, определяемую по формуле (17), где значение N принимается равным сумме продольных сил в двух колоннах, соединенных распоркой.
8.3 ПРОВЕРКА УСТОЙЧИВОСТИ СТЕНОК И ПОЯСНЫХ ЛИСТОВ ЦЕНТРАЛЬНО-СЖАТЫХ ЭЛЕМЕНТОВ СПЛОШНОГО СЕЧЕНИЯ
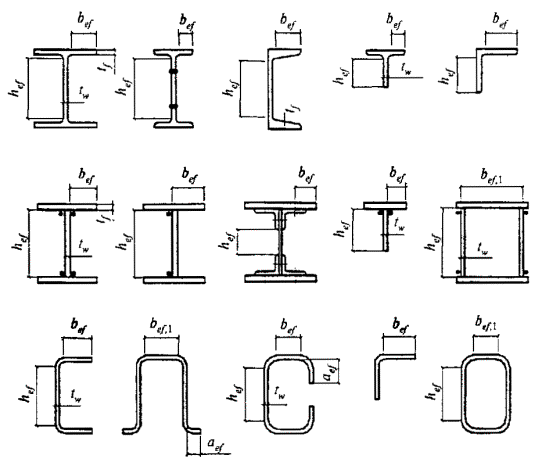
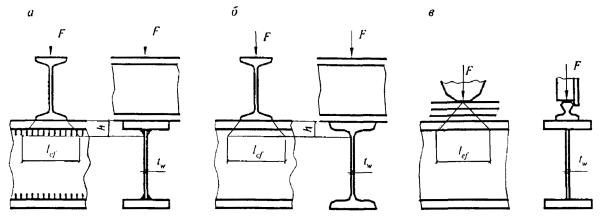
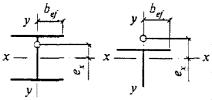
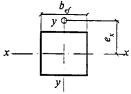
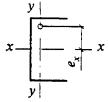
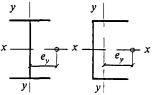
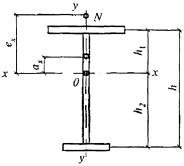
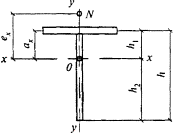
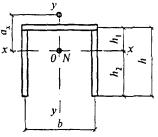
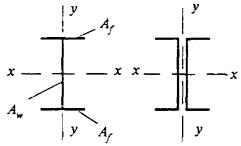
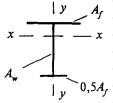
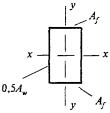
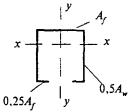
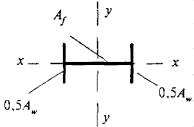
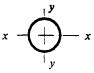
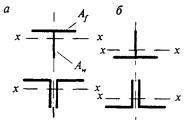
8.3.1 При проверке устойчивости стенок в качестве расчетной высоты hef принимают (рисунок 5):
полную высоту стенки - в сварных элементах;
расстояние между ближайшими к оси элемента краями поясных уголков - в элементах с фрикционными поясными соединениями;
расстояние между началами внутренних закруглений - в прокатных профилях;
расстояние между краями выкружек - в гнутых профилях.
Рисунок 5 - Расчетные размеры стенок, свесов полок, поясных листов в прокатных, составных и гнутых профилях
8.3.2 Устойчивость стенок центрально-сжатых элементов сплошного
сечения, как правило, считают обеспеченной, если условная гибкость стенки ![]() не превышает значений предельной
условной гибкости
не превышает значений предельной
условной гибкости ![]() , определяемых по формулам таблицы 8 и принимаемых не более значений, указанных в правой части
неравенств.
, определяемых по формулам таблицы 8 и принимаемых не более значений, указанных в правой части
неравенств.
8.3.3 Стенки центрально-сжатых элементов сплошного сечения (колонн,
стоек, опор и т.п.) при ![]() , как правило, укрепляют поперечными ребрами жесткости с
шагом от 2,5hef до 3hef; на каждом отправочном элементе должно
быть не менее двух ребер.
, как правило, укрепляют поперечными ребрами жесткости с
шагом от 2,5hef до 3hef; на каждом отправочном элементе должно
быть не менее двух ребер.
В сплошностенчатых ветвях колонн сквозного сечения ребра жесткости допускается устанавливать только в узлах крепления соединительных решеток (планок).
В стенке, укрепленной только поперечными ребрами, ширина их
выступающей части br должна быть для парного симметричного ребра не менее (hef/30 + 40) мм, для одностороннего ребра - не менее (hef/20 + 50) мм; толщина ребра tr должна быть не менее ![]() .
.
Таблица 8
|
Условная
гибкость элемента |
Предельная
условная гибкость стенки |
|
|
|
≤ 2 |
1,30 + 0,15 |
|
> 2 |
1,20 + 0,35 |
|
|
|
≤ 1 |
1,2 (25) |
|
> 1 |
1,0 + 0,2 |
|
|
|
≤ 0,8 |
1,0 (27) |
|
> 0,8 |
0,85 + 0,19 |
|
|
|
0,8 ≤ |
(0,40 + 0,07
|
|
Обозначения, принятые в таблице 8:
bf - ширина полки тавра. Примечания 1 В
коробчатом сечении значение 2 В
тавровом сечении должно соблюдаться условие 1
≤ bf/hef ≤ 2; при 3
Знак «≤» в формулах означает, что
значение |
||
Стенки допускается укреплять односторонними поперечными ребрами жесткости из одиночных уголков, приваренных к стенке пером. Момент инерции такого ребра, вычисляемый относительно оси, совпадающей с ближайшей к ребру гранью стенки, должен быть не менее чем для парного симметричного ребра.
8.3.4 В центрально-сжатых элементах двутаврового сечения с расчетной
высотой стенки hef в случае ее укрепления продольным ребром жесткости, расположенным
посередине и имеющим момент инерции сечения Irl, при ![]() следует значение
следует значение ![]() , установленное
в 8.3.2, умножить на коэффициент
, установленное
в 8.3.2, умножить на коэффициент
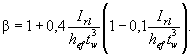 (30)
(30)
При расположении ребра с одной стороны стенки его момент инерции вычисляют относительно оси, совпадающей с ближайшей гранью стенки.
В случае выполнения продольного ребра в виде гофра стенки при вычислении hef учитывают развернутую длину гофра.
Продольные ребра жесткости включают в расчетные сечения элементов.
Минимальные размеры выступающей части продольных ребер жесткости принимают как для поперечных ребер согласно требованиям 8.3.3.
8.3.5 В случаях когда
фактическое значение условной гибкости стенки ![]() превышает предельное
значение
превышает предельное
значение ![]() , вычисленное
по формулам (23) - (28) таблицы 8, проверку устойчивости элемента по формуле (7)
допускается выполнять с учетом расчетной уменьшенной площади сечения Ad согласно приложению Т.
, вычисленное
по формулам (23) - (28) таблицы 8, проверку устойчивости элемента по формуле (7)
допускается выполнять с учетом расчетной уменьшенной площади сечения Ad согласно приложению Т.
8.3.6 При проверке устойчивости поясных листов в качестве расчетной ширины свеса bef принимают расстояние:
от грани стенки до края поясного листа (полки) - в сварных элементах;
от оси крайнего болта в поясе до края поясного листа - в элементах с фрикционными поясными соединениями;
от начала внутреннего закругления до края полки - в прокатных профилях;
от края выкружки до края полки - в гнутых профилях (рисунок 5).
8.3.7 Устойчивость поясных листов и полок центрально-сжатых элементов
сплошного сечения считают обеспеченной, если условная гибкость свеса пояса
(полки) ![]() не превышает значений
предельной условной гибкости свеса пояса (полки)
не превышает значений
предельной условной гибкости свеса пояса (полки) ![]() , определяемых по формулам таблицы 9, в которых при значениях
, определяемых по формулам таблицы 9, в которых при значениях ![]() <
0,8 или
<
0,8 или ![]() > 4 принимают
соответственно
> 4 принимают
соответственно ![]() = 0,8 или
= 0,8 или ![]() = 4.
= 4.
Таблица 9
|
Предельная
условная гибкость свеса пояса (полки) |
|
|
|
0,36 + 0,10 |
|
|
0,43 + 0,08 |
|
|
0,40 + 0,07 |
|
|
0,85 + 0,19 |
|
Обозначение, принятое в таблице 9:
Примечание
- Для свесов пояса
(полок), окаймленных ребрами (рисунок 5), предельные значения условной гибкости |
|
8.3.8 В центрально-сжатых элементах
коробчатого сечения предельную условную гибкость поясного листа ![]() принимают по таблице 8 как для стенок коробчатого сечения:
принимают по таблице 8 как для стенок коробчатого сечения: ![]()
8.3.9 Высота окаймляющего ребра свеса пояса (полки) aef
(рисунок 5), измеряемая от его оси, должна быть не менее 0,3bef в элементах,
не усиленных планками, и 0,2bef
- в элементах,
усиленных планками (таблица 9); при этом толщина ребра должна быть не менее ![]()
8.3.10 При назначении сечений
центрально-сжатых элементов по предельной гибкости значения предельных условных гибкостей стенки и поясов ![]() , определяемых соответственно по
таблицам 8
и 9, допускается увеличивать
умножением на коэффициент
, определяемых соответственно по
таблицам 8
и 9, допускается увеличивать
умножением на коэффициент ![]() , но не более
чем в 1,25
раза.
, но не более
чем в 1,25
раза.
9 РАСЧЕТ ЭЛЕМЕНТОВ СТАЛЬНЫХ КОНСТРУКЦИЙ ПРИ ИЗГИБЕ
9.1 ОБЩИЕ ПОЛОЖЕНИЯ РАСЧЕТА
В зависимости от назначения, условий эксплуатации расчет изгибаемых элементов (балок) выполняют без учета или с учетом пластических деформаций в соответствии с подразделением элементов на три класса согласно 5.2.6.
Балки 1-го класса применяют для всех видов нагрузок и рассчитывают в пределах упругих деформаций; балки 2-го и 3-го классов применяют для статических нагрузок и рассчитывают с учетом развития пластических деформаций.
Балки крановых путей (из однородной стали и бистальные) под краны групп режимов работы 1К - 5К по ГОСТ 25546 при расчете на прочность допускается относить ко 2-му классу, при остальных расчетах - следует относить к 1-му классу.
Другие бистальные балки относят ко 2-му классу и рассчитывают с учетом ограниченных пластических деформаций в стенке, значения которых должны определяться достижением расчетного сопротивления Ryf в поясах, выполненных из более прочной стали.
9.2 РАСЧЕТ НА ПРОЧНОСТЬ ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ СПЛОШНОГО СЕЧЕНИЯ
9.2.1 Расчет на прочность балок 1-го класса выполняют по формулам:
при действии момента в одной из главных плоскостей
при действии в сечении поперечной силы
при действии моментов в двух главных плоскостях
где х и у - расстояния от главных осей до рассматриваемой точки сечения;
при одновременном действии в стенке балки момента и поперечной силы
где σx = Myy/Iхп - нормальное напряжение в срединной плоскости стенки, параллельное продольной оси балки;
σy - то же, перпендикулярное продольной оси балки, в том числе σloc, определяемое по формуле (41);
τxy = QS/(Itw) - касательное напряжение в стенке.
Напряжения σx и σy, принимаемые в формуле (38) со своими знаками, а также τxy определяют в одной и той же точке стенки балки.
При ослаблении стенки отверстиями для болтов левую часть формулы (36), а также значение τxy в формуле (38) умножают на коэффициент
где s - шаг отверстий;
d - диаметр отверстия.
В балках, рассчитываемых по формуле (37), значения напряжений в стенке балки должны быть проверены по формуле (38) в двух главных плоскостях изгиба.
9.2.2 Расчет на прочность стенки балки, не укрепленной ребрами жесткости, при действии местного напряжения σloc в местах приложения нагрузки к поясу, а также в опорных сечениях балки выполняют по формуле
![]() (40)
(40)
где σloc = F/(leftw). (41)
а - сварной; б - прокатной; в - сварной или прокатной при нагрузке от колеса крана
Рисунок 6 - Схемы распределения сосредоточенной нагрузки на стену балки
Здесь F - расчетная нагрузка (сила), принимаемая согласно СНиП 2.01.07;
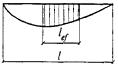
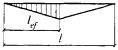
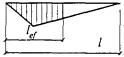
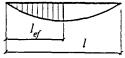
lef - условная длина распределения нагрузки, определяемая по формулам:
для случаев по рисункам 6, а и 6, б
lef = b + 2h; (42)
для случая по рисунку 6, в
![]() (43)
(43)
где h - размер, равный сумме толщины верхнего пояса балки и катета поясного шва, если нижняя балка сварная (рисунок 6, а), либо расстоянию от наружной грани полки до начала внутреннего закругления стенки, если нижняя балка прокатная (рисунок 6, б);
ψ - коэффициент, принимаемый равным: 3,25 - для сварных и прокатных балок; 4,5 - для балок с фрикционными поясными соединениями;
I1f - сумма собственных моментов инерции пояса балки и кранового рельса или момент инерции сечения, состоящего из пояса и рельса в случае приварки рельса швами, обеспечивающими совместную работу пояса и рельса.
9.2.3 Расчет на прочность разрезных балок 2-го и 3-го классов двутаврового и коробчатого сечений (рисунок 7) из стали с нормативным сопротивлением Ry ≤ 440 Н/мм2 при соблюдении требований 9.4.6, 9.5.8, 9.5.9 и 9.5.14 и при касательных напряжениях τx = Qx/Aw ≤ 0,9Rs (кроме опорных сечений) выполняют по формулам:
при изгибе в плоскости наибольшей жесткости (Ix > Iy)
при изгибе в двух главных плоскостях и напряжениях τy = Qy/(2Af) ≤ 0,5Rs
Здесь Mx, My - абсолютные значения изгибающих моментов;
cx, cy - коэффициенты, принимаемые согласно таблице К.1 приложения К;
β - коэффициент, принимаемый равным:
при τ ≤ 0,5Rs β = 1;
при 0,5Rs < τx ≤ 0,9Rs
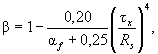 (46)
(46)
где αf = Af/Aw - отношение площадей пояса и стенки (для несимметричного сечения Af - площадь меньшего пояса; для коробчатого сечения Aw - суммарная площадь двух стенок).
Рисунок 7 - Схемы двутаврового (а) и коробчатого (б) сечений и действующие усилия
При расчете сечения в зоне чистого изгиба в формулах (44) и (45) принимают β = 1 и вместо коэффициентов cx и cy соответственно
cxm = 0,5(1 + cx); cym = 0,5(1 + cy). (47)
Расчет на прочность в опорном сечении балок (при Mx = 0 и My = 0) выполняют по формуле
При ослаблении стенки отверстиями для болтов левую часть формулы (48), а также значения касательных напряжений τ умножают на коэффициент α, определяемый по формуле (39).
С целью установления размеров минимальных сечений составных балок значения коэффициентов cx и cy допускается принимать меньше значений, приведенных в приложении К. Методика подбора минимальных сечений изгибаемых элементов приведена в приложении Л.
9.2.4 При расчете на прочность разрезных балок переменного сечения согласно 9.2.3 учет пластических деформаций допускается только в одном сечении; в остальных сечениях балки расчет выполняют при значениях коэффициентов cx и cy, меньших, чем приведенные в таблице К.1 обязательного приложения К, или согласно 9.2.1.
9.2.5 Расчет на прочность неразрезных и защемленных балок постоянного двутаврового и коробчатого сечений с двумя осями симметрии, изгибаемых в плоскости наибольшей жесткости, со смежными пролетами, отличающимися не более чем на 20 %, при соблюдении требований 9.4.6, 9.5.8, 9.5.9 и 9.5.14 выполняют по формуле (44) как сечений 2-го класса с учетом частичного перераспределения опорных и пролетных моментов.
Расчетное значение момента определяют по формуле
M = 0,5(Mmax + Mef), (49)
где Mmax - наибольший изгибающий момент в пролете или на опоре, определяемый из расчета неразрезной балки в предположении упругой работы стали;
Mef - условный изгибающий момент, равный:
а) в неразрезных балках со свободно опертыми концами большему из значений:
Mef = 0,5M2, (51)
где символ max означает, что следует найти максимум всего следующего за ним выражения;
M1 - изгибающий момент в крайнем пролете, вычисленный как в свободно опертой однопролетной балке;
a - расстояние от сечения, в котором действует момент M1, до крайней опоры;
l - длина крайнего пролета;
M2 - максимальный изгибающий момент в промежуточном пролете, вычисленный как в свободно опертой однопролетной балке;
б) в однопролетных и неразрезных балках с защемленными концами Mef = 0,5M3, где M3 - наибольший из моментов, вычисленных как в балках с шарнирами на опорах;
в) в балке с одним защемленным и другим свободно опертым концом значение Me следует определять по формуле (50).
Значение τx в формуле (46) вычисляют в сечении, где действует Mmax; если Mmax - момент в пролете, то проверяют опорное сечение балки.
9.2.6 Расчет на прочность неразрезных и защемленных балок, удовлетворяющих требованиям 9.2.5, в случае изгиба в двух главных плоскостях выполняют по формуле (45) с учетом частичного перераспределения опорных и пролетных моментов в двух главных плоскостях согласно требованиям 9.2.5.
9.2.7 Расчет на прочность неразрезных и защемленных балок, удовлетворяющих требованиям 9.2.5, 9.4.6, 9.5.8, 9.5.9 и 9.5.14, допускается выполнять по формуле (44) как сечений 3-го класса с учетом полного перераспределения изгибающих моментов и образования пластических шарниров, а также влияния касательных напряжений τx (по формуле (46)) в сечениях с максимальным изгибающим моментом.
9.2.8 Расчет на прочность бистальных разрезных балок двутаврового и коробчатого сечений с двумя осями симметрии при соблюдении требований 9.4.4, 9.5.9 и 9.5.13 и при касательных напряжениях τx ≤ 0,9Rs, τy ≤ 0,5Rs (кроме опорных сечений) выполняют как расчет сечений 2-го класса по формулам:
при изгибе в одной главной плоскости
при изгибе в двух главных плоскостях
В формулах (52) и (53) обозначено:
cxr = (αfr + 0,25 - 0,0833/r2)/(αf + 0,167) (54)
(где αf = Af/Aw, r = Ryf/Ryw);
βr - коэффициент, принимаемый равным:
при τx ≤ 0,5Rs βr = 1;
при 0,5Rs < τx < 0,9Rs
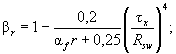 (55)
(55)
cyr - коэффициент, принимаемый равным 1,15 - для двутаврового сечения и 1,05/r - для коробчатого сечения.
Расчет бистальных балок при наличии зоны чистого изгиба и в опорном сечении, а также с учетом ослабления сечения выполняют согласно 9.2.3.
9.3 РАСЧЕТ НА ПРОЧНОСТЬ БАЛОК КРАНОВЫХ ПУТЕЙ СПЛОШНОГО СЕЧЕНИЯ
9.3.1 Расчет на прочность балок крановых путей выполняют согласно требованиям 9.2.1 на действие вертикальных и горизонтальных нагрузок, определяемых согласно СНиП 2.01.07.
При расчете балок крановых путей двутаврового сечения для кранов групп режимов работы 1К - 5К допускается учитывать ограниченные пластические деформации путем умножения величин Wn,min и Ixn в формулах (35) и (37) на коэффициент 1,05 при αf ≤ 1 и величины Iyn в формуле (37) - на 1,15.
9.3.2 Расчет на прочность стенок балок крановых путей (за исключением балок, рассчитываемых на усталость, для кранов групп режимов работы 7К в цехах металлургических производств и 8К) выполняют по формуле (38), в которой при расчете сечений на опорах неразрезных балок вместо коэффициента 0,87 принимают коэффициент 0,77.
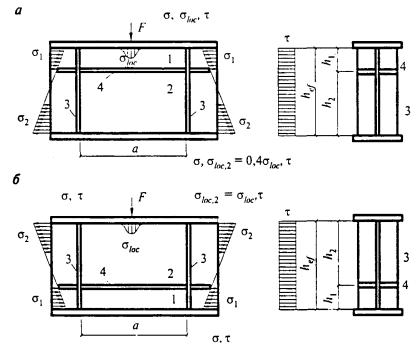
9.3.3 Расчет на прочность стенок балок крановых путей, рассчитываемых на усталость, для кранов групп режимов работы 7К (в цехах металлургических производств) и 8К из стали с пределом текучести не более 440 Н/мм2 выполняют по формулам:
(1/Ry)(σx + σloc,x) ≤ 1; (57)
(1/Ry)(σloc,y + σfy) ≤ 1; (58)
(1/Rs)(τxy + τloc,xy + τf,xy) ≤ 1, (59)
где β - коэффициент, принимаемый равным 0,87 для расчета разрезных балок и 0,77 - для расчета сечений на опорах неразрезных балок;
σx = M/Wxn; σloc,x = 0,25σloc,y;
σloc,y = γfγf1Fn/(tlef); σfy = 2Mtt/If; (60)
τxy = Q/(th); τloc,xy = 0,3σloc,y; τfxy = 0,25σfy.
В формулах (60) обозначено:
M и Q - соответственно изгибающий момент и поперечная сила в сечении балки от расчетной нагрузки, определяемой согласно СНиП 2.01.07;
γf - коэффициент надежности по нагрузке для крановых нагрузок, принимаемый согласно СНиП 2.01.07;
γf1 - коэффициент увеличения сосредоточенной вертикальной нагрузки от одного колеса крана, принимаемый согласно СНиП 2.01.07;
Fn - полное нормативное значение сосредоточенной вертикальной нагрузки от одного колеса крана;
lef - условная длина, определяемая согласно требованиям 9.2.2;
Mt - местный крутящий момент, определяемый по формуле
Mt = γfγf1Fne + 0,75Qthr, (61)
где e - условный эксцентриситет, принимаемый равным 15 мм;
Qt - расчетная горизонтальная нагрузка, направленная поперек кранового пути, вызываемая перекосами мостовых кранов и непараллельностью крановых путей и принимаемая согласно СНиП 2.01.07;
hr - высота кранового рельса;
If = It + bftf3/3 - сумма моментов инерции при кручении рельса и пояса (bf и tf - ширина и толщина верхнего пояса балки).
Все напряжения в формулах (56) - (60) принимают со знаком «плюс».
9.3.4 Расчет на прочность подвесных балок крановых путей (монорельсов) выполняют с учетом местных нормальных напряжений от давления колеса крана, направленных вдоль и поперек оси балки.
9.3.5 Расчет на прочность бистальных балок крановых путей двутаврового сечения с двумя осями симметрии для кранов групп режимов работы 1К - 5К при r = Ryf/Ryw ≤ 1,5 допускается выполнять по формуле (53), в которой принимают:
My - изгибающий момент в горизонтальной плоскости, полностью передающийся на верхний пояс балки;
Wxn = Wxnf - момент сопротивления сечения верхнего пояса относительно оси y-y;
cyr - коэффициент, принимаемый равным 1,15.
Расчет на прочность стенок бистальных балок крановых путей выполняют согласно требованиям 9.3.2.
9.4 РАСЧЕТ НА УСТОЙЧИВОСТЬ ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ СПЛОШНОГО СЕЧЕНИЯ
9.4.1 Расчет на устойчивость двутавровых балок 1-го класса, а также бистальных балок 2-го класса при выполнении требований 9.2.1 и 9.2.8 выполняют по формулам:
при изгибе в плоскости стенки, совпадающей с плоскостью симметрии сечения
при изгибе в двух главных плоскостях
В формулах (62) и (63) обозначено:
φb - коэффициент устойчивости при изгибе, определяемый по обязательному приложению М для балок с опорными сечениями, закрепленными от боковых смещений и поворота;
Wcx - момент сопротивления сечения относительно оси x-x, вычисленный для сжатого пояса;
Wy - момент сопротивления сечения относительно оси y-y, совпадающей с плоскостью изгиба.
Для бистальных балок в формулах (62) и (63), а также при определении φb заменяют Ry на Ryf.
9.4.2 При определении значения φb за расчетную длину балки lef принимают расстояние между точками закреплений сжатого пояса от поперечных смещений (узлами продольных или поперечных связей, точками крепления жесткого настила); при отсутствии связей lef = l (где l - пролет балки); за расчетную длину консоли принимают lef = l при отсутствии закрепления сжатого пояса на конце консоли в горизонтальной плоскости (здесь l - длина консоли) и расстояние между точками закрепления сжатого пояса в горизонтальной плоскости при закреплении пояса на конце и по длине консоли.
9.4.3 Расчет на устойчивость балок крановых путей двутаврового сечения выполняют по формуле (63), в которой необходимо принять: My - изгибающий момент в горизонтальной плоскости, полностью передающийся на верхний пояс балки; Wy = Wyf - момент сопротивления сечения верхнего пояса относительно оси y-y.
9.4.4 Устойчивость балок 1-го класса, а также бистальных балок 2-го класса считают обеспеченной:
а) при передаче нагрузки на балку через сплошной жесткий настил (плиты железобетонные из тяжелого, легкого и ячеистого бетона, плоский и профилированный металлический настил, волнистая сталь и т.п.), непрерывно опирающийся на сжатый пояс балки и с ним связанный с применением сварки, болтов, самонарезающих винтов и др.; при этом силы трения учитывать не следует;
б) при значениях условной гибкости сжатого пояса балки ![]() , не
превышающих ее предельных значений
, не
превышающих ее предельных значений ![]() , определяемых по формулам таблицы
10 для балок симметричного
двутаврового сечения и асимметричного с более развитым сжатым поясом,
рассчитываемых по формуле (62) и
имеющих отношение ширины растянутого пояса к ширине сжатого пояса не менее 0,75.
, определяемых по формулам таблицы
10 для балок симметричного
двутаврового сечения и асимметричного с более развитым сжатым поясом,
рассчитываемых по формуле (62) и
имеющих отношение ширины растянутого пояса к ширине сжатого пояса не менее 0,75.
9.4.5 Прикрепления к сжатому поясу жесткого настила, продольных или поперечных связей, которые должны обеспечить устойчивость изгибаемого элемента, рассчитывают на фактическую или условную поперечную силу; при этом условную поперечную силу определяют:
при закреплении балки в отдельных точках - по формуле (18), в которой φ определяют по кривой устойчивости b при гибкости λ = lef/i (где i - радиус инерции сечения сжатого пояса в горизонтальной плоскости), а N - вычисляют по формуле
N = (Afr + 0,25Aw)Ryw, (67)
где Af и Aw - площади сечения сжатого пояса и стенки соответственно;
r = Ryf/Ryw ≥ 1,0;
Ryf и Ryw - расчетные сопротивления стали сжатого пояса и стенки соответственно;
при непрерывном закреплении - по формуле
qfic = 3Qfic/l, (68)
где qfic - условная поперечная сила на единицу длины пояса балки;
Qfic - условная поперечная сила, определяемая по формуле (18), в которой принимают φ = 1, а N определяют по формуле (67).
Таблица 10
|
Место приложения нагрузки |
Условная
предельная гибкость сжатого пояса прокатной
или сварной
балки |
|
К верхнему поясу |
|
|
К нижнему поясу |
0,57 + 0,0032b/t + (0,92 - 0,02b/t)b/h (65) |
|
Независимо от уровня приложения нагрузки при расчете участка балки между связями или при чистом изгибе |
0,41 + 0,0032b/t + (0,73 - 0,016b/t)b/h (66) |
|
Обозначения, принятые в таблице 10: b и t - ширина и толщина сжатого пояса соответственно; h - расстояние (высота) между осями поясных листов. Примечания 1
Значения 2 Для
балок с фрикционными поясными соединениями значения 3
Значения |
|
9.4.6 Устойчивость балок с сечениями 2-го и 3-го классов считают обеспеченной при выполнении требований 9.4.4а либо 9.4.4б при условии умножения значений ![]() , определяемых по формулам
таблицы 10, на коэффициент
, определяемых по формулам
таблицы 10, на коэффициент
δ = 1 - 0,6(c1x - 1)/(c - 1), (69)
где c1x - коэффициент, определяемый по формулам:
c1x = Mx/(WxnRyγc) или c1x = βcx (70)
и изменяющийся в пределах 1 < c1x< cx.
Здесь Mx - изгибающий момент в сечении;
β - коэффициент, принимаемый по формуле (46);
cx - коэффициент, принимаемый согласно таблице К.1 приложения К.
При этом допускается принимать значения условной предельной гибкости пояса балки:
δ![]() - на участке длины балки, где учитываются
пластические деформации;
- на участке длины балки, где учитываются
пластические деформации;
![]() - на участках длины балки с
напряжениями в сечениях σ = M/Wn,min ≤ Ryγc.
- на участках длины балки с
напряжениями в сечениях σ = M/Wn,min ≤ Ryγc.
Учет пластических деформаций при расчете балок со сжатым поясом, менее развитым, чем растянутый, допускается лишь при выполнении требований 9.4.4а.
9.5 ПРОВЕРКА УСТОЙЧИВОСТИ СТЕНОК И ПОЯСНЫХ ЛИСТОВ ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ СПЛОШНОГО СЕЧЕНИЯ
9.5.1 Устойчивость стенок балок 1-го класса считают обеспеченной, если выполнены требования 9.2.1, 9.3.1 - 9.3.3,
9.4.1 - 9.4.5 и
условная гибкость стенки ![]() (рисунок 5) не превышает значений:
(рисунок 5) не превышает значений:
3,5 - при отсутствии местного напряжения в балках с двусторонними поясными швами;
3,2 - то же, в балках с односторонними поясными швами;
2,5 - при действии местного напряжения в балках с двусторонними поясными швами.
При этом устанавливают поперечные (и опорные) ребра жесткости согласно требованиям 9.5.9, 9.5.11 и 9.5.12 настоящего Свода правил.
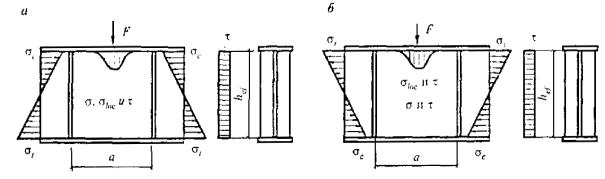
9.5.2 Проверку устойчивости стенок балок 1-го класса выполняют с учетом наибольшего сжимающего напряжения σ у расчетной границы стенки, принимаемого со знаком «плюс», среднего касательного напряжения τ и местного напряжения в стенке σloc под сосредоточенной нагрузкой.
Напряжения σ и τ вычисляют по формулам:
σ = My/Ix; (71)
τ = Q/(twhw), (72)
где M и Q - средние значения изгибающего момента и поперечной силы соответственно в пределах отсека; если длина отсека a больше его расчетной высоты hef, то значения M и Q вычисляют как средние для более напряженного участка с длиной, равной hef; если в пределах отсека момент или поперечная сила меняют знак, то их средние значения вычисляют на участке отсека с одним знаком усилия M или Q (здесь a - расстояние между осями поперечных ребер жесткости);
hef - расчетная высота стенки, принимаемая согласно требованиям 8.3.1;
hw - полная высота стенки.
Местное напряжение σloc (σloc,y) в стенке под сосредоточенной нагрузкой определяют согласно 9.2.2 и 9.3.3.
В отсеках балки, где сосредоточенная нагрузка приложена к растянутому поясу, одновременно учитывают только σ и τ или σloc и τ.
9.5.3 Устойчивость стенок балок 1-го класса
симметричного сечения, укрепленных только поперечными ребрами жесткости, при
условной гибкости стенки ![]() считают обеспеченной,
если выполнено условие
считают обеспеченной,
если выполнено условие
В формуле (73) обозначено:
σ, σloc, τ - напряжения, определяемые согласно требованиям 9.5.2;
σcr - критическое напряжение, вычисляемое по формуле
σcr = ccrRy/![]() (74)
(74)
где ccr - коэффициент, определяемый согласно 9.5.4 - 9.5.6;
σloc,cr - критическое напряжение, вычисляемое по формуле
σloc,cr = c1c2Ry/![]() (75)
(75)
где c1 и c2 - коэффициенты определяемые согласно 9.5.5;
τcr - критическое напряжение, вычисляемое по формуле
τcr
= 10,3(1
+ 0,76/μ2)Rs/![]() (76)
(76)
здесь μ - отношение большей стороны отсека стенки к меньшей;
![]()
d - меньшая из сторон отсека стенки (hef или a).
9.5.4 Для балок по 9.5.3 при σloc = 0 коэффициент ccr в формуле (74) определяют по таблице 11 в зависимости от вида поясных соединений и значения коэффициента δ, вычисляемого по формуле
где β - коэффициент, принимаемый по таблице 12;
bf, tf - ширина и толщина сжатого пояса балки.
Таблица 11
|
Значение ccr при δ, равном |
|||||||
|
≤ 0,8 |
1,0 |
2,0 |
4,0 |
6,0 |
10,0 |
≥ 30,0 |
|
|
Сварные |
30,0 |
31,5 |
33,3 |
34,6 |
34,8 |
35,1 |
35,5 |
|
Фрикционные |
35,2 |
||||||
Таблица 12
|
Условия работы сжатого пояса |
β |
|
|
Крановых путей |
Крановые рельсы не приварены |
2,0 |
|
Крановые рельсы приварены |
∞ |
|
|
Прочие |
При непрерывном опирании плит |
∞ |
|
В прочих случаях |
0,8 |
|
|
Примечание - Для отсеков балок крановых путей, где сосредоточенная нагрузка приложена к растянутому поясу, следует принимать β = 0,8. |
||
а - при приложении сосредоточенной нагрузки к сжатому поясу; б - то же, к растянутому поясу
Рисунок 8 - Схема участка балки, укрепленной поперечными ребрами жесткости
9.5.5 Для балок по 9.5.3 при σloc ≠ 0 (рисунок 8) значение σloc,cr определяют по формуле (75),
где c1 - коэффициент, принимаемый по таблице 13 в зависимости от отношения a/hef и значения ρ = 1,04lef/hef (здесь значение lef следует определять согласно требованиям 9.2.2);
c2 - коэффициент, принимаемый по таблице 14 в зависимости от отношения a/hef и значения δ, вычисляемого по формуле (77); для балок с фрикционными поясными соединениями принимают δ = 10.
Таблица 13
|
Значения коэффициента c1 при a/hef (a1/hef), равном |
||||||||||
|
0,50 |
0,60 |
0,67 |
0,80 |
1,0 |
1,2 |
1,4 |
1,6 |
1,8 |
≥ 2,0 |
|
|
0,10 |
56,7 |
46,6 |
41,8 |
34,9 |
28,5 |
24,5 |
21,7 |
19,5 |
17,7 |
16,2 |
|
0,15 |
38,9 |
31,3 |
27,9 |
23,0 |
18,6 |
16,2 |
14,6 |
13,6 |
12,7 |
12,0 |
|
0,20 |
33,9 |
26,7 |
23,5 |
19,2 |
15,4 |
13,3 |
12,1 |
11,3 |
10,7 |
10,2 |
|
0,25 |
30,6 |
24,9 |
20,3 |
16,2 |
12,9 |
11,1 |
10,0 |
9,4 |
9,0 |
8,7 |
|
0,30 |
28,9 |
21,6 |
18,5 |
14,5 |
11,3 |
9,6 |
8,7 |
8,1 |
7,8 |
7,6 |
|
0,35 |
28,0 |
20,6 |
17,4 |
13,4 |
10,2 |
8,6 |
7,7 |
7,2 |
6,9 |
6,7 |
|
0,40 |
27,4 |
20,0 |
16,8 |
12,7 |
9,5 |
7,9 |
7,0 |
6,6 |
6,3 |
6,1 |
Таблица 14
|
Значения коэффициента c2 при a/hef (a1/hef), равном |
||||||||
|
0,50 |
0,60 |
0,67 |
0,80 |
1,00 |
1,20 |
1,40 |
≥ 1,60 |
|
|
≤ 1 |
1,56 |
1,56 |
1,56 |
1,56 |
1,56 |
1,56 |
1,56 |
1,56 |
|
2 |
1,64 |
1,64 |
1,64 |
1,67 |
1,76 |
1,82 |
1,84 |
1,85 |
|
4 |
1,66 |
1,67 |
1,69 |
1,75 |
1,88 |
2,01 |
2,09 |
2,12 |
|
6 |
1,67 |
1,68 |
1,70 |
1,77 |
1,92 |
2,08 |
2,19 |
2,26 |
|
10 |
1,68 |
1,69 |
1,71 |
1,78 |
1,96 |
2,14 |
2,28 |
2,38 |
|
≥ 30 |
1,68 |
1,70 |
1,72 |
1,80 |
1,99 |
2,20 |
2,38 |
2,52 |
При σloc ≠ 0 проверку стенки по формуле (73) следует выполнять в зависимости от значения a/hef:
а) при отношении a/hef ≤ 0,8 значение ccr определяют по формуле (74) с учетом требований 9.5.4.
Если сосредоточенная нагрузка приложена к растянутому поясу, то при проверке стенки с учетом только σloc и τ (рисунок 8, б) при определении коэффициента δ по формуле (77) значения bf и tf принимают для растянутого пояса;
б) при отношении a/hef > 0,8 проверку по формуле (73) выполняют дважды:
при значении σcr, вычисленном по формуле (74) с учетом требований 9.5.4, и при таком значении σloc,cr, для вычисления которого по формуле (75) при определении коэффициентов c1 и c2 вместо размера a необходимо принять a1 = 0,5a при 0,8 ≤ a/hef ≤ 1,33 и a1 = 0,67hef при a/hef > 1,33;
при значениях σcr и σloc,cr, вычисленных при фактическом значении a/hef (если a/hef > 2, в расчете принимают a/hef = 2); при этом коэффициент ccr в формуле (74) определяют по таблице 15.
Таблица 15
|
Значения ccr при a/hef или a/(2hc), равном |
|||||||
|
≤ 0,8 |
0,9 |
1,0 |
1,2 |
1,4 |
1,6 |
1,8 |
≥ 2,0 |
|
По таблице 11 |
37,0 |
39,2 |
45,2 |
52,8 |
62,0 |
72,6 |
84,7 |
Значение τcr во всех случаях вычисляют по фактическим размерам отсека.
9.5.6 Устойчивость стенок балок 1-го класса асимметричного двутаврового сечения с более развитым сжатым поясом, укрепленных только поперечными ребрами жесткости, считают обеспеченной, если условие (73) будет выполнено с учетом следующих изменений:
при определении значений σcr в формулах (74) и (77) вместо значения hef принимают удвоенную высоту сжатой зоны стенки 2hc;
при a/(2hc) > 0,8 и σloc ≠ 0 следует выполнять две проверки, указанные в 9.5.5, принимая hef = 2hc при определении ccr по таблице 15 и σcr - по формуле (74).
Значения τcr и σloc,cr определяют по фактическим размерам отсека стенки.
9.5.7 Устойчивость стенок балок 1-го класса асимметричного двутаврового сечения с более развитым растянутым поясом, укрепленных только поперечными ребрами жесткости, при одновременном действии напряжений σ и τ и отсутствии напряжений σloc считают обеспеченной, если выполнено условие
![]() (78)
(78)
где α = (σ1 - σ2)/σ1; β = (σcr/σ1)(τ/τcr); σcr = (ccrRy)/![]() .
.
Здесь σ1 и σ2 - сжимающее и растягивающее напряжения у расчетных границ стенки, принимаемые соответственно со знаком «плюс» и «минус» и определяемые по формуле (71);
τ и τcr - касательные напряжения, определяемые соответственно по формулам (72) и (76);
ccr - коэффициент, определяемый по таблице 16 в зависимости от α.
Таблица 16
|
1,0 |
1,2 |
1,4 |
1,6 |
1,8 |
2,0 |
|
|
ccr |
10,2 |
12,7 |
15,5 |
20,0 |
25,0 |
30,0 |
9.5.8 Устойчивость стенок балок 2-го и 3-го классов из однородной стали и бистальных при отсутствии местного напряжения (σloc = 0) и с соблюдением требований 8.3.1, 9.2.3 и 9.2.8 считают обеспеченной при выполнении условий:
а) для двоякосимметричного двутаврового и коробчатого сечений
M/[Ryfγchef2t(rαf + α)] ≤ 1, (79)
где α определяют по данным таблицы 17 (значение τ принимают равным τ = Q/Aw);
Таблица 17
|
τ/Rsw |
Значения
α при |
|||||||
|
2,2 |
2,5 |
3,0 |
3,5 |
4,0 |
4,5 |
5,0 |
5,5 |
|
|
0 |
0,240 |
0,239 |
0,235 |
0,226 |
0,213 |
0,195 |
0,173 |
0,153 |
|
0,5 |
0,203 |
0,202 |
0,197 |
0,189 |
0,176 |
0,158 |
0,136 |
0,116 |
|
0,6 |
0,186 |
0,185 |
0,181 |
0,172 |
0,159 |
0,141 |
0,119 |
0,099 |
|
0,7 |
0,167 |
0,166 |
0,162 |
0,152 |
0,140 |
0,122 |
0,100 |
0,080 |
|
0,8 |
0,144 |
0,143 |
0,139 |
0,130 |
0,117 |
0,099 |
0,077 |
0,057 |
|
0,9 |
0,119 |
0,118 |
0,114 |
0,105 |
0,092 |
0,074 |
0,052 |
0,032 |
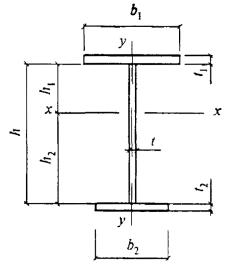
б) для балок асимметричного двутаврового сечения с более развитым сжатым поясом, укрепленных только поперечными ребрами,
M/{[σ1Af1h1 + σ2Af2(hw - h1) + 4h12tαRyw + hwt(hw
- 2h1)![]() ]γc} ≤ 1, (80)
]γc} ≤ 1, (80)
где σ1, σ2 - напряжения в сжатом и растянутом поясах соответственно; если σ1 ≥ Ryf или σ2 ≥ Ryf, то принимают соответственно σ1 = Ryf или σ2 = Ryf.
В выражении (80) высоту сжатой зоны стенки h1 определяют по формуле
h1 = Aw/(2t) + (Af2σ2 - Af1σ1)/(2t![]() ). (81)
). (81)
Значения M и Q определяют в одном сечении балки.
9.5.9 Стенки балок укрепляют поперечными ребрами жесткости:
в балках 1-го класса - если значение
условной гибкости стенки ![]() превышает 3,2 при отсутствии
подвижной нагрузки на поясе балки либо 2,2 - при наличии такой нагрузки;
превышает 3,2 при отсутствии
подвижной нагрузки на поясе балки либо 2,2 - при наличии такой нагрузки;
в балках 2-го и 3-го классов - при любых значениях условной гибкости на участках длины балки, где учитываются пластические деформации, а на остальных участках - как в балках 1-го класса.
Расстояние между поперечными ребрами, как правило, не должно
превышать 2hef при ![]() ≥ 3,2 и 2,5hef - при
≥ 3,2 и 2,5hef - при ![]() < 3,2.
< 3,2.
Для балок 1-го класса
допускается превышать эти расстояния до значения 3hef при условии, что устойчивость
балки и стенки обеспечена выполнением требований 9.4.4а или 9.4.4б, если ![]() не превышает значений, определяемых по
формуле (64).
не превышает значений, определяемых по
формуле (64).
Поперечные ребра жесткости, как правило, устанавливают в местах приложения неподвижных сосредоточенных нагрузок и на опорах балок.
В стенке, укрепленной только поперечными ребрами, ширина их
выступающей части br должна быть для
парного ребра не менее (hw/30 + 25) мм, для
одностороннего - не менее (hw/24 + 40) мм; толщина ребра tr должна быть не менее 2br![]() .
.
При укреплении стенки односторонними поперечными ребрами жесткости из одиночных уголков, привариваемых к стенке пером, момент инерции такого ребра, вычисляемый относительно оси, совпадающей с ближайшей к ребру гранью стенки, должен быть не менее чем для парного ребра.
9.5.10 Поперечное ребро
жесткости, расположенное в месте приложения сосредоточенной нагрузки к верхнему
поясу, проверяют расчетом на устойчивость: двустороннее ребро - как
центрально-сжатую стойку, а одностороннее - как стойку, сжатую с
эксцентриситетом, равным расстоянию от срединной плоскости стенки до центра
тяжести расчетного сечения стойки. При этом в расчетное сечение стойки включают
сечение ребра жесткости и полосы стенки шириной 0,65tw![]() с каждой стороны ребра, а расчетную длину принимают равной высоте
стенки hef.
с каждой стороны ребра, а расчетную длину принимают равной высоте
стенки hef.
9.5.11 Если устойчивость стенок балок 1-го класса
при действии нормальных напряжений σ от изгиба не обеспечена, а
также при значениях условной гибкости стенки ![]() (где σ - напряжение в сжатом
поясе балки) стенки таких балок допускается укреплять продольным ребром
жесткости, устанавливаемым дополнительно к поперечным ребрам согласно
приложению Н, в котором даны требования и для установки промежуточных
поперечных ребер жесткости.
(где σ - напряжение в сжатом
поясе балки) стенки таких балок допускается укреплять продольным ребром
жесткости, устанавливаемым дополнительно к поперечным ребрам согласно
приложению Н, в котором даны требования и для установки промежуточных
поперечных ребер жесткости.
9.5.12 При значениях условной гибкости стенки ![]() балки симметричного
двутаврового сечения допускается проектировать как балки 2-го класса с гибкими (неустойчивыми) стенками согласно
приложению Л.
балки симметричного
двутаврового сечения допускается проектировать как балки 2-го класса с гибкими (неустойчивыми) стенками согласно
приложению Л.
9.5.13 Участок стенки балки над опорой рассчитывают на устойчивость при центральном сжатии из плоскости балки как стойку, нагруженную опорной реакцией.
При укреплении стенки балки опорными ребрами жесткости с шириной
выступающей части br (как правило, не
менее 0,5bfi) в
расчетное сечение этой стойки включают сечение опорных ребер и полосы стенки
шириной не более 0,65tw![]() с каждой стороны ребра (здесь bfi - ширина нижнего пояса балки).
с каждой стороны ребра (здесь bfi - ширина нижнего пояса балки).
Толщина опорного ребра жесткости tr должна быть не менее 3br![]() , где br - ширина выступающей
части.
, где br - ширина выступающей
части.
Расчетную длину стойки принимают равной высоте стенки балки hef.
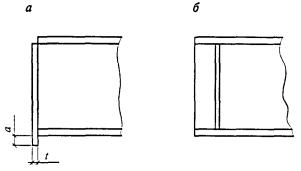
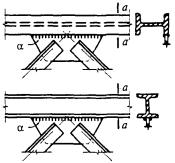
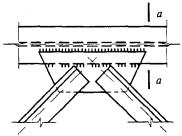
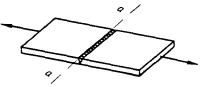
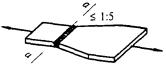
Нижние торцы опорных ребер (рисунок 9) должны быть остроганы либо плотно пригнаны или приварены к нижнему поясу балки. Напряжения в этих сечениях при действии опорной реакции не должны превышать расчетного сопротивления стали: в первом случае (рисунок 9, а) - смятию Rp при a ≤ 1,5t и сжатию Ry при a > 1,5t; во втором случае (рисунок 9, б) - смятию Rp.
Сварные швы, прикрепляющие опорное ребро к нижнему поясу балки, рассчитывают на воздействие опорной реакции.
При отсутствии опорных ребер жесткости (в прокатных балках) сечением стойки является полоса стенки шириной, равной длине участка опирания балки.
а - в торце с применением строжки; б - удаленного от торца с плотной пригонкой или приваркой к нижнему поясу
Рисунок 9 - Схема устройства опорного ребра жесткости
9.5.14 Устойчивость сжатых поясов
считают обеспеченной, если условная гибкость свеса пояса ![]() или поясного листа
или поясного листа ![]() балок 1-го класса,
а также бистальных 2-го класса при
выполнении требований 8.3.6, 9.2.1 и 9.2.8 не превышает предельных значений
балок 1-го класса,
а также бистальных 2-го класса при
выполнении требований 8.3.6, 9.2.1 и 9.2.8 не превышает предельных значений ![]() , определяемых по формулам:
, определяемых по формулам:
для неокаймленного свеса двутаврового сечения
для поясного листа коробчатого сечения
![]() (83)
(83)
Здесь σс - напряжение в сжатом поясе, определяемое по формулам:
для однородного сечения
σс = M/(Wxncγc)
или σc = Mx/(Wxncγc) + My/(Wynγc);
для бистального сечения
![]()
или ![]() ,
,
где α' - значения α из таблицы 17 при τ = 0; если σc > σyf, то следует принимать σc = σyf.
9.5.15 Устойчивость сжатых поясов
считают обеспеченной, если условная гибкость свеса сжатого пояса или поясного
листа балок 2-го и 3-го классов из
однородной стали при выполнении требований 8.3.6, 9.2.3 и 9.5.8 не превышает предельных значений ![]() , определяемых при 2,2 ≤
, определяемых при 2,2 ≤ ![]() ≤ 5,5 по формулам:
≤ 5,5 по формулам:
для неокаймленного свеса двутаврового сечения
для поясного листа коробчатого сечения
![]() = 0,675
+ 0,15
= 0,675
+ 0,15![]() . (85)
. (85)
9.5.16 В случае окаймления свеса ребром (рисунок 5), имеющим размер aef ≥ 0,3bef и толщину ![]() , значения
, значения ![]() , определяемые по формулам (82) и (84), допускается увеличивать в 1,5 раза.
, определяемые по формулам (82) и (84), допускается увеличивать в 1,5 раза.
9.6 РАСЧЕТ ОПОРНЫХ ПЛИТ
9.6.1 Площадь стальной опорной плиты должна удовлетворять требованиям расчета на прочность фундамента.
Передача расчетного усилия на опорную плиту может осуществляться через фрезерованный торец опирающейся конструкции или через сварные швы.
9.6.2 Толщину опорной плиты определяют расчетом на изгиб пластинки по формуле
![]() (86)
(86)
где Mmax - наибольший из изгибающих моментов M, действующих на разных участках опорной плиты и определяемых по формулам:
для консольного участка плиты
M = 0,5qc2; (87)
для участка плиты, опертого на три, четыре или две взаимно перпендикулярные стороны
M = αqb2, (88)
здесь c - вылет консольного участка плиты;
α - коэффициент, зависящий от условий опирания и отношения размеров сторон участка плиты;
q - реактивный отпор фундамента под рассматриваемым участком плиты на единицу площади плиты, принимаемый равномерным и равным среднему значению;
b - размер пластинки.
При определении изгибающего момента M для рассматриваемого участка плиты допускается учитывать разгружающее влияние смежных консольных участков вдоль длинных сторон по формуле
M = q(αb2 - 0,5c2). (89)
10 РАСЧЕТ ЭЛЕМЕНТОВ СТАЛЬНЫХ КОНСТРУКЦИЙ ПРИ ДЕЙСТВИИ ПРОДОЛЬНОЙ СИЛЫ С ИЗГИБОМ
10.1 РАСЧЕТ НА ПРОЧНОСТЬ ЭЛЕМЕНТОВ СПЛОШНОГО СЕЧЕНИЯ
10.1.1 Расчет на прочность внецентренно сжатых (сжато-изгибаемых) и внецентренно растянутых (растянуто-изгибаемых) элементов из стали с нормативным сопротивлением Ryn ≤ 440 Н/мм2, не подвергающихся непосредственному воздействию динамических нагрузок, при напряжениях τ < 0,5Rs и σ = N/An > 0,1Ry выполняют по формуле
где N, Mx и My - абсолютные значения соответственно продольной силы и изгибающих моментов при наиболее неблагоприятном их сочетании;
n, cx, cy - коэффициенты, принимаемые согласно таблице К.1 приложения К.
Если σ = N/An ≤ 0,1Ry, формулу (90) применяют при выполнении требований 9.5.8 и 9.5.14.
Расчет на прочность элементов в случаях, не предусмотренных расчетом по формуле (90), выполняют по формуле
(N/An ± Mxy/Ixn ± Myx/Iyn)/(Ryγc) ≤ 1, (91)
где x, y - расстояния от главных осей до рассматриваемой точки сечения.
10.1.2 Расчет на прочность внецентренно сжатых элементов по формуле (90) выполнять не требуется при значении приведенного относительного эксцентриситета mef ≤ 20 (10.2.2), отсутствии ослабления сечения и одинаковых значениях изгибающих моментов, принимаемых в расчетах на прочность и устойчивость.
10.1.3 Внецентренно сжатые элементы из стали с нормативным сопротивлением Ryn > 440 Н/мм2, имеющие несимметричные сечения относительно оси, перпендикулярной плоскости изгиба (например, сечения типа 10, 11 по таблице Ж.2 приложения Ж), проверяют на прочность растянутого волокна в плоскости действия момента по формуле
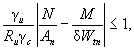 (92)
(92)
где Wtn - момент сопротивления сечения, вычисленный для растянутого волокна;
δ - коэффициент, определяемый по формуле
δ = 1 - 0,1N![]() /(ARy). (93)
/(ARy). (93)
10.2 РАСЧЕТ НА УСТОЙЧИВОСТЬ ЭЛЕМЕНТОВ СПЛОШНОГО СЕЧЕНИЯ
10.2.1 Расчет на устойчивость внецентренно сжатых элементов при действии момента в одной из главных плоскостей выполняют как в этой плоскости (плоская форма потери устойчивости), так и из этой плоскости (изгибно-крутильная форма потери устойчивости).
10.2.2 Расчет на устойчивость внецентренно сжатых элементов постоянного сечения в плоскости действия момента, совпадающей с плоскостью симметрии, следует выполнять по формуле
N/(φeARyγc) ≤ 1. (94)
В формуле (94)
коэффициент устойчивости при сжатии с изгибом φe определяют по таблице Ж.3
приложения Ж в зависимости от
условной гибкости ![]() и приведенного
относительного эксцентриситета mef, определяемого по
формуле
и приведенного
относительного эксцентриситета mef, определяемого по
формуле
mef = ηm, (95)
где η - коэффициент влияния формы сечения, определяемый по таблице Ж.2 приложения Ж;
m = eA/Wc - относительный эксцентриситет (здесь e = M/N - эксцентриситет, при вычислении которого значения M и N принимают согласно требованиям 10.2.3; Wc - момент сопротивления сечения, вычисленный для наиболее сжатого волокна).
При значениях mef > 20 расчет выполняют как для изгибаемых элементов (раздел 9).
10.2.3 Расчетные значения продольной силы N и изгибающего момента M в элементе принимают для одного и того же сочетания нагрузок из расчета системы по недеформированной схеме в предположении упругих деформаций стали.
При этом значения M принимают равными:
для колонны постоянного сечения рамной системы - наибольшему моменту в пределах длины колонны;
для ступенчатой колонны - наибольшему моменту на длине участка постоянного сечения;
для колонны с одним защемленным, а другим свободным концом - моменту в заделке, но не менее момента в сечении, отстоящем на треть длины колонны от заделки;
для сжатых поясов ферм и структурных плит, воспринимающих внеузловую поперечную нагрузку, - наибольшему моменту в пределах средней трети длины панели пояса, определяемому из расчета пояса как упругой неразрезной балки;
для сжатого стержня с шарнирно-опертыми концами и сечением, имеющим ось симметрии, совпадающую с плоскостью изгиба, - моменту, определяемому по формулам таблицы 18 в зависимости от относительного эксцентриситета mmax = MmaxA/(NWc) и принимаемому равным не менее 0,5Mmax.
Для сжатых стержней двоякосимметричного сплошного сечения с шарнирно-опертыми концами, на которых действуют изгибающие моменты, значение mef, необходимое для определения φe, принимают согласно таблице Ж.5 приложения Ж.
10.2.4 Расчет на устойчивость внецентренно сжатых сплошностенчатых стержней постоянного сечения (кроме коробчатого - 10.2.10) из плоскости действия момента при изгибе их в плоскости наибольшей жесткости (Ix > Iy), совпадающей с плоскостью симметрии, а также швеллеров выполняют по формуле
N/(cφyARyγc) ≤ 1, (96)
где c - коэффициент, определяемый согласно требованиям 10.2.5;
φy - коэффициент устойчивости при центральном сжатии, определяемый согласно требованиям 8.1.3.
10.2.5 Коэффициент c в формуле (96) определяют:
при значениях mx ≤ 5 по формуле
c = β/(1 + αvmx) ≤ 1, (97)
где α, β и v - коэффициенты, определяемые по таблице 19;
при значениях mx ≥ 10 по формуле
c = 1/(1 + mxφy/φb), (98)
где φb - коэффициент устойчивости при изгибе, определяемый согласно требованиям 9.4.1 и приложению М как для балки с двумя и более закреплениями сжатого пояса;
при значениях 5 < mx < 10 по формуле
c = c5(2 - 0,2mx) + c10(0,2mx - 1), (99)
где определяют: c5 - по формуле (97) при mx = 5;
c10 - по формуле (98) при mx = 10.
Здесь mx = (Mx/N)(A/Wc) - относительный эксцентриситет, при вычислении которого Mx принимают согласно требованиям 10.2.6.
При гибкости ![]() > 3,14 коэффициент c не должен превышать значений cmax, определяемых согласно
приложению И; в случае если c > cmax, в формулах (96) и (101) вместо c принимают cmax.
> 3,14 коэффициент c не должен превышать значений cmax, определяемых согласно
приложению И; в случае если c > cmax, в формулах (96) и (101) вместо c принимают cmax.
10.2.6 При определении относительного эксцентриситета mx в формулах (97) - (99) за расчетный момент Mx принимают:
для стержней с концами, закрепленными от смещения перпендикулярно плоскости действия момента, - максимальный момент в пределах средней трети длины (но не менее половины наибольшего по длине стержня момента);
для стержней с одним защемленным, а другим свободным концом - момент в заделке (но не менее момента в сечении, отстоящем на треть длины стержня от заделки).
10.2.7 Расчет на устойчивость внецентренно сжатых элементов двутаврового сечения, непрерывно подкрепленных вдоль одной из полок, выполняют согласно приложению М.
Таблица 18
|
mmax |
Момент M при условной гибкости стержня |
|
|
|
|
|
|
mmax ≤ 3 |
M = Mmax - 0,25 |
M = M1 |
|
3 < mmax ≤ 20 |
M = M2 + (mmax - 3)(Mmax - M2)/17 |
M = M1 + (mmax - 3)(Mmax - M1)/17 |
|
Обозначения, принятые в таблице 18: Mmax - наибольший изгибающий момент в пределах длины стержня; M1 - наибольший изгибающий момент в пределах средней трети длины стержня, принимаемый равным не менее 0,5Mmax; M2 - изгибающий
момент, принимаемый равным M при mmax ≤ 3 и |
||
Таблица 19
|
Тип сечения |
Схема сечения и эксцентриситет |
Значения коэффициентов |
||||
|
α при |
β при |
v |
||||
|
m ≤ 1 |
1 < m ≤ 5 |
|
|
|||
|
1 |
|
0,7 |
0,65 + 0,05mx |
1 |
|
1 -
( |
|
2 |
|
1 |
||||
|
3 |
|
1,25 - 0,12 |
||||
|
4 |
|
1 - 0,3I2/I1 |
1 - (0,35 - 0,05mx)I2/I1 |
1 |
1 - (1 -
β = 1 при I2/I1 < 0,5 |
1 |
|
Обозначения, принятые в таблице 19: I1 и I2 - моменты инерции соответственно большей и меньшей полок относительно оси симметрии сечения y-y; φc - значение φy при Примечание - При значениях b/h < 0,3 принимают b/h = 0,3. |
||||||
10.2.8 Внецентренно сжатые элементы постоянного сечения, изгибаемые в плоскости наименьшей жесткости (Iy < Ix и ey ≠ 0), рассчитывают по формуле (94), а при гибкости λх > λу также проверяют расчетом на устойчивость из плоскости действия момента как центрально-сжатые элементы по формуле
N/(φxARyγc) ≤ 1, (100)
где φx - коэффициент устойчивости при центральном сжатии, определяемый согласно требованиям 8.1.3.
При λx ≤ λy проверки устойчивости из плоскости действия момента не требуется.
10.2.9 Расчет на устойчивость сплошностенчатых стержней постоянного сечения (кроме коробчатого), подверженных сжатию и изгибу в двух главных плоскостях, при совпадении плоскости наибольшей жесткости (Ix > Iy) с плоскостью симметрии, а также при сечении типа 3 (таблица 19) выполняют по формуле
N/(φexyARyγc) ≤ 1, (101)
где φexy = cφeyψ.
Здесь определяют: c - согласно требованиям 10.2.5;
φey - согласно требованиям 10.2.2
с заменой в формулах m и ![]() соответственно на my и
соответственно на my и ![]() ;
;
ψ - по формулам:
для сечений типов 1 и 3 (таблица 19) при mx ≤ 5 и my ≤ 5
ψ = 1 + 0,65(1 - 0,02![]() )
)![]() mxmy; (102)
mxmy; (102)
для сечений типов 1 и 3 при mx > 5 и my > 5, а также для сечений типов 2 и 4 (таблица 19)
![]() (103)
(103)
При вычислении значения mef,y = ηmy для стержней двутаврового сечения с неодинаковыми полками коэффициент η определяют как для сечения типа 8 по таблице Ж.2 приложения Ж.
Если mef,y < mx, то кроме расчета по формуле (101) выполняют расчет по формулам (94) и (96), принимая ey = 0.
Если λx > λy, то кроме расчета по формуле (101) выполняют расчет по формуле (94), принимая ey = 0.
Значения относительных эксцентриситетов вычисляют по формулам:
mx = exA/Wcx и my = eyA/Wcy, (104)
где Wcx и Wcy - моменты сопротивления сечений для наиболее сжатого волокна относительно осей соответственно x-x и y-y.
Если плоскость наибольшей жесткости сечения стержня (Ix > Iy) не совпадает с плоскостью симметрии, то расчетное значение mx увеличивают на 25 % (кроме сечения типа 3 по таблице 19).
10.2.10 Расчет на устойчивость сплошностенчатых стержней постоянного коробчатого сечения при сжатии с изгибом в одной или в двух главных плоскостях выполняют по формулам:
N/(φeyARyγc) + Mx/(cxδxWx,minRyγc) ≤ 1; (105)
N/(φexARyγc) + My/(cyδyWy,minRyγc) ≤ 1, (106)
где φex, φey - коэффициенты устойчивости при сжатии с изгибом, определяемые по таблице Ж.3 приложения Ж;
cx, cy - коэффициенты, принимаемые по таблице К.1 приложения К;
δx, δy - коэффициенты, определяемые по формулам:
δx = 1 - 0,1N![]() /(ARy)
и δy = 1 - 0,1N
/(ARy)
и δy = 1 - 0,1N![]() /(ARy) (107)
/(ARy) (107)
и принимаемые
равными 1,0
соответственно при ![]() ≤ 1 и
≤ 1 и ![]() ≤ 1.
≤ 1.
При одноосном изгибе в плоскости наибольшей жесткости (Ix > Iy; My = 0) вместо φey принимают φy.
10.3 РАСЧЕТ НА УСТОЙЧИВОСТЬ ЭЛЕМЕНТОВ СКВОЗНОГО СЕЧЕНИЯ
10.3.1 Расчет на устойчивость внецентренно сжатых стержней сквозного сечения с соединительными планками или решетками выполняют как расчет стержня в целом, так и отдельных ветвей.
10.3.2 При расчете стержня в целом относительно свободной оси по формуле
(94), когда планки и решетки расположены в плоскостях, параллельных
плоскости действия момента, коэффициент φe определяют по таблице Ж.4 приложения Ж в зависимости от условной приведенной
гибкости ![]() (λef по таблице 7) и относительного эксцентриситета m,
определяемого по
формуле
(λef по таблице 7) и относительного эксцентриситета m,
определяемого по
формуле
m = eAa/I, (108)
где e = M/N - эксцентриситет, при вычислении которого значения M и N принимают согласно требованиям 10.2.3;
a - расстояние от главной оси сечения, перпендикулярной плоскости действия момента, до оси наиболее сжатой ветви, но не менее расстояния до оси стенки ветви;
I - момент инерции сечения сквозного стержня относительно свободной оси.
При значениях m > 20 расчет выполняют как для изгибаемых элементов.
10.3.3 При расчете отдельных ветвей сквозных стержней с решетками по формуле (7) продольную силу в каждой ветви определяют с учетом дополнительного усилия Nad от момента M, которое определяют по формулам:
Nad = My/b - при изгибе стержня в плоскости, перпендикулярной оси y-y, для сечений типов 1 и 3 (таблица 7);
Nad = 0,5My/b1 - то же, для сечений типа 2 (таблица 7);
Nad = 1,16Mx/b - при изгибе стержня в плоскости, перпендикулярной оси x-x, для типов 1 и 3 (таблица 7);
Nad = 0,5My/b1 - то же, для сечений типа 2 (таблица 7);
Nad = 1,16Mx/b - при изгибе стержня в плоскости, перпендикулярной оси x-x, для сечений типа 3 (таблица 7);
Nad = 0,5Mx/b2 - то же, для сечений типа 2 (таблица 7).
Здесь b, b1, b2 - расстояния между осями ветвей (таблица 7).
При изгибе стержня сквозного сечения типа 2 (таблица 7) в двух плоскостях усилие Nad определяют по формуле
Nad = 0,5(My/b1 + Mx/b2). (109)
10.3.4 При расчете отдельных ветвей сквозных стержней с планками в формуле (94) учитывают дополнительное усилие Nad от момента M и местный изгиб ветвей от фактической или условной поперечной силы (как в поясах безраскосной фермы).
10.3.5 Расчет на устойчивость внецентренно сжатых трехгранных сквозных стержней с решетками и постоянным по длине равносторонним сечением выполняют согласно требованиям раздела 17.
10.3.6 Расчет на устойчивость сквозных стержней из двух сплошностенчатых ветвей, симметричных относительно оси x-x (рисунок 10), с решетками в двух параллельных плоскостях, подверженных сжатию и изгибу в обеих главных плоскостях, выполняют:
для стержня в целом - в плоскости, параллельной плоскостям решеток, согласно требованиям 10.3.2, принимая ex = 0;
для отдельных ветвей - как внецентренно сжатых элементов по формулам (94) и (96); при этом продольную силу в каждой ветви определяют с учетом дополнительного усилия от момента My (10.3.3), а момент Mx распределяют между ветвями пропорционально их жесткостям Ixв (рисунок 10); если момент Mx действует в плоскости одной из ветвей, то считают его полностью передающимся на эту ветвь. При расчете по формуле (94) гибкость отдельной ветви определяют с учетом требований 11.2.14, а при расчете по формуле (96) - по максимальному расстоянию между узлами решетки.
Рисунок 10 - Схема сквозного сечения стержня из двух сплошностенчатых ветвей
10.3.7 Расчет соединительных планок или решеток сквозных внецентренно сжатых стержней выполняют согласно требованиям 8.2.8 и 8.2.9 на поперечную силу, равную большему из двух значений: фактической поперечной силе Q или условной поперечной силе Qfic, вычисляемой согласно требованиям 8.2.7.
В случае, когда фактическая поперечная сила больше условной, соединяют ветви сквозных внецентренно сжатых элементов, как правило, решетками.
10.4 ПРОВЕРКА УСТОЙЧИВОСТИ СТЕНОК И ПОЯСОВ
10.4.1 Расчетные размеры проверяемых на устойчивость стенок и поясных листов (полок) принимают согласно требованиям 8.3.1 и 8.3.6.
10.4.2 Устойчивость стенок внецентренно сжатых элементов считают
обеспеченной, если условная гибкость стенки ![]() не превышает значений предельной условной гибкости
не превышает значений предельной условной гибкости ![]() , определяемых по формулам таблицы 20.
, определяемых по формулам таблицы 20.
Таблица 20
|
Схема сечения и эксцентриситет |
Условия применения формул |
Предельная
условная гибкость стенки |
||
|
1 |
|
1 ≤ mx ≤ 10; для двутавра cφy > φe |
|
|
|
|
||||
|
2 |
|
cφy ≤ φe; 1≤ α ≤2 |
|
|
|
3 |
|
1 ≤ α ≤ 2 |
|
|
|
4 |
|
1 ≤ bf/hef ≤ 2; 0,8 ≤ |
|
|
|
5 |
|
my ≥ 1 |
|
|
|
Обозначения, принятые в таблице 20:
ccr - коэффициент, определяемый по таблице 16 в зависимости от α; α = (σ1 - σ2)/σ1 (здесь σ1 - наибольшее сжимающее напряжение у расчетной границы стенки, принимаемое со знаком «плюс» и вычисленное без учета коэффициентов φe, cφy и φexy; σ2 - соответствующее напряжение у противоположной расчетной границы стенки); β = 0,15ccrτ/σ1 (здесь τ = Q/(twhw) - среднее касательное напряжение в рассматриваемом сечении; для коробчатого сечения τ = Q/(2twhw); bf - ширина полки тавра. Примечания 1 Для
сечений типа 1 при значениях 0 < mx < 1 или
10 < mx < 20 значения 2 При
α ≤ 0,5 значение При 0,5 < α < 1
значения 3 Для
сечений типа 4 при 4 Для
сечений типа 5 при значениях 0 < my < 1
значения |
||||
10.4.3 При выполнении условия 0,8 ≤ N/(φeARyγc) ≤ 1 предельную
условную гибкость ![]() , вычисленную по формулам (110) и (111) таблицы 20, допускается увеличивать путем определения ее по формуле
, вычисленную по формулам (110) и (111) таблицы 20, допускается увеличивать путем определения ее по формуле
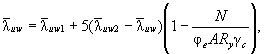 (116)
(116)
где ![]() и
и ![]() - значения
- значения ![]() , вычисленные по формулам (110), (111) и (112)
таблицы 20.
, вычисленные по формулам (110), (111) и (112)
таблицы 20.
При выполнении условия N/(φeARyγc) < 0,8 значение ![]() принимают равным
принимают равным ![]() .
.
10.4.4 Стенки внецентренно сжатых
элементов сплошного сечения (колонн, стоек, опор и т.п.) при ![]() , как правило, укрепляют поперечными ребрами жесткости в
соответствии с требованиями 8.3.3.
, как правило, укрепляют поперечными ребрами жесткости в
соответствии с требованиями 8.3.3.
10.4.5 При укреплении стенки внецентренно сжатого элемента продольным ребром жесткости (с моментом инерции Irl ≥ 6heftw3), расположенным посередине стенки, наиболее нагруженную часть стенки между поясом и осью ребра рассматривают как самостоятельную пластинку и проверяют по формулам таблицы 20. При этом расчет и проектирование ребра и элемента в целом выполняют с учетом требований 8.3.4.
10.4.6 В случаях, когда фактическое значение условной гибкости стенки ![]() превышает предельное
значение
превышает предельное
значение ![]() , вычисленное для сечений типа 1 по формулам таблицы 20,
а для сечений типов 2 и 3 с учетом примечания 2
таблицы 20 (при α ≤
0,5),
допускается проверку устойчивости стержня по формулам (94), (100)
и (101), а также по формуле (96) (при α ≤ 0,5) выполнять с учетом
расчетной уменьшенной площади Ad.
, вычисленное для сечений типа 1 по формулам таблицы 20,
а для сечений типов 2 и 3 с учетом примечания 2
таблицы 20 (при α ≤
0,5),
допускается проверку устойчивости стержня по формулам (94), (100)
и (101), а также по формуле (96) (при α ≤ 0,5) выполнять с учетом
расчетной уменьшенной площади Ad.
10.4.7 Устойчивость поясов (полок) внецентренно
сжатых стержней с гибкостью 0,8 ≤ ![]() (
(![]() ) ≤ 4 считают обеспеченной,
если условная гибкость свеса пояса (полки)
) ≤ 4 считают обеспеченной,
если условная гибкость свеса пояса (полки) ![]() или поясного листа
или поясного листа ![]() не превышает значений предельной условной гибкости
не превышает значений предельной условной гибкости ![]() , определяемых по формулам таблицы
21.
, определяемых по формулам таблицы
21.
Таблица 21
|
Схема сечения и эксцентриситет |
Условия применения формул |
Предельная условная гибкость свеса пояса |
|
|
1 |
|
0 ≤ mx ≤ 5 |
|
|
2 |
|
|
|
|
3 |
|
- |
|
|
4 |
|
|
|
|
Обозначение, принятое в таблице 21:
Примечание - При значениях 5 < mx
≤ 20 значения |
|||
10.4.8 Для свесов поясов (полок), окаймленных ребрами (рисунок
5), значения предельной условной гибкости ![]() , определяемые по формулам таблицы 21, умножают на коэффициент 1,5.
, определяемые по формулам таблицы 21, умножают на коэффициент 1,5.
Размеры окаймляющего ребра определяют согласно требованиям 8.3.9.
10.4.9 При назначении сечений внецентренно сжатых элементов по
предельной гибкости значения предельных условных гибкостей стенки ![]() , определяемых
по формулам таблицы 20, а также
поясов
, определяемых
по формулам таблицы 20, а также
поясов ![]() , определяемых по формулам таблицы
21 и согласно требованиям 10.4.8, допускается увеличивать
умножением на коэффициент
, определяемых по формулам таблицы
21 и согласно требованиям 10.4.8, допускается увеличивать
умножением на коэффициент ![]() , но не более чем в 1,25 раза (здесь φm - меньшее из значений φe, cφy, φexy, использованное при проверке устойчивости элемента).
, но не более чем в 1,25 раза (здесь φm - меньшее из значений φe, cφy, φexy, использованное при проверке устойчивости элемента).
11 РАСЧЕТНЫЕ ДЛИНЫ И ПРЕДЕЛЬНЫЕ ГИБКОСТИ ЭЛЕМЕНТОВ СТАЛЬНЫХ КОНСТРУКЦИЙ
11.1 РАСЧЕТНЫЕ ДЛИНЫ ЭЛЕМЕНТОВ ПЛОСКИХ ФЕРМ, СВЯЗЕЙ И СТРУКТУРНЫХ КОНСТРУКЦИЙ
11.1.1 Расчетные длины сжатых элементов плоских ферм и связей в их плоскости lef и из плоскости lef,1 (рисунок 11, а, б, в, г), за исключением элементов, указанных в 11.1.2 и 11.1.3, принимают по таблице 22.
а - треугольная со стойками; б - раскосная; в - треугольная со шпренгелями; г - полураскосная треугольная; д - перекрестная
Рисунок 11 - Схемы решеток ферм для определения расчетных длин сжатых элементов (обозначения - см. таблицу 22)
Таблица 22
|
Направление продольного изгиба элемента фермы |
Расчетные длины lef и lef,1 |
|||
|
поясов |
опорных раскосов и опорных стоек |
прочих элементов решетки |
||
|
1 |
В плоскости фермы lef: |
|
|
|
|
а) для ферм, кроме указанных в позиции 1,б |
l |
l |
0,8l |
|
|
б) для ферм из одиночных уголков и ферм с прикреплением элементов решетки к поясам впритык |
l |
l |
0,9l |
|
|
2 |
В направлении, перпендикулярном плоскости фермы (из плоскости фермы) lef,1: |
|
|
|
|
а) для ферм, кроме указанных в позиции 2,б |
l1 |
l1 |
l1 |
|
|
б) для ферм с прикреплением элементов решетки к поясам впритык |
l1 |
l1 |
0,9l1 |
|
|
3 |
В любом направлении lef = lef,1 для ферм из одиночных уголков при одинаковых расстояниях между точками закрепления элементов в плоскости и из плоскости фермы |
0,85l |
l |
0,85l |
|
Обозначения, принятые в таблице 22 (рисунок 11): l - геометрическая длина элемента (расстояние между центрами ближайших узлов) в плоскости фермы; l1 - расстояние между узлами, закрепленными от смещения из плоскости фермы (поясами ферм, специальными связями, жесткими плитами покрытий, прикрепленными к поясу сварными швами или болтами, и т.п.). |
||||
11.1.2 Расчетную длину lef,1 элемента, по длине которого действуют сжимающие силы N1 и N2 (N1 > N2), из плоскости фермы (рисунок 12) определяют по формуле
lef,1 = (0,75 + 0,25N2/N1)l1. (120)
При этом расчет на устойчивость выполняют на усилие N1.
Расчетные длины lef и lef,1 элементов постоянного сечения, раскрепленных связями на участках равной длины и нагруженных различными усилиями на этих участках, допускается определять согласно таблице О.1 приложения О.
а - схема фермы; б - схема связей между фермами (вид фермы)
Рисунок 12 - Схемы для определения расчетной длины пояса из плоскости фермы (обозначения - см. таблицу 23)
Таблица 23
|
Расчетная длина lef,1 из плоскости фермы при поддерживающем элементе |
|||
|
растянутом |
неработающем |
сжатом |
|
|
Оба элемента не прерываются |
l |
0,7l1 |
l1 |
|
Поддерживающий элемент прерывается и перекрывается фасонкой: |
|
|
|
|
рассматриваемый элемент не прерывается |
0,7l1 |
l1 |
1,4l1 |
|
рассматриваемый элемент прерывается и перекрывается фасонкой |
0,7l1 |
- |
- |
|
Обозначения, принятые в таблице 23 (рисунок 12): l - расстояние между центрами узлов фермы и пересечения элементов; l1 - полная геометрическая длина элемента. |
|||
11.1.3 Расчетные длины lef и lef,1 элементов перекрестной решетки, скрепленных между собой (рисунок 11, д), принимают:
в плоскости фермы - равными расстоянию между центрами узлов фермы и пересечения элементов (lef = l);
из плоскости фермы: для сжатых элементов - по таблице 23; для растянутых элементов - равными полной геометрической длине элемента (lef,1 = l).
11.1.4 Радиусы инерции i сечений элементов из одиночных уголков при определении гибкости принимают:
при расчетной длине элемента не менее 0,85l (где l - расстояние между центрами ближайших узлов) - минимальными (i = imin);
в остальных случаях - относительно оси уголка, перпендикулярной или параллельной плоскости фермы (i = ix или i = iy в зависимости от направления продольного изгиба).
11.1.5 Расчетные длины lef элементов структурных конструкций принимают по таблице 24.
Таблица 24
|
№ п.п. |
Элементы структурных конструкций |
Расчетная длина lef |
|
1 |
Кроме указанных в позициях 2 и 3 |
l |
|
2 |
Неразрезные (не прерывающиеся в узлах) пояса, а также элементы поясов и решеток, прикрепляемых в узлах сваркой впритык к шаровым или цилиндрическим узловым элементам |
0,85l |
|
3 |
Из одиночных уголков, прикрепляемых в узлах одной полкой: |
|
|
сварными швами или болтами (не менее двух), расположенными вдоль элемента, при l/imin: |
|
|
|
до 90 |
l |
|
|
св. 90 до 120 |
0,90l |
|
|
» 120 » 150 (только для элементов решетки) |
0,75l |
|
|
» 150 » 200 (только для элементов решетки) |
0,70l |
|
|
одним болтом при l/imin: |
|
|
|
до 90 |
l |
|
|
св. 90 до 120 |
0,95l |
|
|
» 120 » 150 (только для элементов решетки) |
0,85l |
|
|
» 150 » 200 (только для элементов решетки) |
0,80l |
|
|
Обозначение, принятое в таблице 24: l - геометрическая длина элемента (расстояние между центрами узлов структурной конструкции). |
||
Радиусы инерции сечений i элементов структурных конструкций при определении гибкости принимают:
для сжато-изгибаемых элементов - относительно оси, перпендикулярной или параллельной плоскости изгиба (i = ix или i = iy);
в остальных случаях - минимальными (i = imin).
11.2 РАСЧЕТНЫЕ ДЛИНЫ ЭЛЕМЕНТОВ ПРОСТРАНСТВЕННЫХ РЕШЕТЧАТЫХ КОНСТРУКЦИЙ
11.2.1 Расчетные длины lef и радиусы инерции сечений i сжатых и ненагруженных элементов пространственных конструкций (рисунок 13) из одиночных уголков при определении гибкости принимают по таблице 25 с учетом таблиц 26 и 27.
а, б, в - с совмещенными в смежных гранях узлами; г, д - с не совмещенными в смежных гранях узлами; е - с частично совмещенными в смежных гранях узлами
Рисунок 13 - Схемы пространственных решетчатых конструкций (обозначения - см. таблицы 25, 26)
Расчетные длины lef и радиусы инерции i растянутых элементов из одиночных уголков при определении гибкости принимают:
для поясов - по таблице 25;
для перекрестных раскосов по рисунку 13, а, д - в плоскости грани - равными длине ld и радиусу инерции imin; из плоскости грани - равными полной длине раскоса ld1 и радиусу инерции ix относительно оси, параллельной плоскости грани;
для раскосов по рисунку 13, б, в, г, е - равными длине ld и радиусу инерции imin.
Таблица 25
|
lef |
i |
|
|
Пояса: |
|
|
|
по рисунку 13, а, б, в |
lm |
imin |
|
по рисунку 13, г, д |
0,73lm |
imin |
|
по рисунку 13, е |
0,64lm |
imin |
|
Раскосы: |
|
|
|
по рисунку 13, а, д |
μdldc |
imin |
|
по рисунку 13, б, в, г, е |
μdld |
imin |
|
Распорки: |
|
|
|
по рисунку 13, б, е |
0,80lc |
imin |
|
по рисунку 13, в |
0,73lc |
imin |
|
Обозначения, принятые в таблице 25 (рисунок 13): ldc - условная длина, принимаемая по таблице 26; μd - коэффициент расчетной длины раскоса, принимаемый по таблице 27. Примечания 1 Раскосы по рисунку 13, а, д в точках пересечения должны быть скреплены между собой. 2 Значение lef для распорок по рисунку 13, в дано для равнополочных уголков. |
||
Таблица 26
|
Конструкция узла пересечения элементов решетки |
Условная длина раскоса ldc при поддерживающем элементе |
||
|
растянутом |
неработающем |
сжатом |
|
|
Оба стержня не прерываются |
ld |
1,3ld |
0,8ld1 |
|
Поддерживающий элемент прерывается и перекрывается фасовкой, рассматриваемый элемент не прерывается: |
|
|
|
|
в конструкциях по рисунку 13, а |
1,3ld |
1,6ld |
ld1 |
|
то же, 13, д |
(1,75 - 0,15n)ld |
(1,9 - 0,1n)ld |
ld1 |
|
Узел пересечения элементов закреплен от смещения из плоскости грани (диафрагмой и т.п.) |
ld |
ld |
ld |
|
Обозначение, принятое в таблице 26 (рисунок 13): n = Im,minld/(Id,minlm), где Im,min и Id,min - наименьшие моменты инерции сечения соответственно пояса и раскоса. Примечание - При n < 1 и n > 3 в формулах таблицы 26 принимают соответственно n = 1 и n = 3. |
|||
Таблица 27
|
Значение n |
Значение μd при l/imin, равном |
|||
|
до 60 |
св. 60 до 160 |
св. 160 |
||
|
Сварными швами, болтами (не менее двух), расположенными вдоль раскоса |
До 2 |
1,14 |
0,54 + 36imin/l |
0,765 |
|
Св. 6 |
1,04 |
0,54 + 28,8imin/l |
0,740 |
|
|
Одним болтом |
При любых значениях |
1,12 |
0,64 + 28,8imin/l |
0,820 |
|
Обозначения, принятые в таблице 27: n - по таблице 26; l - длина, принимаемая равной: ld - для раскосов по рисунку 13, б, в, г, е; ldc по таблице 26 - для раскосов по рисунку 13, а, д. Примечания 1 Значение μd при 2 ≤ n ≤ 6 определяют линейной интерполяцией. 2 При прикреплении одного конца раскоса к поясу без фасонок сваркой или болтами, а второго конца - через фасонку коэффициент расчетной длины раскоса принимают равным 0,5(1 + μd); при прикреплении обоих концов раскосов через фасонки - μd = 1,0. 3 Концы раскосов по рисунку 13, в крепят, как правило, без фасонок. В этом случае при их прикреплении к распорке и поясу сварными швами или болтами (не менее двух), расположенными вдоль раскоса, значение коэффициента μd принимают при значении n «до 2». В случае прикрепления их концов одним болтом значение μd принимают по строке «одним болтом», а при вычислении значения lef согласно таблице 25 вместо μd принимают 0,5(1 + μd). |
||||
11.2.2 Расчетные длины lef и радиусы инерции i элементов из труб или парных уголков принимают согласно требованиям 11.1.1 - 11.1.3.
11.2.3 Расчетные длины сжатых элементов пространственных решетчатых конструкций допускается определять из расчета с использованием сертифицированных вычислительных комплексов (в предположении упругой работы стали и недеформированной схемы).
11.3 РАСЧЕТНЫЕ ДЛИНЫ КОЛОНН (СТОЕК)
11.3.1 Расчетные длины lef колонн (стоек) постоянного сечения или отдельных участков ступенчатых колонн определяют по формуле
lef = μl, (121)
где l - длина колонны, стального участка ее или высоты этажа;
μ - коэффициент расчетной длины.
11.3.2 При определении коэффициентов расчетной длины колонн (стоек) значения продольных сил в элементах системы принимают, как правило, для того сочетания нагрузок, для которого выполняется проверка устойчивости колонн (стоек) согласно требованиям разделов 8 и 10 настоящего Свода правил.
Допускается определять коэффициенты расчетной длины колонн постоянного сечения и отдельных участков ступенчатых колонн лишь для сочетания нагрузок, дающего наибольшие значения продольных сил в колоннах и на отдельных участках, и полученные значения коэффициента μ использовать для других сочетаний нагрузок.
При этом необходимо различать несвободные (раскрепленные) и свободные (нераскрепленные) рамы. В первом случае узлы крепления ригелей к колоннам не имеют свободы перемещения в плоскости рамы; во втором случае такие перемещения возможны.
11.3.3 Коэффициенты расчетной длины μ колонн (стоек) постоянного сечения определяют в зависимости от условий закрепления их концов и вида нагрузки. Для некоторых случаев закрепления концов и вида нагрузки значения μ приведены в таблице 28.
Коэффициенты расчетной длины колонн (стоек) постоянного сечения с упругим закреплением концов допускается определять по формулам, приведенным в таблице О.2 приложения О.
11.3.4 Коэффициенты расчетной длины μ колонн постоянного сечения в плоскости свободных и несвободных рам при жестком креплении ригелей к колоннам и при одинаковом нагружении узлов, расположенных в одном уровне, определяют по формулам таблицы 29.
11.3.5 Коэффициенты расчетной длины μ колонн (стоек) 1-го яруса однопролетных и многопролетных рам допускается определять согласно таблице О.4 приложения О.
11.3.6 При отношении H/B ³ 6 (где H - полная высота свободной многоэтажной рамы, B - ширина рамы) должна быть проверена общая устойчивость рамы в целом как составного стержня, защемленного в основании и свободного вверху.
Таблица 28
|
|
|
|
|
|
|
|
|
|
|
μ |
1,0 |
0,7 |
0,5 |
2,0 |
1,0 |
2,0 |
0,725 |
1,12 |
Таблица 29
|
Коэффициент μ |
|||
|
p |
n |
||
|
Свободные рамы |
|||
|
|
- |
|
|
|
|
- |
|
|
|
|
- |
|
|
|
|
- |
|
|
|
|
Верхний этаж |
При n ≤ 0,2 при n > 0,2
|
|
|
|
|
||
|
Средний этаж |
|||
|
|
|
||
|
Нижний этаж |
|||
|
|
|
||
|
|
Несвободные рамы |
|
|
|
Верхний этаж |
|||
|
0,5(p1 + р2) |
n1 + n2 |
||
|
Средний этаж |
|||
|
0,5(p1 + р2) |
0,5(n1 + n2) |
||
|
Нижний этаж |
|||
|
p1 + р2 |
0,5(n1 + n2) |
||
|
Обозначения, принятые в таблице 29: Is1, Is2 и Ii1, Ii2 - моменты инерции сечения ригелей, примыкающих соответственно к верхнему и нижнему концу проверяемой колонны; Ic, lc - соответственно момент инерции сечения и длина проверяемой колонны; l1, l2 - пролеты рамы; k - число пролетов;
Примечания 1 Для крайней колонны свободной многопролетной рамы коэффициент μ определяют при значениях p и n для колонн однопролетной рамы. 2 Для однопролетной многоэтажной рамы при вычислении p и n в формулах (124) - (126) принимают p2 = n2 = 0. |
|||
11.3.7 При неравномерном нагружении верхних узлов колонн в свободной одноэтажной раме и наличии жесткого диска покрытия или продольных связей по верху всех колонн коэффициент расчетной длины μef наиболее нагруженной колонны в плоскости рамы определяют по формуле
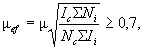 (127)
(127)
где μ - коэффициент расчетной длины проверяемой колонны, вычисленный по формулам (122) и (123) таблицы 29;
Ic, Nc - момент инерции сечения и усилие в наиболее нагруженной колонне рассматриваемой рамы соответственно;
ΣNi, ΣIi - сумма расчетных усилий и моментов инерции сечений всех колонн рассматриваемой рамы и четырех соседних рам (по две с каждой стороны) соответственно; все усилия находят при том же сочетании нагрузок, которое вызывает усилие Nc в проверяемой колонне.
11.3.8 Коэффициенты расчетной длины μ отдельных участков ступенчатых колонн в плоскости рамы определяют согласно приложению П.
При определении коэффициентов расчетной длины μ для ступенчатых колонн рам одноэтажных производственных зданий допускается:
не учитывать влияние степени загружения и жесткости соседних колонн;
для многопролетных рам (с числом пролетов два и более) при наличии жесткого диска покрытия или продольных связей, связывающих поверху все колонны и обеспечивающих пространственную работу сооружения, определять расчетные длины колонн как для стоек, неподвижно закрепленных на уровне ригелей.
11.3.9 При определении коэффициентов расчетных длин колонн рамных систем согласно 11.3.3 - 11.3.8 допускается учитывать влияние характера деформирования системы под нагрузкой в соответствии с приложением О.
11.3.10 Расчетные длины колонн в направлении вдоль здания (из плоскости рамы), как правило, принимают равными расстояниям между закрепленными от смещения из плоскости рамы точками (опорами колонн, подкрановых балок и подстропильных ферм, узлами крепления связей и ригелей и т.п.). Расчетные длины допускается определять на основе расчетной схемы, учитывающей фактические условия закрепления концов колонн.
11.3.11 Расчетную длину ветвей плоских опор транспортерных галерей принимают равной:
в продольном направлении галереи - высоте опоры (от низа базы до оси нижнего пояса фермы или балки), умноженной на коэффициент μ, определяемый как для стоек постоянного сечения в зависимости от условий закрепления их концов;
в поперечном направлении (в плоскости опоры) - расстоянию между центрами узлов; при этом должна быть проверена общая устойчивость опоры в целом как составного стержня, защемленного в основании и свободного вверху.
11.4 ПРЕДЕЛЬНЫЕ ГИБКОСТИ ЭЛЕМЕНТОВ
11.4.1 Гибкости элементов λ = lef/i, как правило, не должны превышать предельных значений λu, приведенных в таблице 30 для сжатых элементов и в таблице 31 - для растянутых.
Для элементов конструкций, которые согласно приложению В относятся к группе 4, в зданиях и сооружениях I и II уровней ответственности (согласно требованиям приложения 7* «Учет ответственности зданий и сооружений» к СНиП 2.01.07), а также для всех элементов конструкций в зданиях и сооружениях III уровня ответственности допускается повышать значение предельной гибкости на 10 %.
Таблица 30
|
Элементы конструкций |
Предельная гибкость сжатых элементов λu |
|
|
1 |
Пояса, опорные раскосы и стойки, передающие опорные реакции: |
|
|
плоских ферм, структурных конструкций и пространственных конструкций из труб или парных уголков высотой до 50 м |
180 - 60α |
|
|
пространственных конструкций из одиночных уголков, а также пространственных конструкций из труб и парных уголков высотой св. 50 м |
120 |
|
|
2 |
Элементы, кроме указанных в позициях 1 и 7: |
|
|
плоских ферм, сварных пространственных и структурных конструкций из одиночных уголков, пространственных и структурных конструкций из труб и парных уголков |
210 - 60α |
|
|
пространственных и структурных конструкций из одиночных уголков с болтовыми соединениями |
220 - 40α |
|
|
3 |
Верхние пояса ферм, не закрепленные в процессе монтажа (предельную гибкость после завершения монтажа следует принимать по позиции 1) |
220 |
|
4 |
Основные колонны |
180 - 60α |
|
5 |
Второстепенные колонны (стойки фахверка, фонарей и т.п.), элементы решетки колонн, элементы вертикальных связей между колоннами (ниже балок крановых путей) |
210 - 60α |
|
6 |
Элементы связей, кроме указанных в позиции 5, а также стержни, служащие для уменьшения расчетной длины сжатых стержней, и другие ненагруженные элементы, кроме указанных в позиции 7 |
200 |
|
7 |
Сжатые и ненагруженные элементы пространственных конструкций таврового и крестового сечений, подверженные воздействию ветровых нагрузок, при проверке гибкости в вертикальной плоскости |
150 |
|
Обозначение, принятое в таблице 30:
|
||
Таблица 31
|
№ п.п. |
Элементы конструкций |
Предельная гибкость растянутых элементов λu при воздействии на конструкцию нагрузок |
||
|
динамических, приложенных непосредственно к конструкции |
статических |
от кранов (см. примечание, позиция 5) и железнодорожных составов |
||
|
1 |
Пояса и опорные раскосы плоских ферм (включая тормозные фермы) и структурных конструкций |
250 |
400 |
250 |
|
2 |
Элементы ферм и структурных конструкций, кроме указанных в позиции 1 |
350 |
400 |
300 |
|
3 |
Нижние пояса балок и ферм крановых путей |
- |
- |
150 |
|
4 |
Элементы вертикальных связей между колоннами (ниже балок крановых путей) |
300 |
300 |
200 |
|
5 |
Прочие элементы связей |
400 |
400 |
300 |
|
6 |
Пояса и опорные раскосы стоек и траверс, тяги траверс опор линий электропередачи, открытых распределительных устройств и контактных сетей транспорта |
250 |
- |
- |
|
7 |
Элементы опор линий электропередачи, открытых распределительных устройств и контактных сетей транспорта, кроме указанных в позициях 6 и 8 |
350 |
- |
- |
|
8 |
Элементы пространственных конструкций таврового и крестового сечений (а в тягах траверс - опор линий электропередачи и из одиночных уголков), подверженных воздействию ветровых нагрузок, при проверке гибкости в вертикальной плоскости |
150 |
- |
- |
|
Примечания 1 В конструкциях, не подвергающихся динамическим воздействиям, гибкость растянутых элементов проверяют только в вертикальных плоскостях. 2 Для элементов связей, у которых прогиб под действием собственного веса не превышает l/150, при воздействии на конструкцию статических нагрузок допускается принимать λu = 500. 3 Гибкость растянутых элементов, подвергнутых предварительному напряжению, не ограничивается. 4 Значения предельных гибкостей принимают при кранах групп режимов работы 7К (в цехах металлургических производств) и 8К по ГОСТ 25546. 5 Для нижних поясов балок и ферм крановых путей при кранах групп режимов работы 1К - 6К допускается принимать λu = 200. 6 К динамическим нагрузкам, приложенным непосредственно к конструкции, относятся нагрузки, принимаемые в расчетах на усталость или с учетом коэффициентов динамичности. |
||||
12 РАСЧЕТ ЛИСТОВЫХ КОНСТРУКЦИЙ
12.1 РАСЧЕТ НА ПРОЧНОСТЬ
12.1.1 Расчет на прочность листовых конструкций (оболочек вращения), находящихся в безмоментном напряженном состоянии, выполняют по формуле
![]() (128)
(128)
где σx и σy - нормальные напряжения по двум взаимно перпендикулярным направлениям;
γc - коэффициент условий работы конструкций, назначаемый в соответствии с требованиями СНиП 2.09.03.
При этом абсолютные значения главных напряжений должны быть не более значений расчетных сопротивлений, умноженных на γc.
12.1.2 Напряжения в безмоментных тонкостенных оболочках вращения (рисунок 14), находящихся под давлением жидкости, газа или сыпучего материала, определяют по формулам:
![]() (129)
(129)
σ2 = (p/t - σ1/r1)r2, (130)
где σ1 и σ2 - меридиональное и кольцевое напряжения соответственно;
F - проекция на ось z-z оболочки полного расчетного давления, действующего на часть оболочки abc (рисунок 14);
r и β - радиус и угол, показанные на рисунке 14;
t - толщина оболочки;
p - расчетное давление на поверхность оболочки;
r1, r2 - радиусы кривизны в главных направлениях срединной поверхности оболочки.
Рисунок 14 - Схема оболочки вращения
12.1.3 Напряжения в замкнутых безмоментных тонкостенных оболочках вращения, находящихся под внутренним равномерным давлением, определяют по формулам:
для цилиндрических оболочек
σ1 = pr/(2t); σ2 = pr/t; (131)
для сферических оболочек
σ1 = σ2 = pr/(2t); (132)
для конических оболочек
![]()
![]() (133)
(133)
где p - расчетное внутреннее давление на поверхность оболочки;
r - радиус срединной поверхности оболочки (рисунок 15);
β - угол между образующей конуса и его осью z-z (рисунок 15).
Рисунок 15 - Схема конической оболочки вращения
12.1.4 При проверке прочности оболочек в местах изменения их формы или толщины, а также изменения нагрузки учитывают местные напряжения (краевой эффект).
12.2 РАСЧЕТ НА УСТОЙЧИВОСТЬ
12.2.1 Расчет на устойчивость замкнутых круговых цилиндрических оболочек вращения, равномерно сжатых параллельно образующим, выполняют по формуле
![]() (134)
(134)
где σ1 - расчетное напряжение в оболочке;
σcr,1 - критическое напряжение, равное меньшему из значений ψRy или cEt/r (здесь r - радиус срединной поверхности оболочки; t - толщина оболочки) при r/t ≤ 300; при r/t > 300 σcr,1 = cEt/r.
Значения коэффициента ψ при 0 < r/t ≤ 300 определяют по формуле
ψ = 0,97 - (0,00025 + 0,95Ry/E)r/t. (135)
Значения коэффициента c определяют по таблице 32.
Таблица 32
|
r/t |
100 |
200 |
300 |
400 |
600 |
800 |
1000 |
1500 |
2500 |
|
c |
0,22 |
0,18 |
0,16 |
0,14 |
0,11 |
0,09 |
0,08 |
0,07 |
0,06 |
В случае внецентренного сжатия параллельно образующим или чистого изгиба в диаметральной плоскости при касательных напряжениях в месте наибольшего момента, не превышающих значения 0,07E(t/r)3/2, напряжение σcr,1 увеличивают в (1,1 - 0,1σ'2/σ1) раза, где σ'2 - наименьшее напряжение (растягивающие напряжения считать отрицательными).
12.2.2 В трубах, рассчитываемых как сжатые или внецентренно сжатые
стержни при условной гибкости ![]() , должно быть выполнено условие
, должно быть выполнено условие
Такие трубы рассчитывают на устойчивость в соответствии с требованиями разделов 8 и 10 независимо от расчета на устойчивость стенок. Расчет на устойчивость стенок бесшовных или электросварных труб не требуется, если значения r/t не превышают половины значений, определяемых по формуле (136).
12.2.3 Цилиндрическая панель, опертая по двум образующим и двум дугам направляющей, равномерно сжатая вдоль образующих, при b2/(rt) ≤ 20 (где b - ширина панели, измеренная по дуге направляющей) должна быть рассчитана на устойчивость как пластинка по формулам:
при расчетном напряжении σ ≤ 0,8Ry
![]() (137)
(137)
при расчетном напряжении σ = Ry
![]() (138)
(138)
При 0,8Ry < σ < Ry наибольшее отношение b/t определяют линейной интерполяцией.
Если b2/(rt) > 20, то панель рассчитывают на устойчивость как оболочку согласно требованиям 12.2.1.
12.2.4 Расчет на устойчивость замкнутой круговой цилиндрической оболочки вращения при действии внешнего равномерного давления p на боковую поверхность выполняют по формуле
σ2/(σcr,2γc) ≤ 1, (139)
где σ2 = pr/t - расчетное кольцевое напряжение в оболочке;
σcr,2 - критическое напряжение, определяемое по формулам:
при 0,5 ≤ l/r ≤ 10
σcr,2 = 0,55E(r/l)(t/r)3/2; (140)
при l/r ≥ 20
σcr,2 = 0,17E(t/r)2; (141)
при 10 < l/r < 20 напряжение σcr,2 определяют линейной интерполяцией.
Здесь l - длина цилиндрической оболочки.
Та же оболочка, но укрепленная кольцевыми ребрами, расположенными с шагом s ≥ 0,5r между осями, должна быть рассчитана на устойчивость по формулам (139) - (141) с подстановкой в них значения s вместо l.
В этом случае должно быть удовлетворено условие устойчивости ребра
в своей плоскости как сжатого стержня согласно требованиям 8.1.3 при N = prs и расчетной длине стержня lef = 1,8r, при этом в сечение ребра включают участки оболочки шириной 0,65t![]() с каждой стороны от оси ребра, а условная гибкость стержня
с каждой стороны от оси ребра, а условная гибкость стержня ![]() не должна превышать 6,5.
не должна превышать 6,5.
При одностороннем ребре жесткости его момент инерции вычисляют относительно оси, совпадающей с ближайшей поверхностью оболочки.
12.2.5 Расчет на устойчивость замкнутой круговой цилиндрической оболочки вращения, подверженной одновременному действию нагрузок, указанных в 12.2.1 и 12.2.4, выполняют по формуле
(1/γc)(σ1/σcr,1 + σ2/σcr,2) ≤ 1, (142)
где σcr,1 вычисляют согласно требованиям 12.2.1 и σcr,2 - согласно требованиям 12.2.4.
12.2.6 Расчет на устойчивость конической оболочки вращения с углом конусности β ≤ 60°, сжатой силой N вдоль оси (рисунок 16), выполняют по формуле
N/(Ncrγc) ≤ 1, (143)
где Ncr - критическая сила, определяемая по формуле
Ncr = 6,28tσcr,1rmcos2β; (144)
здесь t - толщина оболочки;
σcr,1 - значение напряжения, вычисленное согласно требованиям 12.2.1 с заменой радиуса r радиусом rm, равным:
rm = (0,9r2 + 0,1r1)/cosβ. (145)
Рисунок 16 - Схема конической оболочки вращения под действием продольного усилия сжатия
12.2.7 Расчет на устойчивость конической оболочки вращения при действии внешнего равномерного давления р на боковую поверхность выполняют по формуле
σ1/(σcr,2γc) ≤ 1, (146)
здесь σ2 = prm/t - расчетное кольцевое напряжение в оболочке;
σcr,2 - критическое напряжение, определяемое по формуле
σcr,2 = 0,55E(rm/h)(t/rm)3/2, (147)
где rm - радиус, определяемый по формуле (145);
h - высота конической оболочки (между основаниями).
12.2.8 Расчет на устойчивость конической оболочки вращения, подверженной одновременному действию нагрузок, указанных в 12.2.6 и 12.2.7, выполняют по формуле
(1/γc)(N/Ncr + σ2/σcr,2) ≤ 1, (148)
где значения Ncr и σcr,2 вычисляют по формулам (144) и (147).
12.2.9 Расчет на устойчивость полной сферической оболочки (или ее сегмента) при r/t ≤ 750 и действии внешнего равномерного давления p, нормального к ее поверхности, выполняют по формуле
σ/(σcrγc) ≤ 1, (149)
где σ = pr/(2t) - расчетное напряжение;
σcr = 0,1Et/r - критическое напряжение, принимаемое равным не более Ry;
r - радиус срединной поверхности сферы.
13 РАСЧЕТ ЭЛЕМЕНТОВ СТАЛЬНЫХ КОНСТРУКЦИЙ НА УСТАЛОСТЬ
13.1 ОБЩИЕ ПОЛОЖЕНИЯ РАСЧЕТА
13.1.1 При проектировании стальных конструкций и их элементов (балки крановых путей, балки рабочих площадок, элементы конструкций бункерных и разгрузочных эстакад, конструкции под двигатели и др.), непосредственно воспринимающие многократно действующие подвижные, вибрационные или другого вида нагрузки с количеством циклов нагружений 105 и более, которые могут привести к явлению усталости, учитывают требования к материалу, технологии изготовления, применяя такие конструктивные решения, которые не вызывают значительной концентрации напряжений, и проверяют расчетом на усталость.
Количество циклов нагружений принимают по технологическим требованиям эксплуатации.
Расчет конструкций на усталость производят на действие нагрузок, устанавливаемых согласно требованиям СНиП 2.01.07.
Конструкции высоких сооружений (типа мачт, башен и т.п.), проверяемые на ветровой резонанс согласно требованиям СНиП 2.01.07, проверяют расчетом на усталость.
13.1.2 Расчет на усталость производят по формуле
где σmax - наибольшее по абсолютному значению напряжение в рассчитываемом элементе, вычисленное по сечению нетто без учета коэффициента динамичности и коэффициентов φ, φb, φe;
α - коэффициент, учитывающий количество циклов нагружений n, принимаемый при п ≥ 3,9 · 106 равным α = 0,77 и вычисляемый при n < 3,9 ´ 106 по формулам:
для групп элементов 1 и 2
α = 0,064(п/106)2 - 0,5(n/106) + 1,75; (151)
для групп элементов 3 - 8
α = 0,07(п/106)2 - 0,64(n/106) + 2,2; (152)
Rv - расчетное сопротивление усталости, принимаемое по таблице 33 в зависимости от временного сопротивления стали Run и групп элементов конструкций, приведенных в приложении Р;
γv - коэффициент, определяемый по таблице 34 в зависимости от напряженного состояния и коэффициента асимметрии напряжений ρ = σmin/σmax (здесь σmin - наименьшее по абсолютному значению напряжение в рассчитываемом элементе, вычисляемое так же, как σmax, и при том же загружении; при разнозначных напряжениях σmax и σmin значение ρ принимают со знаком «минус»).
При расчете по формуле (150) должно выполняться условие αRvγv ≤ Ru/γu.
Таблица 33
|
Значение Rv при нормативном значении временного сопротивления стали Run, Н/мм2 |
||||||
|
До 420 |
Св. 420 до 440 |
Св. 440 до 520 |
Св. 520 до 580 |
Св. 580 до 675 |
||
|
1 |
120 |
128 |
132 |
136 |
145 |
|
|
2 |
100 |
106 |
108 |
110 |
116 |
|
|
3 |
Для всех марок стали |
90 |
||||
|
4 |
То же |
75 |
||||
|
5 |
» |
60 |
||||
|
6 |
» |
45 |
||||
|
7 |
» |
36 |
||||
|
8 |
» |
27 |
||||
Таблица 34
|
Коэффициент асимметрии напряжений ρ |
Формулы для вычисления коэффициента γv |
|
|
Растяжение |
-1 ≤ ρ ≤ 0 |
2,5 1,5 - ρ |
|
0 < ρ ≤ 0,8 |
2,0 1,2 - ρ |
|
|
0,8 < ρ < 1 |
1,0 1 - ρ |
|
|
Сжатие |
-1 ≤ ρ < 1 |
2,0 1 - ρ |
13.1.3 Стальные конструкции и их элементы, непосредственно воспринимающие нагрузки с количеством циклов нагружений менее 105, проектируют с применением таких конструктивных решений, которые не вызывают значительной концентрации напряжений.
13.2 РАСЧЕТ БАЛОК КРАНОВЫХ ПУТЕЙ
13.2.1 Расчет на усталость балок крановых путей выполняют согласно требованиям 13.1.1 и 13.1.2 на действие крановых нагрузок, определяемых согласно СНиП 2.01.07. При этом принимают α = 0,77 при кранах групп режимов работы 7К (в цехах металлургических производств) и 8К по ГОСТ 25546 и α = 1,1 - в остальных случаях.
13.2.2 Расчет на усталость верхней зоны стенок составных балок крановых путей для кранов групп режимов работы 7К (в цехах металлургических производств) и 8К по ГОСТ 25546 выполняют по формуле
где Rv - расчетное сопротивление усталости, принимаемое для всех сталей равным соответственно для балок со сварными и фрикционными поясными соединениями Rv = 75 Н/мм2 и 96 Н/мм2 для сжатой верхней зоны стенки (сечения в пролете балки); Rv = 65 Н/мм2 и 89 Н/мм2 для растянутой верхней зоны стенки (опорные сечения неразрезных балок).
Значения напряжений в формуле (153) определяют по формулам 9.3.3 для крановых нагрузок, принимаемых в расчете на усталость.
14 ПРОЕКТИРОВАНИЕ СТАЛЬНЫХ КОНСТРУКЦИЙ С УЧЕТОМ ПРЕДОТВРАЩЕНИЯ ХРУПКОГО РАЗРУШЕНИЯ
14.1 При проектировании стальных конструкций исключают возможность хрупкого разрушения, возникающую вследствие неблагоприятного влияния сочетания следующих факторов:
пониженной температуры, при которой сталь в зависимости от ее химического состава, структуры и толщины проката переходит в хрупкое состояние;
действия подвижных, динамических и вибрационных нагрузок;
высоких местных напряжений, вызванных воздействием сосредоточенных нагрузок или деформаций деталей соединения, а также остаточных напряжений;
резких концентраторов напряжений, ориентированных поперек направления действия растягивающих напряжений.
14.2 Для предотвращения хрупкого разрушения конструкций:
выбирают сталь согласно требованиям 6.2;
по возможности избегают расположения сварных швов в зонах действия растягивающих напряжений, превышающих 0,4Ry;
принимают меры по снижению неблагоприятного влияния концентрации напряжений и наклепа, вызванных конструктивным решением или возникающих при различных технологических операциях (правка, гибка, гильотинная резка, продавливание отверстий и т.п.);
избегают пересечений сварных швов;
для сварных стыковых соединений применяют выводные планки и физические методы контроля качества швов;
учитывают, что конструкции со сплошной стенкой имеют меньше концентраторов напряжений, чем решетчатые;
в стыках элементов, перекрываемых накладками, фланговые швы не доводят до оси стыка не менее чем на 25 мм с каждой стороны;
применяют возможно меньшие толщины элементов сечения (особенно при гильотинной резке кромок и продавливании отверстий);
фасонки связей, вспомогательных и других второстепенных элементов крепят к растянутым элементам конструкций по возможности на болтах.
15 ПРОЕКТИРОВАНИЕ СОЕДИНЕНИЙ СТАЛЬНЫХ КОНСТРУКЦИЙ
15.1 СВАРНЫЕ СОЕДИНЕНИЯ
15.1.1 При проектировании стальных конструкций со сварными соединениями:
назначают минимальные размеры сварных швов с учетом требований 15.1.4 - 15.1.6, а также применяют минимально необходимое количество расчетных и конструктивных сварных швов;
обеспечивают свободный доступ к местам выполнения сварных соединений с учетом выбранного вида и технологии сварки.
15.1.2 Основные типы, конструктивные элементы и размеры сварных соединений принимают по ГОСТ 5264, ГОСТ 8713, ГОСТ 11533, ГОСТ 11534, ГОСТ 14771, ГОСТ 23518.
15.1.3 При выборе электродов, сварочной проволоки и флюсов учитывают группы конструкций и расчетные температуры, указанные в приложении Г.
15.1.4 При проектировании сварных соединений исключают возможность хрупкого разрушения конструкций с учетом требований раздела 14.
15.1.5 При проектировании тавровых и угловых сварных соединений элементов стальных конструкций с растягивающими напряжениями в направлении толщины проката с целью исключения возможности слоистого разрушения металла под сварным швом, как правило:
применяют стали для конструкций группы 1 согласно приложению В с пределом текучести до 375 Н/мм2, а также стали с гарантированными механическими свойствами в направлении толщины проката согласно требованиям ГОСТ 28870;
применяют сварочные материалы с пониженной прочностью и повышенной пластичностью; используют технологические приемы сварки, направленные на снижение остаточных сварочных напряжений; не применяют порошковую проволоку;
заменяют угловые соединения тавровыми, а в последних обеспечивают отношение ширины свеса к толщине элементов не менее 1; применяют разделки кромок, обеспечивающие снижение объема наплавленного металла.
15.1.6 Сварные стыковые соединения листовых деталей, как правило, проектируют прямыми с полным проваром и с применением выводных планок. В монтажных условиях допускается односторонняя сварка с подваркой корня и сварка на остающейся стальной подкладке.
15.1.7 Размеры сварных угловых швов и конструкция соединения должны удовлетворять следующим требованиям:
а) катет углового шва kf не должен превышать 1,2t, где t - наименьшая из толщин свариваемых элементов; катет шва, наложенного на закругленную кромку фасонного проката толщиной t, как правило, не должен превышать 0,9t;
б) катет углового шва kf должен удовлетворять требованиям расчета и быть, как правило, не меньше указанного в таблице 35; катет шва в тавровом двустороннем, а также в нахлесточном и угловом соединениях допускается принимать меньше указанного в таблице 35, но не менее 4 мм, при этом размеры шва должны обеспечивать несущую способность, определяемую расчетом, и дополнительным контролем должно быть установлено отсутствие дефектов, в том числе технологических трещин;
в) расчетная длина углового шва должна быть не менее 4kf и не менее 40 мм;
г) расчетная длина флангового шва должна быть не более 85βfkf, за исключением швов, в которых усилие действует на всем протяжении шва (здесь βf - коэффициент, принимаемый согласно таблице 36);
д) размер нахлестки должен быть не менее пяти толщин наиболее тонкого из свариваемых элементов;
е) соотношение размеров катетов угловых швов принимают, как правило, 1:1; при разных толщинах свариваемых элементов допускается принимать швы с неравными катетами; при этом катеты, примыкающие к более тонкому либо к более толстому элементу, должны удовлетворять требованиям соответственно 15.1.7, а либо 15.1.7, б;
ж) угловые швы выполняют с плавным переходом к основному металлу в конструкциях, возводимых в районах с расчетными температурами ниже минус 45 °С, а также в случаях, когда плавный переход обеспечивает повышение расчетного сопротивления усталости сварных соединений.
Таблица 35
|
Вид соединения |
Вид сварки |
Предел текучести стали, Н/мм2 |
Минимальный катет шва kf, мм, при толщине более толстого из свариваемых элементов t, мм |
||||||
|
4 - 5 |
6 - 10 |
11 - 16 |
17 - 22 |
23 - 32 |
33 - 40 |
41 - 80 |
|||
|
Тавровое: с двусторонними угловыми швами |
Ручная дуговая |
До 285 |
4 |
4 |
4 |
5 |
5 |
6 |
6 |
|
Св. 285 до 390 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
|
» 390 » 590 |
5 |
6 |
7 |
8 |
9 |
10 |
12 |
||
|
нахлесточное и угловое |
Механизированная |
До 285 |
3 |
4 |
4 |
5 |
5 |
6 |
6 |
|
Св. 285 до 390 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
||
|
» 390 » 590 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
|
Тавровое с односторонними угловыми швами |
Ручная дуговая |
До 375 |
5 |
6 |
7 |
8 |
9 |
10 |
12 |
|
Механизированная |
» 375 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
Примечания 1 В конструкциях из стали с пределом текучести свыше 590 Н/мм2, а также из всех сталей при толщине элементов более 80 мм минимальный катет швов принимают по специальным техническим условиям. 2 В конструкциях группы 4 минимальный катет односторонних угловых швов уменьшают на 1 мм при толщине свариваемых элементов до 40 мм и на 2 мм - при толщине элементов свыше 40 мм. |
|||||||||
Таблица 36
|
Положение шва |
Коэффициент |
Значения коэффициентов βf и βz при нормальных режимах сварки и катетах швов, мм |
||||
|
3 - 8 |
9 - 12 |
14 - 16 |
св. 16 |
|||
|
Автоматическая при d = 3 ÷ 5 |
В лодочку |
βf |
1,1 |
0,7 |
||
|
βz |
1,15 |
1,0 |
||||
|
Нижнее |
βf |
1,1 |
0,9 |
0,7 |
||
|
βz |
1,15 |
1,05 |
1,0 |
|||
|
Автоматическая и механизированная при d = 1,4 ÷ 2 |
В лодочку |
βf |
0,9 |
0,8 |
0,7 |
|
|
βz |
1,05 |
1,0 |
||||
|
Нижнее, горизонтальное, вертикальное |
βf |
0,9 |
0,8 |
0,7 |
||
|
βz |
1,05 |
1,0 |
||||
|
Ручная, механизированная проволокой сплошного сечения при d < 1,4 или порошковой проволокой |
В лодочку |
βf |
0,7 |
|||
|
Нижнее, горизонтальное, вертикальное, потолочное |
βz |
1,0 |
||||
15.1.8 Для угловых швов, размеры которых установлены в соответствии с расчетом, для элементов из стали с пределом текучести до 285 Н/мм2 следует, как правило, применять электродные материалы, удовлетворяющие условиям: Rwf > Rwz при механизированной сварке и 1,1Rwz ≤ Rwf ≤ Rwzβz/βf при ручной сварке, а для элементов из стали с пределом текучести свыше 285 Н/мм2 допускается применять электродные материалы, удовлетворяющие условию Rwz < Rwf < Rwzβz/βf (здесь βf и βz - коэффициенты, зависящие от технологии сварки и катета шва и определяемые по таблице 36).
15.1.9 Односторонние угловые швы в тавровых соединениях элементов из стали с пределом текучести до 375 Н/мм2, как правило, применяют в конструкциях, эксплуатируемых в неагрессивной или слабоагрессивной среде (классификация по СНиП 2.03.11) в отапливаемых помещениях, кроме конструкций в зданиях и сооружениях, относящихся к I уровню ответственности, возводимых в районах с сейсмичностью 8 баллов и выше, в районах с расчетной температурой ниже минус 45 °С, а также конструкций групп 1, 2, 3 в зданиях с кранами режимов работы 7К (в цехах металлургических производств) и 8К:
для прикрепления промежуточных ребер жесткости и диафрагм - в конструкциях всех групп, кроме конструкций группы 1, рассчитываемых на усталость;
для поясных швов сварных двутавров - в конструкциях групп 2 и 3, кроме балок с
условной гибкостью стенки ![]() , при толщине стенки tw в колоннах и стойках
до 12 мм и в балках до 10 мм,
при выполнении швов механизированной сваркой с катетом шва kf ≥ 0,8tw/βf и с учетом требований 16.3.3 и 16.5.5;
, при толщине стенки tw в колоннах и стойках
до 12 мм и в балках до 10 мм,
при выполнении швов механизированной сваркой с катетом шва kf ≥ 0,8tw/βf и с учетом требований 16.3.3 и 16.5.5;
для всех конструктивных элементов - в конструкциях группы 4.
Односторонние угловые швы не применяют в соединениях, воспринимающих изгибающие моменты относительно продольной оси шва.
Катеты односторонних швов принимают по расчету, но не менее указанных в таблице 35.
15.1.10 Прерывистые угловые сварные швы допускается применять при статической нагрузке при избыточной несущей способности непрерывного шва минимального размера для соединений в конструкциях группы 4, а также в конструкциях группы 3, реконструируемых в районах, кроме имеющих расчетную температуру ниже минус 45 °С, и эксплуатируемых в неагрессивных или слабоагрессивных средах.
Размеры сварного шва должны соответствовать требованиям 15.1.7.
Расстояние s между участками сварных швов (рисунок 17), как правило, не должно превышать одного из значений: 200 мм, 12tmin в сжатом элементе (tmin - толщина самого тонкого из соединяемых элементов), 16tmin в растянутом элементе. В конструкциях группы 4 расстояние s допускается увеличить на 50 %.
а - в нахлесточном соединении; б - в тавровом соединении
Рисунок 17 - Схема прерывистых угловых сварных швов
При наложении прерывистого шва предусматривают шов по концам соединяемых частей элементов; длина lw1 этого шва в элементах составного сечения из пластин должна быть не менее 0,75b, где b - ширина более узкой из соединяемых пластин.
15.1.11 Угловые сварные швы, расположенные по периметру отверстий или прорезей, допускается применять в нахлесточных соединениях в случаях, предусмотренных 15.1.10, для передачи усилий в плоскости нахлестки, предотвращения потери устойчивости элементов нахлестки или конструктивных соединений элементов.
15.1.12 Пробочные швы, заполняющие наплавленным металлом всю площадь круглых или щелевых отверстий, допускается применять в нахлесточных соединениях в случаях, предусмотренных 15.1.10, только для предотвращения потери устойчивости элементов нахлестки или для конструктивных соединений элементов.
Толщина пробочного шва должна быть: не менее толщины t просверленного или прорезанного элемента, но не более 16 мм, не менее 0,1 длины прорези либо значений 0,45d или 0,45b (где d и b - диаметр отверстия и ширина прорези, равные d ≥ t + 8 мм и b ≥ t + 8 мм).
Расстояние между центрами отверстий или продольными осями прорезей должно быть не менее 4d или 4b.
15.1.13 Применение комбинированных соединений, в которых часть сдвигающего усилия воспринимается фрикционным соединением, а часть - сварными швами, допускается при условии, что сварка должна быть выполнена после окончательной затяжки болтов.
Распределение усилия между фрикционными и сварными соединениями допускается принимать пропорционально их несущим способностям либо принимать, что фрикционное соединение воспринимает усилие от постоянной нагрузки, а сварное - от временной. Применение других болтовых соединений в комбинированных соединениях не допускается.
15.1.14 Расчет сварных стыковых соединений при действии осевой силы N, проходящей через центр тяжести соединения, выполняют по формуле
N/(tlwRwyγc) ≤ 1, (154)
где t - наименьшая из толщин соединяемых элементов;
lw - расчетная длина шва, равная полной его длине, уменьшенной на 2t, или полной его длине, если концы шва выведены за пределы стыка.
При расчете сварных стыковых соединений элементов из стали с отношением Ru/γu > Ry, эксплуатация которых возможна и после достижения металлом предела текучести, а также из стали с пределом текучести Ryn > 440 Н/мм2 в формуле (154) вместо Rwy принимают Rwu/γu.
Расчет сварных стыковых соединений выполнять не требуется при применении сварочных материалов согласно приложению Г, полном проваре соединяемых элементов и физическом контроле качества соединений при растяжении.
15.1.15 Сварные стыковые соединения, выполненные без физического контроля качества, при одновременном действии в одном и том же сечении шва нормальных σwx и σwy и касательных τwxy напряжений проверяют по формуле (38), принимая в ней:
σx = σwx, σy = σwy, τxy = τwxy, Ry = Rwy.
15.1.16 Расчет сварного соединения с угловыми швами, при действии силы N, проходящей через центр тяжести соединения, выполняют на срез (условный) по одному из двух сечений (рисунок 18) по формулам:
при ![]()
по металлу шва
![]() (155)
(155)
при ![]()
по металлу границы сплавления
![]() (156)
(156)
где lw - расчетная длина швов в сварном соединении, равная суммарной длине всех его участков за вычетом по 1 см на каждом непрерывном участке шва;
βf, βz - коэффициенты, принимаемые по таблице 36.
1 - по металлу шва; 2 - по металлу границы сплавления
Рисунок 18 - Схемы расчетных сечений сварного соединения с угловым швом
15.1.17 Расчет сварных соединений с угловыми швами при действии момента M в плоскости, перпендикулярной плоскости расположения швов, выполняют на срез (условный) по одному из двух сечений (рисунок 18) по формулам:
по металлу шва
![]() (157)
(157)
по металлу границы сплавления
![]() (158)
(158)
где Wf и Wz - моменты сопротивления расчетных сечений сварного соединения по металлу шва и по металлу границы сплавления соответственно.
15.1.18 Расчет сварного соединения с угловыми швами при действии момента M в плоскости расположения этих швов выполняют на срез (условный) по одному из двух сечений (рисунок 18) по формулам:
по металлу шва
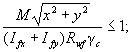 (159)
(159)
по металлу границы сплавления
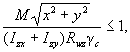 (160)
(160)
где x и y - координаты точки сварного соединения, наиболее удаленной от центра тяжести О расчетного сечения этого соединения (рисунок 19);
Ifx, Ify - моменты инерции расчетного сечения сварного соединения по металлу шва относительно его главных осей x-x и у-у;
Izx, Izy - то же, по металлу границы сплавления.
Рисунок 19 - Расчетная схема сварного соединения
15.1.19 При расчете сварного соединения с угловыми швами на одновременное действие продольной N поперечной V сил и момента M (рисунок 19) должны быть выполнены условия:
τf/(Rwfγc) ≤ 1 и τz/(Rwzγc) ≤ 1, (161)
где τf и τz - напряжения в точке расчетного сечения сварного соединения по металлу шва и по металлу границы сплавления соответственно, определяемые по формуле
![]() (162)
(162)
15.1.20 Нахлесточные соединения элементов толщиной до 4 мм допускается осуществлять точечным швом дуговой сваркой сквозным проплавлением; при этом несущую способность одной точки принимают равной меньшему из двух предельных значений:
при срезе
Ns = 0,28d2Rwun; (163)
при вырыве
Nt = βdtRun, (164)
где d - диаметр точечного шва в плоскости соединяемых элементов, принимаемый по ГОСТ 14776; при применении способа сварки, не предусмотренного ГОСТ 14776, значение d следует согласовывать и принимать в установленном порядке;
β = 1,1 при сварке элементов равной толщины;
β = 1,9 при сварке элементов с разными толщинами, отличающимися в два и более раза (при меньшем отличии в толщинах значение β принимают по интерполяции);
t - меньшая из толщин свариваемых элементов.
15.2 БОЛТОВЫЕ СОЕДИНЕНИЯ
15.2.1 Для болтовых соединений элементов стальных конструкций применяют болты согласно приложению Г.
15.2.2 Болты размещают согласно требованиям таблицы 37, при этом в стыках и в узлах на минимальных расстояниях, а соединительные конструктивные болты, как правило, на максимальных расстояниях.
При прикреплении уголка одной полкой болтами, размещаемыми в шахматном порядке, отверстие, наиболее удаленное от его конца, размещают на риске, ближайшей к обушку.
Допускается крепить элементы одним болтом.
15.2.3 Болты класса точности А применяют для соединений, в которых отверстия просверлены на проектный диаметр в собранных элементах либо по кондукторам в отдельных элементах и деталях, либо просверлены или продавлены на меньший диаметр в отдельных деталях с последующей рассверловкой до проектного диаметра в собранных элементах.
Таблица 37
|
№ п.п. |
Характеристика расстояния и предела текучести соединяемых элементов |
Расстояние при размещении болтов |
|
1 |
Расстояние между центрами отверстий для болтов в любом направлении: |
|
|
минимальное: |
||
|
при Ryn ≤ 375 Н/мм2 |
От 2d до 2,5d |
|
|
при Ryn > 375 Н/мм2 |
3d |
|
|
максимальное в крайних рядах при отсутствии окаймляющих уголков при растяжении и сжатии |
8d или 12t |
|
|
максимальное в средних рядах, а также в крайних рядах при наличии окаймляющих уголков: |
|
|
|
при растяжении |
16d или 24t |
|
|
при сжатии |
12d или 18t |
|
|
2 |
Расстояние от центра отверстия для болта до края элемента |
|
|
минимальное вдоль усилия: |
||
|
при Rvn ≤ 375 Н/мм2 |
От 1,5d до 2d |
|
|
при Rvn > 375 Н/мм2 |
2,5d |
|
|
то же, поперек усилия: |
|
|
|
при обрезных кромках |
1,5d |
|
|
при прокатных кромках |
1,2d |
|
|
максимальное |
4d или 8t |
|
|
минимальное во фрикционном соединении при любой кромке и любом направлении усилия |
1,3d |
|
|
3 |
Расстояние, максимальное между центрами отверстий вдоль усилия для болтов, размещаемых в шахматном порядке |
u + 1,5d |
|
Обозначения, принятые в таблице 37: d - диаметр отверстия для болта; t - толщина наиболее тонкого наружного элемента; u - расстояние поперек усилия между рядами отверстий. Примечания 1 Диаметр отверстий принимают: для болтов класса точности А d = db; для болтов классов точности В и С в конструкциях опор ВЛ, ОРУ и КС d = db + 1 мм, в остальных случаях - d = db + 3 мм. 2 В одноболтовых соединениях элементов решетки (раскосов и распорок), кроме постоянно работающих на растяжение, при толщине элемента до 6 мм из стали с пределом текучести до 375 Н/мм2 расстояние от края элемента до центра отверстия вдоль усилия допускается принимать 1,35d без допуска в сторону уменьшения при изготовлении элементов, о чем должно быть указано в проекте. 3 При размещении болтов в шахматном порядке на расстоянии, не менее указанного в позиции 3, сечение элемента An определяют с учетом ослабления его отверстиями, расположенными в одном сечении поперек усилия (не по зигзагу). |
||
Болты классов точности В и С в многоболтовых соединениях применяют для конструкций из стали с пределом текучести до 375 Н/мм2.
В соединениях, где болты работают преимущественно на растяжение, как правило, применяют болты классов точности В и С или высокопрочные.
15.2.4 Болты, имеющие по длине ненарезанной части участки с различными диаметрами, не применяют в соединениях, в которых эти болты работают на срез.
15.2.5 Резьба болта, воспринимающего сдвигающее усилие, в элементах структурных конструкций, опор линий электропередачи и открытых распределительных устройств, а также в соединениях при толщине наружного элемента до 8 мм должна находиться вне пакета соединяемых элементов; в остальных случаях резьба болта не должна входить вглубь отверстия более чем на половину толщины крайнего элемента со стороны гайки или свыше 5 мм.
15.2.6 Установку шайб на болты выполняют согласно требованиям СНиП 3.03.01.
В расчетных соединениях с болтами классов точности А, В, С (за исключением крепления вспомогательных конструкций) предусматривают меры против самоотвинчивания гаек (постановка пружинных шайб, вторых гаек и др.).
15.2.7 На скошенных поверхностях соединяемых деталей и элементов (внутренние грани полок двутавров и швеллеров) под головки болтов и гайки дополнительно устанавливают косые шайбы.
15.2.8 Диаметр отверстия для болтов в элементах из проката должен соответствовать ГОСТ 24839.
15.2.9 Расчетное усилие, которое может быть воспринято одним болтом, в зависимости от вида напряженного состояния определяют по формулам:
при срезе
Nbs = RbsAbnsγbγc; (165)
при смятии
Nbp = RbpdpΣtγbγc; (166)
при растяжении
Nbt = RbtAbnγc, (167)
где Rbs, Rbp, Rbt - расчетные сопротивления одноболтовых соединений;
Ab и Abn - площади сечения стержня болта и нетто болта по резьбе соответственно, принимаемые согласно таблице Г.8 приложения Г;
ns - число расчетных срезов одного болта;
db - наружный диаметр стержня болта;
Σt - наименьшая суммарная толщина соединяемых элементов, сминаемых в одном направлении;
γc - коэффициент условий работы, определяемый по таблице 1;
γb - коэффициент условий работы болтового соединения, определяемый по таблице 38.
Таблица 38
|
Предел текучести Ryn стали соединяемых элементов, Н/мм2 |
Значения a/d, s/d |
Значение коэффициента γb |
||
|
болтового соединения |
напряженного состояния |
|||
|
Одноболтовое, болт классов точности А, В, С или высокопрочный |
Срез |
- |
- |
1,0 |
|
Смятие |
До 285 |
1,5 ≤ a/d ≤ 2; |
0,4a/d + 0,2; |
|
|
1,35 ≤ a/d < 1,5 |
a/d - 0,7 |
|||
|
Св. 285 до 375 |
1,5 ≤ a/d ≤ 2; |
0,5a/d; |
||
|
1,35 ≤ a/d ≤ 5 |
0,67a/d - 0,25 |
|||
|
Св. 375 |
a/d ≥ 2,5 |
1,0 |
||
|
Многоболтовое, болты класса точности А |
Срез |
- |
- |
1,0 |
|
Смятие |
До 285 |
1,5 ≤ a/d ≤ 2; |
0,4a/d + 0,2; |
|
|
2 ≤ s/d ≤ 2,5 |
0,4s/d |
|||
|
Св. 285 до 375 |
1,5 ≤ a/d ≤ 2; |
0,5a/d; |
||
|
2 ≤ s/d ≤ 2,5 |
0,5s/d - 0,25 |
|||
|
Св. 375 |
a/d ≥ 2,5; |
1,0 |
||
|
s/d ≥ 3 |
1,0 |
|||
|
Обозначения, принятые в таблице 38: a - расстояние вдоль усилия от края элемента до центра ближайшего отверстия; s - расстояние вдоль усилия между центрами отверстий; d - диаметр отверстия для болта. Примечания 1 Для расчета многоболтового соединения на срез и смятие при болтах классов точности В, С, а также при высокопрочных болтах с нерегулируемым натяжением при всех значениях предела текучести Ryn стали соединяемых элементов значения коэффициента γb умножают на 0,9. 2 Для расчета многоболтового соединения на смятие принимают значение γb, меньшее из вычисленных при принятых значениях d, a, s. |
||||
15.2.10 При действии на болтовое соединение силы N, проходящей через центр тяжести соединения, принимают, что эта сила распределяется между болтами равномерно. В этом случае количество болтов в соединении определяют по формуле
n ≥ N/Nb,min, (168)
где Nb,min - наименьшее из значений Nbs или Nbp либо значение Nbt, вычисленное согласно требованиям 15.2.9.
В случаях когда в стыке расстояние l между крайними болтами вдоль сдвигающего усилия превышает 16d, значение n в формуле (168) увеличивают путем деления на коэффициент β = 1 - 0,005(l/d - 16), принимаемый равным не менее 0,75. Это требование не распространяется при действии усилия по всей длине соединения (например, в поясном соединении балки).
15.2.11 При действии на болтовое соединение момента, вызывающего сдвиг соединяемых элементов, принимают, что усилия распределяются между болтами пропорционально расстояниям от центра тяжести соединения до рассматриваемого болта.
Усилие в наиболее нагруженном болте Nb,max не должно превышать меньшего из значений Nbs или Nbp, вычисленных согласно требованиям 15.2.9.
15.2.12 При одновременном действии на болтовое соединение силы и момента, действующих в одной плоскости и вызывающих сдвиг соединяемых элементов, определяют равнодействующее усилие в наиболее нагруженном болте, которое не должно превышать меньшего из значений Nbs или Nbp, вычисленных согласно требованиям 15.2.9.
15.2.13 При одновременном действии на болтовое соединение усилий, вызывающих срез и растяжение болтов, наиболее напряженный болт наряду с проверкой по формуле (167) проверяют по формуле
![]() (169)
(169)
где Ns и Nt - усилия, действующие на болт, срезывающее и растягивающее соответственно;
Nbs, Nbt - расчетные усилия, определяемые согласно требованиям 15.2.9, с заменой значения Abn на Ab.
15.2.14 В креплениях одного элемента к другому через прокладки или иные промежуточные элементы, а также в элементах с односторонней накладкой количество болтов по сравнению с расчетом увеличивают на 10 %.
При креплениях выступающих полок уголков или швеллеров с помощью коротышей количество болтов, прикрепляющих коротыш к этой полке, по сравнению с расчетом увеличивают на 50 %.
15.2.15 Фундаментные (анкерные) болты проверяют согласно требованиям СНиП 2.09.03.
15.3 ФРИКЦИОННЫЕ СОЕДИНЕНИЯ (НА БОЛТАХ С КОНТРОЛИРУЕМЫМ НАТЯЖЕНИЕМ)
15.3.1 Фрикционные соединения, в которых усилия передаются через трение, возникающее по соприкасающимся поверхностям соединяемых элементов вследствие натяжения высокопрочных болтов, применяют:
в конструкциях, непосредственно воспринимающих подвижные, вибрационные и другие динамические нагрузки;
в многоболтовых соединениях, к которым предъявляются повышенные требования в отношении ограничения деформативности.
15.3.2 Во фрикционных соединениях применяют болты, гайки и шайбы согласно требованиям 6.8.
Болты размещают согласно требованиям таблицы 37.
15.3.3 Расчетное усилие, которое может быть воспринято каждой плоскостью трения элементов, стянутых одним высокопрочным болтом, определяют по формуле
Qbh = RbhAbnμ/γh, (170)
где Rbh - расчетное сопротивление растяжению высокопрочного болта, определяемое согласно требованиям 7.7;
Abn - площадь сечения болта по резьбе, принимаемая согласно таблице Г.9 приложения Г;
μ - коэффициент трения, принимаемый по таблице 39;
γh - коэффициент надежности, принимаемый по таблице 39.
15.3.4 При действии на фрикционное соединение силы N, вызывающей сдвиг соединяемых элементов и проходящей через центр тяжести соединения, принимают, что эта сила распределяется между болтами равномерно. В этом случае количество болтов в соединении определяют по формуле
n ≥ N/(Qbhкγbγc), (171)
где Qbh - расчетное усилие, определяемое по формуле (170);
к - количество плоскостей трения соединяемых элементов;
Таблица 39
|
№ п.п. |
Способ обработки (очистки) соединяемых поверхностей |
Коэффициент трения μ |
Коэффициент γh при контроле натяжения болтов по моменту закручивания при нагрузке и при разности номинальных диаметров отверстий и болтов δ, мм |
|
|
динамической δ = 3 ÷ 6; статической δ = 5 ÷ 6 |
динамической δ = 1; статической δ = 1 ÷ 4 |
|||
|
1 |
Дробеметный или дробеструйный двух поверхностей без консервации |
0,58 |
1,35 |
1,12 |
|
2 |
Газопламенный двух поверхностей без консервации |
0,42 |
1,35 |
1,12 |
|
3 |
Стальными щетками двух поверхностей без консервации |
0,35 |
1,35 |
1,17 |
|
4 |
Без обработки |
0,25 |
1,70 |
1,30 |
|
Примечание - При контроле натяжения болтов по углу поворота гайки значения γh умножают на 0,9. |
||||
γc - коэффициент условий работы, принимаемый по таблице 1;
γb - коэффициент условий работы фрикционного соединения, зависящий от количества n болтов, необходимых для восприятия расчетного усилия, и принимаемый равным:
0,8 при n < 5;
0,9 при 5 ≤ n < 10;
1,0 при n ≥ 10.
15.3.5 При действии на фрикционное соединение момента или силы и момента, вызывающих сдвиг соединяемых элементов, распределение усилий между болтами принимают согласно указаниям 15.2.11 и 15.2.12.
15.3.6 При действии на фрикционное соединение помимо силы N, вызывающей сдвиг соединяемых элементов, силы F, вызывающей растяжение в болтах, значение коэффициента γb, определяемое согласно требованиям 15.3.4, умножают на коэффициент (1 - Nt/Pb), где Nt - растягивающее усилие, приходящееся на один болт, Pb - усилие натяжения болта, принимаемое равным Pb = RbhAbh.
15.3.7 Диаметр болта во фрикционном соединении принимают не менее толщины наиболее толстого из соединяемых элементов.
Во фрикционных соединениях с большим количеством болтов их диаметр назначают возможно большим.
15.3.8 В проекте должны быть указаны марки стали и механические свойства болтов, гаек и шайб и стандарты, по которым они должны поставляться, способ обработки соединяемых поверхностей, осевое усилие Pb, принимаемое согласно 15.3.6.
15.3.9 При проектировании фрикционных соединений обеспечивают свободный доступ для установки болтов, плотного стягивания пакета болтами и закручивания гаек с применением динамометрических ключей, гайковертов и др.
15.3.10 Для высокопрочных болтов по ГОСТ 22353 с увеличенными размерами головок и гаек и при разности номинальных диаметров отверстия и болта не более 3 мм, а в конструкциях из стали с временным сопротивлением не ниже 440 Н/мм2 - не более 4 мм допускается установка одной шайбы под гайку.
15.3.11 Расчет на прочность соединяемых элементов, ослабленных отверстиями во фрикционном соединении, выполняют с учетом того, что половина усилия, приходящегося на каждый болт, передана силами трения. При этом проверку ослабленных сечений выполняют: при подвижных, вибрационных и других динамических нагрузках по площади сечения нетто An; при статических нагрузках по площади сечения брутто A при An ≥ 0,85A либо по условной площади Aef = 1,18An при An < 0,85A.
15.4 ПОЯСНЫЕ СОЕДИНЕНИЯ В СОСТАВНЫХ БАЛКАХ
15.4.1 Сварные и фрикционные поясные соединения составной двутавровой балки рассчитывают по формулам таблицы 40.
При отсутствии поперечных ребер жесткости для передачи неподвижных сосредоточенных нагрузок, приложенных к верхнему поясу, а также при приложении неподвижной сосредоточенной нагрузки к нижнему поясу независимо от наличия ребер жесткости в местах приложения нагрузки поясные соединения рассчитывают как для подвижной нагрузки.
Таблица 40
|
Поясные соединения |
Формулы для расчета поясных соединений в составных балках |
|
|
Неподвижная |
Сварные |
T/(nβfkfRwfγc) ≤ 1; (172) T/(nβzkfRwzγc) ≤ 1 (173) |
|
Фрикционные |
Ts/(Qbhkγc) ≤ 1 (174) |
|
|
Подвижная |
Сварные (двусторонние швы) |
|
|
Фрикционные |
|
|
|
Обозначения, принятые в таблице 40: T = QS/I - сдвигающее пояс усилие на единицу длины, вызываемое поперечной силой Q (здесь S - статический момент брутто пояса балки относительно центральной оси); n - количество угловых швов: при двусторонних швах n = 2, при односторонних n = 1; Qbh, k - величины, определяемые согласно 15.3.3, 15.3.4; V = γfγf1Fn/lef - давление от сосредоточенного груза Fn на единицу длины, определяемое с учетом требований 9.2.2 и 9.3.3 (для неподвижных грузов γf1 = 1); γf и γf1 - коэффициенты надежности по нагрузке, принимаемые по СНиП 2.01.07; s - шаг поясных болтов; α - коэффициент, принимаемый равным: α = 0,4 при нагрузке по верхнему поясу балки, к которому пристрогана стенка, и α = 1,0 при отсутствии пристрожки стенки или при нагрузке по нижнему поясу. |
||
Сварные швы, выполненные с проваром на всю толщину стенки, считают равнопрочными со стенкой.
15.4.2 В балках с фрикционными поясными соединениями с многолистовыми поясными пакетами прикрепление каждого из листов за местом своего теоретического обрыва рассчитывают на половину усилия, которое может быть воспринято сечением листа. Прикрепление каждого листа на участке между действительным местом его обрыва и местом обрыва предыдущего листа рассчитывают на полное усилие, которое может быть воспринято сечением листа.
16 ДОПОЛНИТЕЛЬНЫЕ ТРЕБОВАНИЯ ПО ПРОЕКТИРОВАНИЮ НЕКОТОРЫХ ВИДОВ ЗДАНИЙ, СООРУЖЕНИЙ И КОНСТРУКЦИЙ
16.1 РАССТОЯНИЯ МЕЖДУ ТЕМПЕРАТУРНЫМИ ШВАМИ
16.1.1 Расстояния l между температурными швами стальных каркасов одноэтажных зданий и сооружений, как правило, не должны превышать наибольших значений lu, принимаемых по таблице 41.
Таблица 41
|
Наибольшее расстояние lu, м, между температурными швами для районов со средней месячной температурой воздуха, °С, в январе1 |
|||||
|
здания и сооружения |
направления |
От +5 до 0 |
От -5 до -10 |
От -15 до -30 |
От -35 до -50 |
|
Отапливаемое здание |
Вдоль блока |
350 |
280 |
230 |
160 |
|
Поперек блока |
230 |
180 |
150 |
110 |
|
|
Неотапливаемое здание |
Вдоль блока |
300 |
240 |
200 |
140 |
|
Поперек блока |
180 |
150 |
120 |
90 |
|
|
Горячий цех |
Вдоль блока |
230 |
180 |
150 |
110 |
|
Поперек блока |
140 |
120 |
100 |
75 |
|
|
Открытая эстакада |
Вдоль блока |
180 |
150 |
130 |
100 |
|
1 Районирование принимают по карте 5 приложения 5 к СНиП 2.01.07. |
|||||
16.1.2 Значения расстояний, указанные в таблице 41 для зданий с высотой колонн h1 или h2 свыше 12 м, допускается увеличивать, умножая на коэффициент, принимаемый равным:
вдоль блока k1 = h1/hn ≤ 1,5;
поперек блока k2 = h2/hn ≤ 1,5,
где h1 - высота, м, колонн в плоскости продольных конструкций каркаса (вдоль блока), равная расстоянию от верха фундамента до низа подкрановой балки (при двухъярусном расположении кранов - до низа подкрановой балки нижнего яруса) или до уровня опирания несущей конструкции покрытия (в зданиях без мостовых кранов);
hn - 12 м;
h2 - высота, м, крайней колонны в плоскости поперечной конструкции каркаса (поперек блока), равная расстоянию от верха фундамента до уровня опирания несущей конструкции покрытия.
16.1.3 Вертикальные связи, установленные между колоннами в пределах высоты h1 вдоль температурного блока, должны удовлетворять следующим требованиям:
расстояние от торца блока до оси ближайшей связи не должно превышать 0,5luk1;
расстояние между осями крайних связей при их установке в нескольких местах не должно превышать 0,3luk1 (здесь luk1 - наибольшая длина блока согласно требованиям 16.1.1 и 16.1.2).
16.1.4 Наибольшие расстояния lu, устанавливаемые согласно требованиям 16.1.1 и 16.1.2, допускается увеличивать на основе расчета с учетом влияния стен или других ограждающих конструкций, климатических температурных воздействий, неупругих деформаций конструкций и податливости узлов.
16.2 ФЕРМЫ И СТРУКТУРНЫЕ ПЛИТЫ ПОКРЫТИЙ
16.2.1 Оси стержней ферм и структур должны быть, как правило, центрированы во всех узлах. Центрирование стержней следует производить в сварных фермах по центрам тяжести сечений (с округлением до 5 мм), а в болтовых - по рискам уголков, ближайшим к обушку.
Смещение осей поясов ферм при изменении сечений допускается не учитывать, если оно не превышает 1,5 % высоты пояса меньшего сечения.
При наличии эксцентриситетов в узлах элементы ферм и структур рассчитывают с учетом соответствующих изгибающих моментов.
При приложении нагрузок вне узлов ферм пояса рассчитывают на совместное действие продольных усилий и изгибающих моментов.
16.2.2 При расчете плоских ферм соединения элементов в узлах ферм допускается принимать шарнирными:
при сечениях элементов из уголков или тавров;
при двутавровых, Н-образных и трубчатых сечениях элементов, когда отношение высоты сечения h к длине элемента l между узлами не превышает: 1/15 - для конструкций, эксплуатируемых в районах с расчетными температурами ниже минус 45 °С; 1/10 - для конструкций, эксплуатируемых в остальных районах.
При превышении указанных отношений h/l учитывают дополнительные изгибающие моменты в элементах от жесткости узлов; при этом допускается определять осевые усилия по шарнирной схеме.
16.2.3 Расстояние между краями элементов решетки и пояса в узлах сварных ферм с фасонками принимают не менее a = (6t - 20) мм, но не более 80 мм (здесь t - толщина фасонки, мм).
Между торцами стыкуемых элементов поясов ферм, перекрываемых накладками, оставляют зазор не менее 50 мм.
Сварные швы, прикрепляющие элементы решетки ферм к фасонкам, выводят на торец элемента на длину 20 мм.
16.2.4 В узлах ферм с поясами из тавров, двутавров и одиночных уголков крепления фасонок к полкам поясов встык осуществляют с проваром на всю толщину фасонки. В конструкциях группы 1, а также эксплуатируемых в районах при расчетных температурах ниже минус 45 °С примыкание узловых фасонок к поясам выполняют согласно приложению Р (таблица Р.1, позиция 7).
16.2.5 При расчете узлов ферм со стержнями трубчатого и двутаврового сечений и прикреплением элементов решетки непосредственно к поясу (без фасонок) проверяют несущую способность:
стенки пояса при местном изгибе (продавливании) в местах примыкания элементов решетки (для круглых и прямоугольных труб);
боковой стенки пояса в месте примыкания сжатого элемента решетки (для прямоугольных труб);
полок пояса на отгиб (для двутаврового сечения);
стенки пояса (для двутаврового сечения);
элементов решетки в сечении, примыкающем к поясу;
сварных швов, прикрепляющих элементы решетки к поясу.
Указанные проверки приведены в приложении С.
16.2.6 При пролетах ферм покрытий свыше 36 м предусматривают строительный подъем, равный прогибу от постоянной и длительной нагрузок. При плоских кровлях строительный подъем предусматривают независимо от величины пролета, принимая его равным прогибу от суммарной нормативной нагрузки плюс 1/200 пролета.
16.3 КОЛОННЫ
16.3.1 Отправочные элементы сквозных колонн с решетками в двух плоскостях укрепляют диафрагмами, располагаемыми у концов отправочного элемента.
В сквозных колоннах с соединительной решеткой в одной плоскости диафрагмы располагают не реже, чем через 4 м.
16.3.2 В колоннах и стойках с односторонними поясными швами согласно 15.1.9 в узлах крепления связей, балок, распорок и других элементов в зоне передачи усилия применяют двусторонние поясные швы, выходящие за контуры прикрепляемого элемента (узла) на длину 30kf с каждой стороны.
16.3.3 Угловые швы, прикрепляющие фасонки соединительной решетки к колоннам внахлестку, назначают по расчету и располагают с двух сторон фасонки вдоль колонн в виде отдельных участков в шахматном порядке; при этом расстояние между концами таких швов не должно превышать 15 толщин фасонки.
В конструкциях, возводимых в районах с расчетными температурами ниже минус 45 °С, а также при применении ручной дуговой сварки швы должны быть непрерывными по всей длине фасонки.
16.3.4 Монтажные стыки колонн выполняют с фрезерованными торцами, сваренными встык, на накладках со сварными швами или болтовыми соединениями, в том числе фрикционными. При приварке накладок швы не доводят до стыка на 25 мм с каждой стороны. Допускается применение фланцевых соединений с передачей сжимающих усилий через плотное касание, а растягивающих - болтами.
16.3.5 В сквозных колоннах, ветви которых соединены планками, принимают:
ширину bs промежуточных планок - равной от 0,5b до 0,75b (здесь b - габаритная ширина колонны в плоскости планок);
ширину концевых планок - равной от 1,3bs до 1,7bs.
16.4 СВЯЗИ
16.4.1 В каждом температурном блоке здания предусматривают самостоятельную систему связей.
16.4.2 Нижние пояса балок и ферм крановых путей пролетом свыше 12 м укрепляют горизонтальными связями.
16.4.3 Вертикальные связи между основными колоннами ниже уровня балок крановых путей при двухветвевых колоннах располагают в плоскости каждой из ветвей колонны.
Ветви двухветвевых связей, как правило, соединяют между собой соединительными решетками.
16.4.4 Поперечные горизонтальные связи предусматривают в уровне верхнего или нижнего пояса стропильных ферм в каждом пролете здания по торцам температурных блоков. При длине температурного блока более 144 м предусматривают промежуточные поперечные горизонтальные связи.
Стропильные фермы, не примыкающие непосредственно к поперечным связям, раскрепляют в плоскости расположения этих связей распорками и растяжками.
В местах расположения поперечных связей предусматривают вертикальные связи между фермами.
При наличии жесткого диска кровли в уровне верхних поясов предусматривают инвентарные съемные связи для выверки конструкций и обеспечения их устойчивости в процессе монтажа.
В покрытиях зданий и сооружений, эксплуатируемых в районах с расчетными температурами ниже минус 45 °С, как правило, предусматривают (дополнительно к обычно применяемым) вертикальные связи посередине каждого пролета вдоль всего здания.
16.4.5 Продольные горизонтальные связи в плоскости нижних поясов стропильных ферм предусматривают: вдоль крайних рядов колонн в зданиях с кранами групп режимов работы 6К - 8К по ГОСТ 25546; в покрытиях с подстропильными фермами; в одно- и двухпролетных зданиях с мостовыми кранами грузоподъемностью 10 т и более, а при отметке низа стропильных конструкций свыше 18 м - независимо от грузоподъемности кранов.
В зданиях с числом пролетов более трех горизонтальные продольные связи размещают также вдоль средних рядов колонн не реже, чем через пролет в зданиях с кранами групп режимов работы 6К - 8К по ГОСТ 25546 и через два пролета - в прочих зданиях.
16.4.6 Горизонтальные связи по верхним и нижним поясам разрезных ферм пролетных строений транспортерных галерей конструируют раздельно для каждого пролета.
16.4.7 При применении крестовой решетки связей покрытий, за исключением зданий и сооружений I уровня ответственности, допускается расчет по условной схеме в предположении, что раскосы воспринимают только растягивающие усилия.
При определении усилий в элементах связей обжатие поясов ферм, как правило, не учитывают.
16.4.8 В висячих покрытиях с плоскостными несущими системами (двухпоясными, изгибно-жесткими вантами и т.п.) предусматривают вертикальные и горизонтальные связи между несущими системами.
16.5 БАЛКИ
16.5.1 Пакеты листов для поясов сварных двутавровых балок, как правило, не применяют.
Для поясов балок с фрикционными соединениями допускается применять пакеты, состоящие не более чем из трех листов; при этом площадь сечения поясных уголков принимают равной не менее 30 % всей площади сечения пояса.
16.5.2 Поясные швы сварных балок, а также швы, присоединяющие к основному сечению балки вспомогательные элементы (например, ребра жесткости), как правило, выполняют непрерывными. Поперечные ребра жесткости должны иметь вырезы для пропуска поясных швов.
16.5.3 При применении односторонних поясных швов в сварных двутавровых балках 1-го класса, несущих статическую нагрузку, выполняют следующие требования:
расчетная нагрузка должна быть приложена симметрично относительно поперечного сечения балки;
должна быть обеспечена устойчивость сжатого пояса балки в соответствии с 9.4.4, а;
в местах приложения к поясу балки сосредоточенных нагрузок, включая нагрузки от ребристых железобетонных плит, должны быть установлены поперечные ребра жесткости.
В ригелях рамных конструкций у опорных узлов, а также в местах, где нагрузка вызывает изгиб в плоскости, перпендикулярной продольной оси сварного шва, применяют двусторонние поясные швы.
В балках с сечениями 2-го и 3-го классов, а также с условной гибкостью стенки ![]() применение
односторонних поясных швов не допускается.
применение
односторонних поясных швов не допускается.
16.5.4. Ребра жесткости сварных балок должны быть удалены от стыков стенки на расстояние не менее 10 толщин стенки. В местах пересечения стыковых швов стенки балки с продольным ребром жесткости швы, прикрепляющие продольное ребро жесткости к стенке, не доводят до стыкового шва стенки в местах их пересечения на (6t - 20) мм.
16.5.5 В сварных двутавровых балках конструкций групп 2 - 4 следует, как правило, применять односторонние ребра жесткости с расположением их с одной стороны балки и приваркой их к поясам балки.
В балках с односторонними поясными швами ребра жесткости располагают со стороны стенки, противоположной расположению односторонних поясных швов.
16.6 БАЛКИ КРАНОВЫХ ПУТЕЙ
16.6.1 Верхние поясные швы в балках крановых путей для кранов групп режимов работы 7К (в цехах металлургических производств) и 8К по ГОСТ 25546 выполняют с проваром на всю толщину стенки.
16.6.2 Свободные кромки растянутых поясов балок крановых путей и балок рабочих площадок, непосредственно воспринимающих нагрузку от подвижных составов, должны быть прокатными, строгаными или обрезанными машинной кислородной или плазменно-дуговой резкой.
16.6.3 Размеры ребер жесткости балок крановых путей должны удовлетворять требованиям 9.5.9, 9.5.10 и 9.5.13, при этом ширина выступающей части двустороннего промежуточного ребра должна быть не менее 90 мм. Двусторонние поперечные ребра жесткости, как правило, не приваривают к поясам балки; при этом торцы ребер жесткости должны быть плотно пригнаны к верхнему поясу балки. В балках под краны групп режимов работы 7К (в цехах металлургических производств) и 8К по ГОСТ 25546 необходимо строгать торцы, примыкающие к верхнему поясу.
В балках под краны групп режимов работы 1К - 5К по ГОСТ 25546 допускается применять односторонние поперечные ребра жесткости из полосовой стали или одиночных уголков с приваркой их к стенке и к верхнему поясу и расположением согласно 16.5.5.
16.7 ЛИСТОВЫЕ КОНСТРУКЦИИ
16.7.1 Контур поперечных элементов жесткости оболочек проектируют замкнутым.
16.7.2 Передачу сосредоточенных нагрузок на листовые конструкции, как правило, предусматривают через элементы жесткости.
16.7.3 В местах сопряжений оболочек различной формы применяют, как правило, плавные переходы в целях уменьшения местных напряжений.
16.7.4 Выполнение всех стыковых швов предусматривают двусторонней сваркой либо односторонней сваркой с подваркой корня или на подкладках.
В проекте указывают на необходимость обеспечения плотности соединений конструкций, в которых эта плотность требуется.
16.7.5 В листовых конструкциях, как правило, применяют сварные соединения встык. Соединения листов толщиной 5 мм и менее, а также монтажные соединения допускается предусматривать внахлестку.
16.8 ВИСЯЧИЕ ПОКРЫТИЯ
16.8.1 Для конструкций из нитей, как правило, применяют канаты, пряди и высокопрочную проволоку. Допускается применение проката.
16.8.2 Кровля висячего покрытия, как правило, должна быть расположена непосредственно на несущих нитях и повторять образуемую ими форму. Допускается кровлю поднять над нитями, оперев на специальную надстроечную конструкцию, или подвесить к нитям снизу. В этом случае форма кровли может отличаться от формы провисания нитей.
16.8.3 Очертания опорных контуров назначают с учетом кривых давления от усилий в прикрепленных к ним нитях при расчетных нагрузках.
16.8.4 Для сохранения стабильности формы, которая должна обеспечивать герметичность принятой конструкции кровли, висячие покрытия рассчитывают на действие временных нагрузок, в том числе ветрового отсоса. При этом проверяют изменение кривизны покрытия по двум направлениям - вдоль и поперек нитей. Необходимая стабильность достигается с помощью конструктивных мероприятий: увеличением натяжения нити за счет веса покрытия или предварительного напряжения; созданием специальной стабилизирующей конструкции; применением изгибно-жестких нитей; превращением системы нитей и кровельных плит в единую конструкцию.
16.8.5 Сечение нити рассчитывают по наибольшему усилию, возникающему при расчетной нагрузке, с учетом изменения заданной геометрии покрытия. В сетчатых системах, кроме этого, сечение нити проверяют на усилие от действия временной нагрузки, расположенной только вдоль данной нити.
16.8.6 Вертикальные и горизонтальные перемещения нитей и усилия в них определяют с учетом нелинейности работы конструкций покрытия.
16.8.7 При расчете нитей из канатов и их закреплений значения коэффициента условий работы принимают в соответствии с таблицей 44 (раздел 18); для стабилизирующих канатов, не являющихся затяжками для опорного контура, коэффициент условий работы γc = 1.
16.8.8 Опорные узлы нитей из прокатных профилей выполняют, как правило, шарнирными.
16.9 ФЛАНЦЕВЫЕ СОЕДИНЕНИЯ
16.9.1 При проектировании фланцевых соединений:
выбирают сталь для фланцев с учетом требований приложения В;
используют высокопрочные болты, обеспечивающие возможность воспринимать поперечные усилия за счет сил трения между фланцами.
Требования по натяжению болтов, его контролю и плотности контакта между фланцами даны в СНиП 3.03.01.
16.9.2 При расчете фланцевых соединений в зависимости от конструктивного решения, характера передаваемых усилий и требований эксплуатации проверяют:
несущую способность болтового соединения;
несущую способность фрикционного соединения;
прочность фланцевых листов при изгибе;
прочность сварных швов, соединяющих фланец с основным элементом.
16.10 СОЕДИНЕНИЯ С ФРЕЗЕРОВАННЫМИ ТОРЦАМИ
В соединениях элементов с фрезерованными торцами (в стыках и базах колонн и т.п.) сжимающую силу считают полностью передающейся через торцы.
Во внецентренно сжатых элементах сварные швы и болты, включая высокопрочные, рассчитывают на максимальное растягивающее усилие от действия момента и продольной силы при наиболее неблагоприятном их сочетании, а также на сдвигающее усилие от действия поперечной силы.
16.11 МОНТАЖНЫЕ КРЕПЛЕНИЯ
16.11.1 Монтажные крепления конструкций зданий и сооружений с балками крановых путей, рассчитываемыми на усталость, а также конструкций под железнодорожные составы осуществляют сварными или фрикционными.
Болты классов точности В и С в монтажных соединениях этих конструкций допускается применять:
для крепления прогонов, элементов фонарной конструкции, связей по верхним поясам ферм (при наличии связей по нижним поясам или жесткой кровли), вертикальных связей по фермам и фонарям, а также элементов фахверка;
для крепления связей по нижним поясам ферм при наличии жесткой кровли (железобетонных или армированных плит из ячеистых бетонов, стального профилированного настила и т.п.);
для крепления стропильных и подстропильных ферм к колоннам и стропильных ферм к подстропильным при условии передачи вертикального опорного давления через столик;
для крепления разрезных балок крановых путей между собой, а также для крепления их нижнего пояса к колоннам, к которым не крепятся вертикальные связи;
для крепления балок рабочих площадок, не подвергающихся воздействию динамических нагрузок;
для крепления второстепенных конструкций.
16.11.2 Для перераспределения изгибающих моментов в элементах рамных систем каркасных зданий допускается применение в узлах соединения ригелей с колоннами стальных накладок, работающих в пластической стадии.
Накладки выполняют из сталей с пределом текучести до 345 Н/мм2.
Усилия в накладках определяют при минимальном пределе текучести σy,min = Ryn и максимальном пределе текучести σy,max = Ryn + 100 Н/мм2.
Накладки, работающие в пластической стадии, должны иметь строганые или фрезерованные продольные кромки.
16.12 ОПОРНЫЕ ЧАСТИ
16.12.1 Неподвижные шарнирные опоры с центрирующими прокладками, тангенциальные, а при весьма больших реакциях - балансирные опоры применяют при необходимости строго равномерного распределения давления под опорой.
Плоские или катковые подвижные опоры применяют в случаях, когда нижележащая конструкция должна быть разгружена от горизонтальных усилий, возникающих при неподвижном опирании балки или фермы.
Коэффициент трения в плоских подвижных опорах принимают равным 0,3, в катковых - 0,03.
16.12.2 Расчет на смятие в цилиндрических шарнирах (цапфах) балансирных опор выполняют (при центральном угле касания поверхностей, равном или большем 90°) по формуле
F/(1,25rlRlpγc) ≤ 1, (178)
где F - давление (сила) на опору;
r, l - соответственно радиус и длина шарнира;
Rlp - расчетное сопротивление местному смятию при плотном касании, принимаемое согласно требованиям 7.1.
16.12.3 Расчет на диаметральное сжатие катков производят по формуле
F/(ndlRcdγc) ≤ 1, (179)
где n - число катков;
d, l - диаметр и длина катка соответственно;
Rcd - расчетное сопротивление диаметральному сжатию катков при свободном касании, принимаемое согласно требованиям 7.1.
17 ДОПОЛНИТЕЛЬНЫЕ ТРЕБОВАНИЯ ПО ПРОЕКТИРОВАНИЮ КОНСТРУКЦИЙ ОПОР ВОЗДУШНЫХ ЛИНИЙ ЭЛЕКТРОПЕРЕДАЧИ, ОТКРЫТЫХ РАСПРЕДЕЛИТЕЛЬНЫХ УСТРОЙСТВ И КОНТАКТНЫХ СЕТЕЙ ТРАНСПОРТА
17.1 Для конструкций опор воздушных линий электропередачи (ВЛ), открытых распределительных устройств (ОРУ) и контактных сетей транспорта (КС), как правило, применяют стали С235, С245, С255, С285, С345, С345К, С375 по ГОСТ 27772, сталь марки 20 и 09Г2С по ГОСТ 8731 согласно приложению В.
В зависимости от назначения конструкций и типа их соединений различают группы:
группа 1 - сварные специальные опоры больших переходов высотой свыше 60 м;
группа 2 - сварные опоры ВЛ, кроме указанных в группе 1; сварные опоры ошиновки и под выключатели ОРУ независимо от напряжения, сварные опоры под оборудование ОРУ напряжением свыше 330 кВ; конструкции и элементы КС, связанные с натяжением проводов (тяги, штанги, хомуты), а также опоры, указанные в группе 1, при отсутствии сварных соединений;
группа 3 - сварные и болтовые опоры под оборудование ОРУ напряжением до 330 кВ, кроме опор под выключатели; конструкции и элементы несущих, поддерживающих и фиксирующих устройств КС (опоры, ригели жестких поперечин, прожекторные мачты, фиксаторы), а также конструкции группы 2, кроме КС, при отсутствии сварных соединений;
группа 4 - сварные и болтовые конструкции кабельных каналов, детали путей перекатки трансформаторов, трапы, лестницы, ограждения и другие вспомогательные конструкции и элементы ОРУ, ВЛ и КС.
17.2 Болты классов точности А, В и С для опор ВЛ высотой до 60 м и конструкций ОРУ и КС принимают как для конструкций, не рассчитываемых на усталость, а для фланцевых соединений и опор ВЛ высотой более 60 м - как для конструкций, рассчитываемых на усталость, по таблице Г.3 приложения Г.
17.3 Литые детали проектируют из углеродистой стали марок 35Л и 45Л групп отливок II и III по ГОСТ 977.
17.4 При расчетах опор ВЛ, конструкций ОРУ и КС принимают дополнительные коэффициенты условий работы по таблице 42, 17.17 и приложению Е.
Таблица 42
|
№ п.п. |
Элемент конструкций |
Коэффициент условий работы |
|
1 |
Сжатый пояс из одиночного уголка стойки свободно стоящей опоры в первых двух панелях от башмака при узловых соединениях: |
|
|
на сварке |
0,95 |
|
|
на болтах |
0,90 |
|
|
2 |
Сжатый элемент плоской решетчатой траверсы из одиночного равнополочного уголка, прикрепляемого одной полкой (рисунок 20): |
|
|
пояс, прикрепляемый к стойке опоры непосредственно двумя болтами и более, поставленными вдоль пояса траверсы |
0,90 |
|
|
пояс, прикрепляемый к стойке опоры одним болтом или через фасонку |
0,75 |
|
|
раскос и распорка |
0,75 |
|
|
3 |
Оттяжка из стального каната или пучка высокопрочной проволоки: |
|
|
для промежуточной опоры в нормальном режиме работы |
0,90 |
|
|
для анкерной, анкерно-угловой и угловой опор: |
|
|
|
в нормальном режиме работы |
0,80 |
|
|
в аварийном режиме работы |
0,90 |
|
|
Примечание - Указанные в таблице значения коэффициента условий работы не распространяются на соединения элементов в узлах. |
||
Рисунок 20 - Схема траверсы с треугольной решеткой
Для опор ВЛ, ОРУ и КС значение коэффициента надежности по ответственности γn принимают равным 1,0.
Расчет на прочность растянутых элементов опор по формуле (5) с заменой в ней значения Ry на Ru/γu не допускается.
17.5 При определении приведенной гибкости по таблице 7 наибольшую гибкость всего стержня λmax вычисляют по формулам:
для четырехгранного стержня с параллельными поясами, шарнирно опертого по концам,
для трехгранного равностороннего стержня с параллельными поясами, шарнирно опертого по концам,
λmax = 2,5l/b; (181)
для свободно стоящей стойки пирамидальной формы (рисунок 13)
λmax = 2μh/bi. (182)
Обозначения, принятые в формулах (180) - (182):
l - геометрическая длина сквозного стержня;
b - расстояние между осями поясов наиболее узкой грани стержня с параллельными поясами;
h - высота свободно стоящей стойки;
μ = 1,25(bs/bi)2 - 2,75(bs/bi) + 3,5 - коэффициент для определения расчетной длины, где bs и bi - расстояния между осями поясов пирамидальной опоры в верхнем и нижнем основаниях наиболее узкой грани соответственно.
17.6 Расчет на устойчивость при сжатии с изгибом сквозного стержня с решетками постоянного по длине сечения выполняют согласно требованиям раздела 10.
Для равностороннего трехгранного сквозного стержня с решетками постоянного по длине сечения относительный эксцентриситет вычисляют по формулам:
при изгибе в плоскости, перпендикулярной одной из граней,
m = 3,46βM/(Nb); (183)
при изгибе в плоскости, параллельной одной из граней,
m = 3βM/(Nb), (184)
где b - расстояние между осями поясов в плоскости грани;
β - коэффициент, равный 1,2 при болтовых соединениях и 1,0 - при сварных соединениях.
17.7 При расчете на устойчивость при сжатии с изгибом сквозного стержня с решетками согласно требованиям 10.3.1 и 10.3.2 значение эксцентриситета е при болтовых соединениях элементов умножают на коэффициент 1,2.
17.8 При проверке устойчивости отдельных поясов стержня сквозного сечения при сжатии с изгибом продольную силу в каждом поясе определяют с учетом дополнительного усилия Nad от изгибающего момента M, вычисляемого по деформированной схеме.
Для шарнирно опертой по концам решетчатой стойки постоянного по длине прямоугольного сечения (тип 2, таблица 7) опоры с оттяжками значение момента M в середине длины стойки при изгибе ее в одной из плоскостей x-x или y-y определяют по формуле
M = Mq + (βN/δ)(fq + fn), (185)
где Mq - изгибающий момент в середине длины стойки от поперечной нагрузки, определяемый как в балках;
β - коэффициент, принимаемый согласно 17.6;
N - продольная сила в стойке;
fq - прогиб стойки в середине длины от поперечной нагрузки, определяемый как в обычных балках с использованием приведенного момента инерции сечения Ief;
fn - 0,0013l - начальный прогиб стопки и плоскости изгиба;
δ = 1 - 0,1Nl2/(EIef).
Здесь: l - длина стойки;
Ief = Al2/λef2,
где A - площадь сечения стойки;
λef - приведенная гибкость стойки, определяемая по таблице 7 для сечения типа 2 с заменой в формуле (16) λmax на λx или λy соответственно плоскости изгиба.
При изгибе стойки в двух плоскостях усилие Nad определяют по формуле (109); при этом начальный прогиб fn учитывают только в той плоскости, в которой составляющая усилия Nad от момента Mx или My имеет наибольшее значение.
17.9 Поперечную силу Q в шарнирно опертой по концам стойке с решетками постоянного по длине прямоугольного сечения (тип 2, таблица 7) опоры с оттяжками при сжатии с изгибом в одной из плоскостей x-x или y-y принимают постоянной по длине стойки и определяют по формуле
Q = Qmax + ![]() (fq + fn), (186)
(fq + fn), (186)
где Qmax - максимальная поперечная сила от поперечной нагрузки в плоскости изгиба, определяемая как в балках.
Остальные обозначения в формуле (186) принимают такими же, как в формуле (185).
17.10 Для шарнирно опертой по концам решетчатой стойки постоянного по длине треугольного сквозного сечения (тип 3, таблица 7) опоры с оттяжками при сжатии с изгибом в одной из плоскостей x-x или y-y значение момента M в середине ее длины определяют по формуле (185), в которой приведенная гибкость должна определяться по таблице 7 для сечения типа 3.
При изгибе стойки в двух плоскостях значение усилия Nad принимают большим из двух значений, определяемых по формулам:
Nad = 1,16Mx/b или Nad = 0,58Mx/b + My/b. (187)
При учете обоих моментов Mx и My во второй формуле (187) начальный прогиб стойки в каждой из двух плоскостей принимают равным fn = 0,001l.
17.11 Поперечную силу Q в плоскости грани в шарнирно опертой по концам решетчатой стойке треугольного сквозного сечения опоры с оттяжками при сжатии с изгибом определяют по формуле (186) с учетом приведенной гибкости λef, определяемой по таблице 7 для сечения типа 3.
17.12 Расчет на устойчивость сжатых элементов конструкций из одиночных уголков (поясов, решетки) выполняют, как правило, с учетом эксцентричного приложения продольной силы.
Допускается рассчитывать эти элементы как центрально-сжатые по формуле (7) при условии умножения продольных сил на коэффициенты αm и αd, принимаемые не менее 1,0.
В пространственных болтовых конструкциях по рисунку 13 (кроме рисунка 13, в и концевых опор) при центрировании в узле элементов из одиночных равнополочных уголков по их рискам при однорядном расположении болтов в элементах решетки и прикреплении раскосов в узле с двух сторон полки пояса значения коэффициентов αm и αd определяются:
для поясов при ![]() ≤ 3,5 (при
≤ 3,5 (при ![]() > 3,5 принимают
> 3,5 принимают ![]() = 3,5) по формулам:
= 3,5) по формулам:
при 0,55 ≤ c/b ≤ 0,66 и Nmd/Nm ≤ 0,7
αm = 1 + [c/b -
0,55
+ ![]() (0,2
- 0,05
(0,2
- 0,05![]() )]Nmd/Nm; (188)
)]Nmd/Nm; (188)
при 0,4 ≤ c/b < 0,55 и Nmd/Nm ≤ (2,33c/b - 0,58)
αm = 0,95 + 0,1c/b + [0,34 - 0,62c/b +
![]() (0,2
- 0,05
(0,2
- 0,05![]() )]Nmd/Nm; (189)
)]Nmd/Nm; (189)
для раскосов, примыкающих к рассчитываемой панели пояса, по формулам:
при 0,55 ≤ c/b ≤ 0,66 и Nmd/Nm < 0,7
αd = 1,18 - 0,36c/b + (1,8c/b - 0,86)Nmd/Nm; (190)
при 0,4 ≤ c/b < 0,55 и Nmd/Nm ≤ (2,33c/b - 0,58)
αd = 1 - 0,04c/b + (0,36 - 0,41c/b)Nmd/Nm. (191)
Для пространственных болтовых конструкций по рисунку 13, г, д в формулах (189) и (191) принимают 0,45 ≤ c/b < 0,55.
В формулах (190) и (191) отношение расстояния по полке уголка раскоса от обушка до риски, на которой установлены болты, к ширине полки уголка раскоса принято от 0,54 до 0,6; при отношении, равном 0,5, коэффициент αd, вычисленный по формулам (190) и (191), должен быть увеличен на 5 %.
В пространственных сварных конструкциях из одиночных равнополочных уголков по рисунку 13, б, г (кроме концевых опор) с прикреплением раскосов в узле только с внутренней стороны полки пояса при Nmd/Nm ≤ 0,7 значения коэффициентов αm и αd принимают:
при центрировании в узлах элементов по центрам тяжести сечений αm = αd = 1,0;
при центрировании в узлах осей раскосов на обушок пояса αm = αd = 1,0 + 0,12Nmd/Nm.
При расчете конструкций на совместное действие вертикальных и поперечных нагрузок и крутящего момента, вызванного обрывом проводов или тросов, допускается принимать αm = αd = 1,0.
Обозначения, принятые в формулах (188) - (191):
c - расстояние по полке уголка пояса от обушка до риски, на которой расположен центр узла;
b - ширина полки уголка пояса;
Nm - продольная сила в панели пояса;
Nmd - сумма проекций на ось пояса усилий в раскосах, примыкающих к одной полке пояса, передаваемая на него в узле и определяемая при том же сочетании нагрузок, как для Nm; при расчете пояса принимается большее из значений Nmd, полученных для узлов по концам панели, а при расчете раскосов - для узла, к которому примыкает раскос.
17.13 Расчетные длины lef и радиусы инерции сечений i при определении гибкости элементов плоских траверс с поясами и решеткой из одиночных уголков (рисунок 20) принимают равными:
для пояса lef = lm, i = imin, lef = lm1, i = ix;
для раскоса lef = ld, i = imin;
для распорки lef = lc, i = imin,
где ix - радиус инерции сечения относительно оси, параллельной плоскости решетки траверсы.
17.14 Гибкость первого снизу раскоса из одиночного уголка решетчатой свободно стоящей опоры ВЛ не должна превышать 160.
17.15 Отклонения верха опор и прогибы траверс не должны превышать значений, приведенных в таблице 43.
Таблица 43
|
№ п.п. |
Конструкция и направление отклонения |
Относительное отклонение верха опоры (к высоте опоры) |
Относительный прогиб траверсы и балки (к пролету или длине консоли) |
|||
|
Вертикальный |
Горизонтальный |
|||||
|
в пролете |
на консоли |
в пролете |
на консоли |
|||
|
1 |
Концевая и угловая опора ВЛ анкерного типа высотой до 60 м вдоль проводов |
1 120 |
1 200 |
1 70 |
Не ограничивается |
|
|
2 |
Опора ВЛ анкерного типа высотой до 60 м вдоль проводов |
1 100 |
1 200 |
1 70 |
То же |
|
|
3 |
Промежуточная опора ВЛ (кроме переходной) вдоль проводов |
Не ограничивается |
1 150 |
1 50 |
» |
|
|
4 |
Переходные опоры ВЛ всех типов высотой свыше 60 м вдоль проводов |
1 140 |
1 200 |
1 70 |
» |
|
|
5 |
Опора ОРУ вдоль проводов |
1 100 |
1 200 |
1 70 |
1 200 |
1 70 |
|
6 |
То же, поперек проводов |
1 70 |
Не ограничивается |
Не ограничивается |
Не ограничивается |
|
|
7 |
Стойка опоры под оборудование |
1 100 |
- |
- |
- |
- |
|
8 |
Балка под оборудование |
- |
1 300 |
1 250 |
|
|
|
Примечания 1 Отклонение опор ОРУ и траверс опор ВЛ в аварийном и монтажном режимах не нормируется. 2 Отклонения и прогибы по позициям 7 и 8 должны быть уменьшены, если техническими условиями на эксплуатацию оборудования установлены более жесткие требования. |
||||||
17.16 В стальных пространственных конструкциях опор ВЛ и ОРУ из одиночных уголков следует предусматривать в поперечных сечениях диафрагмы, которые должны располагаться в стойках свободно стоящих опор не реже, чем через 25 м, и в стойках опор на оттяжках - не реже, чем через 15 м. Диафрагмы должны также устанавливаться в местах приложения сосредоточенных нагрузок и переломов поясов.
17.17 При расчете на смятие соединяемых элементов решетки в одноболтовых соединениях с расстоянием от края элемента до центра отверстия вдоль усилия менее 1,5d учитывают примечание 2 таблицы 37.
В одноболтовых соединениях элементов, постоянно работающих на растяжение (тяг траверс, элементов, примыкающих к узлам крепления проводов и тросов, и в местах крепления оборудования), расстояние от края элемента до центра отверстия вдоль усилия принимают не менее 2d.
17.18 Раскосы, прикрепляемые к поясу болтами в одном узле, должны располагаться, как правило, с двух сторон полки поясного уголка.
17.19 В болтовых стыках поясных равнополочных уголков число болтов в стыке назначают четным и распределяют болты поровну между полками уголка.
Количество болтов при однорядном и шахматном их расположении, а также количество поперечных рядов болтов при двухрядном их расположении назначают, как правило, не более пяти на одной полке уголка с каждой стороны от стыка.
Указанное количество болтов и поперечных рядов допускается увеличить до семи при условии уменьшения значения коэффициента γb, определяемого по таблице 38, умножением на 0,85.
17.20 Расчет на устойчивость стенок опор из многогранных труб при числе граней от 8 до 12 выполняют по формуле
σ1/(σcrγc) ≤ 1, (192)
где σ1 - наибольшее сжимающее напряжение в сечении опоры при ее расчете по деформированной схеме;
σcr - критическое напряжение, вычисляемое по формуле
В формуле (193) обозначено:
β = 0,58 + 1,81/![]() ;
;
![]() - условная гибкость стенки грани шириной b и толщиной t.
- условная гибкость стенки грани шириной b и толщиной t.
ψ = 1 + 0,033![]() (1
- σ2/σ1),
(1
- σ2/σ1),
где ![]() принимают не более 2,4;
принимают не более 2,4;
σ2 - наименьшее напряжение в сечении, принимаемое при растяжении со знаком «минус».
Многогранные трубы должны отвечать требованиям 12.2.1 и 12.2.2 для круглых труб с радиусом описанной окружности.
18 ДОПОЛНИТЕЛЬНЫЕ ТРЕБОВАНИЯ ПО ПРОЕКТИРОВАНИЮ КОНСТРУКЦИЙ АНТЕННЫХ СООРУЖЕНИЙ СВЯЗИ ВЫСОТОЙ ДО 500 м
18.1 Для стальных конструкций антенных сооружений (АС), как правило, применяют стали по ГОСТ 27772 (кроме сталей С390К, С590, С590К), сталь марок 20 и 09Г2С по ГОСТ 8731 согласно приложению В. При этом принимают распределение конструкций по группам:
группа 1 - элементы (механические детали) оттяжек мачт и антенных полотен, детали крепления оттяжек к фундаментам и к стволам стальных опор;
группа 2 - элементы комбинированных опор;
группа 3 - стволы мачт и башен, решетка, элементы опирания на фундаменты;
группа 4 - диафрагмы башенных опор, лестницы, переходные площадки.
Материалы для соединений принимают согласно разделу 6, нормативные и расчетные сопротивления материалов и соединений - согласно разделу 7 и приложениям В и Г.
18.2 Для оттяжек и элементов антенных полотен применяют стальные канаты круглые оцинкованные по группе СС, грузовые нераскручивающиеся одинарной свивки (спиральные) или нераскручивающиеся двойной крестовой свивки с металлическим сердечником (круглопрядные), при этом спиральные канаты применяют при расчетных усилиях до 325 кН. В канатах применяют стальную круглую канатную проволоку наибольших диаметров марки 1. Для средне- и сильноагрессивных сред допускаются канаты, оцинкованные по группе ЖС, с требованиями для канатов группы СС. Допускается применение раскручивающихся канатов при условии, что обвязки из мягкой оцинкованной проволоки, расположенные по концам канатов, будут увеличены по длине на 25 %.
Для оттяжек со встроенными изоляторами орешкового типа применяют стальные канаты с неметаллическими сердечниками, если это допускается радиотехническими требованиями.
Для оттяжек с усилиями, превышающими несущую способность канатов из круглой проволоки, допускается применение стальных канатов закрытого типа из зетообразных и клиновидных оцинкованных проволок.
18.3 Концы стальных канатов в стаканах или муфтах закрепляют заливкой цинковым сплавом ЦАМ9-1,5Л по ГОСТ 21437.
18.4 Для элементов антенных полотен применяют провода согласно таблице Д.2 приложения Д. Применение медных проволок допускается только в случаях технологической необходимости.
18.5 Значение расчетного сопротивления (усилия) растяжению проводов и проволок принимают равным значению разрывного усилия, установленному государственными стандартами, деленному на коэффициент надежности по материалу γm:
для алюминиевых и медных проводов γm = 2,5;
для сталеалюминиевых проводов при номинальных сечениях, мм2:
16 и 25 - γm = 2,8; 35 - 95 - γm = 2,5; 120 и более - γm = 2,2;
для биметаллических сталемедных проволок γm = 2,0.
18.6 При расчетах конструкций АС принимают коэффициенты условий работы, установленные в разделах 5 и 15 и в таблице 44.
18.7 Относительные отклонения опор (по высоте) не должны превышать значений (кроме отклонений опор, для которых установлены иные значения техническим заданием на проектирование):
при ветровой или гололедной нагрузке................................................................ 1/100;
при односторонней подвеске антенны к опоре при отсутствии ветра............. 1/300.
18.8 Монтажные соединения элементов конструкций, передающие расчетные усилия, проектируют, как правило, на болтах класса точности В и высокопрочных болтах. При знакопеременных усилиях, как правило, принимают соединения на высокопрочных болтах или на монтажной сварке.
Применение монтажной сварки или болтов класса точности А должно быть согласовано с монтирующей организацией.
18.9 Раскосы с гибкостью более 250 при перекрестной решетке в местах пересечений должны быть скреплены между собой.
Таблица 44
|
Элементы конструкции |
Коэффициент условий работы γc |
|
Предварительно напряженные элементы решетки |
0,90 |
|
Фланцы: |
|
|
кольцевого типа |
1,10 |
|
остальных типов |
0,90 |
|
Стальные канаты оттяжек мачт или элементы антенных полотен при их количестве: |
|
|
3 - 5 оттяжек в ярусе или элементов антенных полотен |
0,80 |
|
6 - 8 оттяжек в ярусе |
0,90 |
|
9 оттяжек в ярусе и более |
0,95 |
|
Заделка концов на коуше зажимами или точечная опрессовка во втулке |
0,75 |
|
Оплетка каната на коуше или изоляторе |
0,55 |
|
Элементы крепления оттяжек, антенных полотен, проводов, подкосов к опорным конструкциям и анкерным фундаментам |
0,90 |
|
Анкерные тяжи без резьбовых соединений при работе их на растяжение с изгибом |
0,65 |
|
Проушины при работе на растяжение |
0,65 |
|
Детали креплений и соединений стальных канатов: |
|
|
механические, кроме осей шарниров |
0,80 |
|
оси шарниров при смятии |
0,90 |
Прогибы распорок диафрагм и элементов технологических площадок в вертикальной и горизонтальной плоскостях не должны превышать 1/250 пролета.
18.10 В конструкциях решетчатых опор диафрагмы должны устанавливаться на расстоянии между ними не более трех размеров среднего поперечного сечения секций опоры, а также в местах приложения сосредоточенных нагрузок и переломов поясов.
18.11 Болты фланцевых соединений труб размещают на одной окружности минимально возможного диаметра, как правило, на равных расстояниях между болтами.
18.12 Элементы решетки ферм, сходящиеся в одном узле, центрируют на ось пояса в точке пересечения их осей. В местах примыкания раскосов к фланцам допускается их расцентровка, но не более чем на треть размера поперечного сечения пояса.
В прорезных фасонках для крепления раскосов из круглой стали конец прорези рассверливают отверстием диаметром в 1,2 раза больше диаметра раскоса.
18.13 Оттяжки в мачтах с решетчатым стволом центрируют в точку пересечения осей поясов и распорок. За условную ось оттяжек принимают хорду.
Листовые проушины для крепления оттяжек подкрепляют ребрами жесткости, предохраняющими их от изгиба.
Конструкции узлов крепления оттяжек, которые не вписываются в транспортные габариты секций ствола мачт, проектируют на отдельных вставках в стволе в виде жестких габаритных диафрагм.
18.14 Натяжные устройства (муфты), служащие для регулировки длины и закрепления оттяжек мачт, должны крепиться к анкерным устройствам гибкой канатной вставкой. Длина канатной вставки между торцами втулок должна быть не менее 20 диаметров каната.
18.15 Для элементов АС применяют типовые механические детали, прошедшие испытания на прочность и усталость.
Резьбу на растянутых элементах принимают согласно ГОСТ 8724, ГОСТ 9150, ГОСТ 24705 (исполнение впадины резьбы с закруглением).
18.16 В оттяжках мачт, на проводах и канатах горизонтальных антенных полотен для гашения вибрации предусматривают последовательную установку парных низкочастотных (1 - 2,5 Гц) и высокочастотных (4 - 40 Гц) виброгасителей рессорного типа. Низкочастотные гасители выбирают в зависимости от частоты основного тона оттяжки, провода или каната. Расстояние s от концевой заделки каната до места подвески гасителей определяют по формуле
![]() (194)
(194)
где d - диаметр каната, провода, мм;
m - масса 1 м каната, провода, кг;
P - предварительное натяжение в канате, проводе, Н.
Высокочастотные гасители устанавливаются выше низкочастотных на расстоянии s. При пролетах проводов и канатов антенных полотен, превышающих 300 м, гасители устанавливают независимо от расчета.
Для гашения колебаний типа «галопирование» изменяют свободную длину каната (провода) поводками.
18.17 Антенные сооружения радиосвязи необходимо окрашивать согласно требованиям по маркировке и светоограждению высотных препятствий в соответствии с наставлением по аэродинамической службе в гражданской авиации.
19 ДОПОЛНИТЕЛЬНЫЕ ТРЕБОВАНИЯ ПО ПРОЕКТИРОВАНИЮ КОНСТРУКЦИЙ ЗДАНИЙ И СООРУЖЕНИЙ ПРИ РЕКОНСТРУКЦИИ
19.1 ОБЩИЕ ПОЛОЖЕНИЯ
19.1.1 Проектное решение принимают на основе специального обследования конструкций и вывода об их техническом состоянии, которое может быть определено как:
исправное - при выполнении всех требований действующих норм и государственных стандартов:
работоспособное - при частичном отступлении от требований норм без нарушения требований по предельным состояниям первой группы (ГОСТ 27751) и при таких нарушениях требований по предельным состояниям второй группы, которые в конкретных условиях не ограничивают нормальную эксплуатацию здания (сооружения);
ограниченно работоспособное - в случаях, когда для обеспечения эксплуатации здания (сооружения) необходим контроль за состоянием конструкций, за продолжительностью их эксплуатации или за параметрами технологических процессов (например, ограничение грузоподъемности мостовых кранов);
аварийное - при нарушении или невозможности предотвратить возможное нарушение требований по предельным состояниям первой группы.
19.1.2 При усилении или изменении условий работы сохраняемых конструкций обеспечивают как минимум их работоспособное состояние.
Конструкции, находящиеся в ограниченно работоспособном состоянии, при обеспечении необходимого контроля допускается не усиливать на период от проведения обследования до реконструкции.
19.1.3 Для конструкций, запроектированных по ранее действовавшим нормам и техническим условиям, допускается не проводить поверочный расчет в случаях, если за период эксплуатации не менее 15 лет в них не возникли дефекты и повреждения, не изменились условия дальнейшей эксплуатации, нагрузки и воздействия, а при их изменении не увеличились усилия в основных элементах.
19.1.4 При усилении конструкций предусматривают конструктивные решения и методы производства работ, обеспечивающие плавное включение элементов и конструкций усиления в совместную работу с сохраняемыми конструкциями. В необходимых случаях используют искусственное регулирование усилий и временную разгрузку конструкций.
19.2 РАСЧЕТНЫЕ ХАРАКТЕРИСТИКИ СТАЛИ И СОЕДИНЕНИЙ
19.2.1 Оценку качества материала конструкций производят по данным заводских сертификатов или по результатам испытаний образцов. Испытания выполняют при отсутствии исполнительной документации или сертификатов, недостаточности имеющихся в них сведений или обнаружении повреждений, которые могли быть вызваны низким качеством металла.
19.2.2 При исследовании и испытании металла определяют следующие показатели:
химический состав - массовую долю элементов, нормируемых государственными стандартами или техническими условиями на сталь;
предел текучести, временное сопротивление и относительное удлинение при испытаниях на растяжение по ГОСТ 1497 (рекомендуется проводить испытания с построением диаграммы работы стали);
ударную вязкость по ГОСТ 9454 для температур, соответствующих группе конструкций и расчетной температуре по таблице В.3 приложения В;
ударную вязкость после деформационного старения по ГОСТ 7268 для групп конструкций и расчетных температур по таблице В.3 приложения В;
в отдельных случаях макро- и микроструктуру стали.
Места отбора проб для определения перечисленных показателей, количество проб и необходимость усиления мест вырезки устанавливает организация, производящая обследование конструкций.
19.2.3 Исследования и испытания металла конструкций, изготовленных до 1932 г., проводят в специализированных научно-исследовательских институтах, где, кроме свойств металла, устанавливается способ производства стали: пудлинговая, конвертерная с продувкой воздухом (бессемеровская или томасовская), мартеновская или электросталь.
19.2.4 Расчетные сопротивления проката, гнутых профилей и труб сохраняемых конструкций назначают согласно требованиям 7.1, при этом значения Ryn, Run и γm принимают:
для металла конструкций, изготовленных до 1932 г., - по полученным при испытаниях минимальным значениям предела текучести и временного сопротивления; γm = 1,2; Ry для пудлинговой стали должно быть не более 170 Н/мм2, для конвертерной, мартеновской и электростали - не более 210 Н/мм2;
для металла конструкций, изготовленных после 1932 г.:
а) при наличии сертификата - по минимальным значениям предела текучести и временного сопротивления в государственных стандартах и технических условиях, по которым изготовлена данная металлопродукция; γm = 1,025 для проката, изготовленного по ГОСТ 27772; γm = 1,05 для проката, изготовленного после 1982 г. по ГОСТ 380 и ГОСТ 19281; γm = 1,1 - для всего остального проката;
б) при отсутствии сертификата (по результатам исследований металла согласно 9.6, а также сведениям о виде проката и времени строительства определяются марка стали и нормативный документ, по которому изготовлена данная металлопродукция) - по минимальным значениям предела текучести и временного сопротивления в нормативном документе для данной продукции; γm = 1,1;
в) в случаях когда идентифицировать сталь не удалось, - по минимальному результату испытаний; γm = 1,1; Ry не должно быть больше 210 Н/мм2.
Допускается не производить испытания металла конструкций, в элементах которых нормальные напряжения не выше 165 Н/мм2.
19.2.5 Расчетные сопротивления сварных соединений сохраняемых конструкций назначают с учетом марки стали, сварочных материалов, видов сварки, положения швов и способов их контроля, примененных в конструкциях.
При отсутствии установленных нормами необходимых данных допускается принимать:
для угловых швов - Rwf = Rwz = 0,44Run; βf = 0,7 и βz = 1,0, принимая при этом γc = 0,8;
для растянутых стыковых швов - Rwy = 0,55Ry в конструкциях, изготовленных до 1972 г., и Rwy = 0,85Ry - после 1972 г. Допускается уточнять несущую способность сварных соединений по результатам испытаний образцов, взятых из конструкции.
19.2.6 Расчетные сопротивления срезу и растяжению болтов, а также смятию элементов, соединяемых болтами, определяют согласно указаниям 10.2.2. Если невозможно установить класс прочности болтов, то значения расчетных сопротивлений одноболтовых соединений принимают: Rbs = 150 Н/мм2 и Rbt = 160 Н/мм2.
19.2.7 Расчетные сопротивления заклепочных соединений принимают по таблице 45.
Таблица 45
|
Условное обозначение |
Группа соединения |
Расчетное сопротивление заклепочного соединения, Н/мм2 |
|||
|
срезу и растяжению заклепок из стали марок |
смятию соединяемых элементов |
||||
|
Ст2, Ст3 |
09Г2 |
||||
|
Срез |
Rrs |
В |
180 |
220 |
- |
|
С |
160 |
- |
- |
||
|
Растяжение (отрыв головки) |
Rrt |
В, С |
120 |
150 |
- |
|
Смятие |
Rrp |
В |
- |
- |
Rrp = 2Ry |
|
С |
- |
- |
Rrp = 1,7Ry |
||
|
Примечания 1 К группе В относятся соединения, в которых заклепки поставлены в отверстия, сверленные в собранных элементах или в деталях по кондукторам. К группе С относятся соединения, в которых заклепки поставлены в отверстия, продавленные или сверленные без кондуктора в отдельных деталях. 2 При применении заклепок с потайными или полупотайными головками расчетные сопротивления заклепочных соединений срезу и смятию понижаются умножением на коэффициент 0,8. Работа указанных заклепок на растяжение не допускается. |
|||||
Если в исполнительной документации отсутствуют указания о способе образования отверстий и материале заклепок и установить их по имеющимся данным не представляется возможным, расчетные сопротивления принимают по таблице 45 как для соединений на заклепках группы С из стали марки Ст2.
Расчет заклепочных соединений выполняют согласно формулам 15.2.9, принимая Rbs = Rrs; Rbp = Rrp; Rbt = Rrt; Ab = Abn = Ar = 0,785dr2; γb = 1; db = dr.
19.3 УСИЛЕНИЕ КОНСТРУКЦИЙ
19.3.1 Конструкции, эксплуатируемые при положительной температуре и изготовленные из кипящей малоуглеродистой стали, а также из других сталей, у которых по результатам испытаний значения ударной вязкости ниже гарантированных государственными стандартами по сталям для групп конструкций в соответствии с требованиями приложения В, не подлежат усилению или замене при условии, что напряжения в элементах из этих сталей не будут превышать значений, имевшихся до реконструкции. Решение об использовании, усилении или замене этих конструкций, если эксплуатация их не будет соответствовать указанному условию, принимают на основании заключения специализированного научно-исследовательского института.
19.3.2 Расчетную схему конструкции принимают с учетом особенностей ее действительной работы, в том числе с учетом фактических отклонений геометрической формы, размеров сечений, условий закрепления и выполнения узлов сопряжения элементов.
Проверочные расчеты элементов конструкций и их соединений выполняют с учетом обнаруженных дефектов и повреждений, коррозионного износа, фактических условий сопряжения и опирания. Расчет элементов допускается выполнять по деформированной схеме, принимая при этом коэффициент условий работы γc = 1,0 для позиций 4 и 5 по таблице 1.
19.3.3 Конструкции, не удовлетворяющие требованиям разделов 8 - 10, 12 - 15 и 16.7.1 - 16.7.5, 18.2, а также требованиям СНиП 2.01.07 по ограничению вертикальных прогибов, должны быть, как правило, усилены или заменены, за исключением случаев, указанных в данном разделе.
Отклонения от геометрической формы, размеров элементов и соединений от номинальных, превышающие допускаемые ГОСТ 23118 и СНиП 3.03.01, но не препятствующие нормальной эксплуатации, могут не устраняться при условии обеспечения несущей способности конструкций с учетом требований 19.3.1.
19.3.4 Допускается не усиливать элементы конструкций, если:
их горизонтальные и вертикальные прогибы и отклонения превышают предельные значения, установленные СНиП 2.01.07 (раздел 14), но не препятствуют нормальной эксплуатации исходя из технологических требований;
их гибкость превышает предельные значения, установленные 11.3.1, но искривления элементов не превышают значений, установленных СНиП 3.03.01, и усилия в элементах не будут возрастать в процессе дальнейшей эксплуатации, а также в тех случаях, когда возможность использования таких элементов проверена расчетом или испытаниями.
19.3.5 При усилении конструкций допускается учитывать возможность предварительного напряжения и активного регулирования усилий (в том числе за счет сварки, изменений конструктивной и расчетной схем), а также упруго-пластическую работу стали, закритическую работу тонкостенных элементов и обшивок конструкций в соответствии с действующими нормами.
19.3.6 Конструкции усиления и методы его выполнения должны предусматривать меры по снижению нежелательных дополнительных деформаций элементов в процессе усиления в соответствии с 5.3.4.
Несущую способность конструкций в процессе выполнения работ по усилению обеспечивают с учетом влияния ослаблений сечений дополнительными отверстиями под болты и влияния сварки.
В необходимых случаях в период усиления конструкция должна быть полностью или частично разгружена.
19.3.7 В конструкциях 2-й, 3-й и 4-й групп (согласно приложению В), эксплуатируемых при расчетной температуре не ниже минус 45 °С в неагрессивной или слабоагрессивной среде, для обеспечения совместной работы деталей усиления и существующей конструкции допускается применять прерывистые фланговые швы.
Во всех случаях применения угловых швов, как правило, назначают минимально необходимые катеты. Допускается концевые участки швов проектировать с катетом, большим, чем катет промежуточных участков, и устанавливать их размеры в соответствии с расчетом.
19.3.8 При усилении элементов конструкций допускается применять комбинированные соединения: заклепочные с фрикционными; заклепки с болтами класса точности А.
19.3.9 В элементах групп конструкций 1, 2, 3 или 4 (согласно приложению В), подверженных при усилении нагреву вследствие сварки, расчетное напряжение σd не должно превышать значений 0,2Ry; 0,4Ry; 0,6Ry или 0,8Ry соответственно.
Напряжение σd определяют от нагрузок, действующих во время усиления, для неусиленного сечения с учетом фактического состояния конструкций (ослаблений сечения, искривлений элемента и др.).
При превышении указанных напряжений необходимы разгрузка конструкций или подведение временных опор.
19.3.10 При расчете элементов конструкций, усиленных путем увеличения сечения, как правило, учитывают разные расчетные сопротивления материалов конструкции и усиления. Допускается принимать одно расчетное сопротивление, равное меньшему из них, если они отличаются не более чем на 15 %.
19.3.11 При расчете на устойчивость элементов при центральном сжатии и сжатии с изгибом допускается принимать для усиленного сечения в целом приведенное значение расчетного сопротивления, вычисляемое по формуле
Ry,ef = Ry√k, (195)
где Ry - расчетное сопротивление основного металла, определяемое согласно требованиям 19.2.4;
k - коэффициент, вычисляемый по формуле
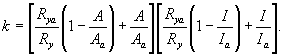 (196)
(196)
Здесь Rya - расчетное сопротивление металла усиления;
A, I - площадь и момент инерции неусиленного сечения элемента соответственно относительно оси, перпендикулярной плоскости проверки устойчивости;
Aa, Ia - то же, усиленного сечения элемента в целом.
19.3.12 Расчет на прочность и устойчивость элементов, усиленных способом увеличения сечений, как правило, выполняют с учетом напряжений, существовавших в элементе в момент усиления (с учетом разгрузки конструкций). При этом учитывают начальные искривления элементов, смещение центра тяжести усиленного сечения и искривления, вызванные сваркой.
Искривления от сварки при проверке устойчивости элементов при центральном сжатии и сжатии с изгибом допускается учитывать введением дополнительного коэффициента условий работы γc,ad = 0,8.
Проверку на прочность элементов, для которых согласно 19.3.10 допускается принимать одно расчетное сопротивление, кроме расчета по формулам (44), (45) и (90), допускается выполнять на полное расчетное усилие без учета напряжений, существовавших до усиления, а при проверке устойчивости стенок допускается использовать дополнительный коэффициент условий работы γc,ad = 0,8.
19.3.13 Расчет на прочность элементов конструкций, усиливаемых методом увеличения сечений, выполняют по формулам:
а) для центрально-растянутых симметрично усиливаемых элементов - по формуле (5);
б) для центрально-сжатых симметрично усиливаемых элементов
N/(ARyγNγc) ≤ 1, (197)
где γN = 0,95 - при усилении без использования сварки;
γN = 0,95 - 0,25σd/Ry - при усилении с использованием сварки;
в) для несимметрично усиливаемых центрально-растянутых, центрально-сжатых и внецентренно сжатых элементов
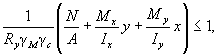 (198)
(198)
где γM = 0,95 - для конструкций группы 1;
γM = 1 - для конструкций групп 2, 3 и 4;
при N/(ARy) ≥ 0,6 принимают γM = γN, здесь γN определяют как в формуле (197).
Изгибающие моменты Mx и My определяют относительно главных осей усиленного сечения.
19.3.14 Допускается не усиливать существующие стальные конструкции, выполненные с отступлением от требований 15.1.7, 15.1.10, 15.2.2, 16.1.1 - 16.1.3, 16.2.1, 16.2.3, 16.3.3 - 16.3.5, 16.4.2, 16.4.5, 16.5.2, 16.5.4, 16.11.1, 17.14, 17.16, 18.8 - 18.11, 18.16, при условии, что:
отсутствуют вызванные этими отступлениями повреждения элементов конструкций;
исключены изменения в неблагоприятную сторону условий эксплуатации конструкций;
несущая способность и жесткость обоснованы расчетом с учетом требований 19.3.2, 19.3.4, 19.3.9;
выполняются мероприятия по предупреждению усталостного и хрупкого разрушения конструкций, на которые распространяются указания 13.1.1, 13.1.3 и раздела 14.
При выполнении этих условий для проверок устойчивости центрально-сжатых элементов допускается принимать кривую устойчивости типа b вместо типа c.
ПРИЛОЖЕНИЕ А
(справочное)
ПЕРЕЧЕНЬ НОРМАТИВНЫХ ДОКУМЕНТОВ И СТАНДАРТОВ, НА КОТОРЫЕ ИМЕЮТСЯ ССЫЛКИ В НАСТОЯЩЕМ СВОДЕ ПРАВИЛ
СНиП 2.01.07-85* Нагрузки и воздействия
СНиП 2.03.11-85 Защита строительных конструкций от коррозии
СНиП 2.09.03-85 Сооружения промышленных предприятий
СНиП 3.03.01-87 Несущие и ограждающие конструкции
СНиП 21-01-97* Пожарная безопасность зданий и сооружений
СНиП 23-01-99* Строительная климатология
ГОСТ 380-94 Сталь углеродистая обыкновенного качества. Марки
ГОСТ 535-88 Прокат сортовой и фасонный из стали углеродистой обыкновенного качества. Общие технические требования
ГОСТ 839-80 Провода неизолированные для воздушных линий электропередачи. Технические условия
ГОСТ 977-88 Отливки стальные. Общие технические условия
ГОСТ 1050-88 Прокат сортовой, калиброванный, со специальной отделкой поверхности из углеродистой качественной конструкционной стали. Общие технические условия
ГОСТ 1497-84 Металлы. Методы испытания на растяжение
ГОСТ 1759.0-87 Болты, винты, шпильки и гайки. Технические условия
ГОСТ 1759.4-87 Болты, винты и шпильки. Механические свойства и методы испытаний
ГОСТ 1759.5-87 Гайки. Механические свойства и методы испытаний
ГОСТ 2246-70 Проволока стальная сварочная. Технические условия
ГОСТ 3062-80 Канат одинарной свивки типа ЛК-О конструкции 1 ´ 7(1 + 6). Сортамент
ГОСТ 3063-80 Канат одинарной свивки типа ТК конструкции 1 ´ 19(1 + 6 + 12). Сортамент
ГОСТ 3064-80 Канат одинарной свивки типа ТК конструкции 1 ´ 37(1 + 6 + 12 + 18). Сортамент
ГОСТ 3066-80 Канат двойной свивки типа ЛК-О конструкции 6 ´ 7(1 + 6) + 1 ´ 7(1 + 6). Сортамент
ГОСТ 3067-88 Канат стальной двойной свивки типа ТК конструкции 6 ´ 19(1 + 6 + 12) + 1 ´ 19(1 + 6 + 12). Сортамент
ГОСТ 3068-88 Канат стальной двойной свивки типа ТК конструкции 6 ´ 37(1 + 6 + 12 + 18) + 1 ´ 37(1 + 6 + 12 + 18). Сортамент
ГОСТ 3081-80 Канат двойной свивки типа ЛК-О конструкции 6 ´ 19(1 + 9 + 9) + 7 ´ 7(1 + 6). Сортамент
ГОСТ 3090-73 Канаты стальные. Канат закрытый несущий с одним слоем зетообразной проволоки и сердечником типа ТК. Сортамент
ГОСТ 3822-79 Проволока биметаллическая сталемедная. Технические условия
ГОСТ 5264-80 Ручная дуговая сварка. Соединения сварные. Основные типы, конструктивные элементы и размеры
ГОСТ 5915-70 Гайки шестигранные класса точности В. Конструкция и размеры
ГОСТ 6402-70 Шайбы пружинные. Технические условия
ГОСТ 7268-82 Сталь. Метод определения склонности к механическому старению по испытанию на ударный изгиб
ГОСТ 7372-79 Проволока стальная канатная. Технические условия
ГОСТ 7669-80 Канат двойной свивки типа ЛК-РО конструкции 6 ´ 36(1 + 7 + 7/7 + 14) + 7 ´ 7(1 + 6). Сортамент
ГОСТ 7675-73 Канаты стальные. Канат закрытый несущий с одним слоем клиновидной и одним слоем зетообразной проволоки и сердечником типа ТК. Сортамент
ГОСТ 7676-73 Канаты стальные. Канат закрытый несущий с двумя слоями клиновидной и одним слоем зетообразной проволоки и сердечником типа ТК. Сортамент
ГОСТ 8050-85 Двуокись углерода газообразная и жидкая. Технические условия
ГОСТ 8713-79 Сварка под флюсом. Соединения сварные. Основные типы, конструктивные элементы и размеры
ГОСТ 8724-2002 Основные нормы взаимозаменяемости. Резьба метрическая. Диаметры и шаги
ГОСТ 8731-74 Трубы стальные бесшовные горячедеформированные. Технические условия
ГОСТ 9087-81 Флюсы сварочные плавленые. Технические условия
ГОСТ 9150-2002 Основные нормы взаимозаменяемости. Резьба метрическая. Профиль
ГОСТ 9454-78 Металлы. Метод испытания на ударный изгиб при пониженных, комнатной и повышенных температурах
ГОСТ 9467-75 Электроды покрытые металлические для ручной дуговой сварки конструкционных и теплоустойчивых сталей. Типы
ГОСТ 10157-79 Аргон газообразный и жидкий. Технические условия
ГОСТ 10605-94 Гайки шестигранные с диаметром резьбы свыше 48 мм класса точности В. Технические условия
ГОСТ 10705-80 Трубы стальные электросварные. Технические условия
ГОСТ 10706-76 Трубы стальные электросварные прямошовные. Технические требования
ГОСТ 10906-78 Шайбы косые. Технические условия
ГОСТ 11371-78 Шайбы. Технические условия
ГОСТ 11474-76 Профили стальные гнутые. Технические условия
ГОСТ 11533-75 Автоматическая и полуавтоматическая дуговая сварка под флюсом. Соединения сварные под острыми и тупыми углами. Основные типы, конструктивные элементы и размеры
ГОСТ 11534-75 Ручная дуговая сварка. Соединения сварные под острыми и тупыми углами. Основные типы, конструктивные элементы и размеры
ГОСТ 14637-89 Прокат толстолистовой из углеродистой стали обыкновенного качества. Технические условия
ГОСТ 14771-76 Дуговая сварка в защитном газе. Соединения сварные. Основные типы, конструктивные элементы и размеры
ГОСТ 14776-79 Дуговая сварка. Соединения сварные точечные. Основные типы, конструктивные элементы и размеры
ГОСТ 14954-80 Канат двойной свивки типа ЛК-Р конструкции 6 ´ 19(1 + 6 + 6/6) + 7 ´ 7(1 + 6). Сортамент
ГОСТ 16523-97 Прокат тонколистовой из углеродистой стали качественной и обыкновенного качества общего назначения. Технические условия
ГОСТ 17066-94 Прокат тонколистовой из стали повышенной прочности. Технические условия
ГОСТ 18123-82 Шайбы. Общие технические условия
ГОСТ 18126-94 Болты и гайки с диаметром резьбы свыше 48 мм. Общие технические условия
ГОСТ 18901-73 Канаты стальные. Канат закрытый несущий с двумя слоями зетообразной проволоки и сердечником типа ТК. Сортамент
ГОСТ 19281-89 Прокат из стали повышенной прочности. Общие технические условия
ГОСТ 21437-95 Сплавы цинковые антифрикционные. Марки, технические требования и методы испытаний
ГОСТ 21780-83 Система обеспечения точности геометрических параметров в строительстве. Расчет точности
ГОСТ 22353-77 Болты высокопрочные класса точности В. Конструкция и размеры
ГОСТ 22354-77 Гайки высокопрочные класса точности В. Конструкция и размеры
ГОСТ 22355-77 Шайбы класса точности С к высокопрочным болтам. Конструкция и размеры
ГОСТ 22356-77 Болты и гайки высокопрочные и шайбы. Общие технические условия
ГОСТ 23118-99 Конструкции стальные строительные. Общие технические условия
ГОСТ 23518-79 Дуговая сварка в защитных газах. Соединения сварные под острыми и тупыми углами. Основные типы, конструктивные элементы и размеры
ГОСТ 24705-81 Основные нормы взаимозаменяемости. Резьба метрическая. Основные размеры
ГОСТ 24379.0-80 Болты фундаментные. Общие технические условия
ГОСТ 24839-81 Конструкции строительные стальные. Расположение отверстий в прокатных профилях. Размеры
ГОСТ 25546-82 Краны грузоподъемные. Режимы работы
ГОСТ 26271-84 Проволока порошковая для дуговой сварки углеродистых и низколегированных сталей. Общие технические условия
ГОСТ 27751-88 Надежность строительных конструкций и оснований. Основные положения по расчету
ГОСТ 27772-88 Прокат для строительных конструкций. Общие технические условия
ГОСТ 28870-90 Сталь. Методы испытания на растяжение толстолистового проката в направлении толщины
ГОСТ 30245-2003 Профили стальные гнутые замкнутые сварные квадратные и прямоугольные для строительных конструкций. Технические условия
ТУ 14-1-5399-2000 Прокат толстолистовой с повышенной огнестойкостью для стальных строительных конструкций.
ПРИЛОЖЕНИЕ Б
(справочное)
ОСНОВНЫЕ БУКВЕННЫЕ ОБОЗНАЧЕНИЯ ВЕЛИЧИН, ИНДЕКСЫ БУКВЕННЫХ ОБОЗНАЧЕНИЙ И ПОЯСНЯЮЩИЕ ИХ СЛОВА
Б.1 ОСНОВНЫЕ БУКВЕННЫЕ ОБОЗНАЧЕНИЯ ВЕЛИЧИН
A - площадь сечения брутто;
Abn - площадь сечения болта нетто;
Ad - площадь сечения раскосов;
Af - площадь сечения полки (пояса);
An - площадь сечения нетто;
Aw - площадь сечения стенки;
Awf - площадь сечения по металлу углового шва;
Awz - площадь сечения по металлу границы сплавления;
E - модуль упругости;
F - сила;
G - модуль сдвига;
I - момент инерции сечения брутто;
Ib - момент инерции сечения ветви;
Im; Id - моменты инерции сечения пояса и раскосов фермы;
Ir - момент инерции сечения ребра, планки;
Irl - момент инерции сечения продольного ребра;
It - момент инерции при свободном кручении;
Ix; Iy - моменты инерции сечения брутто относительно осей x-x и y-y соответственно;
Ixn; Iyn - то же, сечения нетто;
Iω - секториальный момент инерции сечения;
M - момент, изгибающий момент;
Mx; My - моменты относительно осей x-x и y-y соответственно;
N - продольная сила;
Nad - дополнительное усилие;
Nbm - продольная сила от момента в ветви колонны;
Q - поперечная сила, сила сдвига;
Qfic - условная поперечная сила для соединительных элементов;
Qs - условная поперечная сила, приходящаяся на систему планок, расположенных в одной плоскости;
Rba - расчетное сопротивление растяжению фундаментных болтов;
Rbh - расчетное сопротивление растяжению высокопрочных болтов;
Rbp - расчетное сопротивление смятию одноболтового соединения;
Rbs - расчетное сопротивление срезу одноболтового соединения;
Rbt - расчетное сопротивление растяжению одноболтового соединения;
Rbun - нормативное сопротивление стали болтов, принимаемое равным временному сопротивлению σв по государственным стандартам и техническим условиям на болты;
Rbu - расчетное сопротивление растяжению U-образных болтов;
Rbyn - нормативное сопротивление стали болтов, принимаемое равным пределу текучести σт по государственным стандартам и техническим условиям на болты;
Rcd - расчетное сопротивление диаметральному сжатию катков (при свободном касании в конструкциях с ограниченной подвижностью);
Rdh - расчетное сопротивление растяжению высокопрочной проволоки;
Rlp - расчетное сопротивление местному смятию в цилиндрических шарнирах (цапфах) при плотном касании;
Rp - расчетное сопротивление стали смятию торцевой поверхности (при наличии пригонки);
Rs - расчетное сопротивление стали сдвигу;
Ru - расчетное сопротивление стали растяжению, сжатию, изгибу по временному сопротивлению;
Run - временное сопротивление стали, принимаемое равным минимальному значению σв по государственным стандартам и техническим условиям на сталь;
Rv - расчетное сопротивление стали усталости;
Rwf - расчетное сопротивление угловых швов срезу (условному) по металлу шва;
Rwu - расчетное сопротивление стыковых сварных соединений растяжению, сжатию, изгибу по временному сопротивлению;
Rwun - нормативное сопротивление металла шва по временному сопротивлению;
Rws - расчетное сопротивление стыковых сварных соединений сдвигу;
Rwy - расчетное сопротивление стыковых сварных соединений растяжению, сжатию, изгибу по пределу текучести;
Rwz - расчетное сопротивление угловых швов срезу (условному) по металлу границы сплавления;
Ry - расчетное сопротивление стали растяжению, сжатию, изгибу по пределу текучести;
Ryf - то же, для полки (пояса);
Ryw - то же, для стенки;
Ryn - предел текучести стали, принимаемый равным значению предела текучести σт по государственным стандартам и техническим условиям на сталь;
S - статический момент сдвигаемой части сечения брутто относительно нейтральной оси;
Wx; Wy - моменты сопротивления сечения брутто относительно осей x-x и y-y соответственно;
Wс; Wt - моменты сопротивления сечения для сжатой и растянутой полки соответственно;
Wxn; Wyn - моменты сопротивления сечения нетто относительно осей x-x и y-y соответственно;
b - ширина;
bef - расчетная ширина;
bf - ширина полки (пояса);
br - ширина выступающей части ребра, свеса;
cx; cy - коэффициенты для расчета с учетом развития пластических деформаций при изгибе относительно осей x-x, y-y соответственно;
d - диаметр отверстия болта;
db - наружный диаметр стержня болта;
e - эксцентриситет силы;
h - высота;
hef - расчетная высота стенки;
hw - высота стенки;
i - радиус инерции сечения;
imin - наименьший радиус инерции сечения;
ix; iy - радиусы инерции сечения относительно осей x-x и y-y соответственно;
kf - катет углового шва;
l - длина, пролет;
lc - длина стойки, колонны, распорки;
ld - длина раскоса;
lef - расчетная длина;
lm - длина панели пояса фермы или колонны;
ls - длина планки;
lw - длина сварного шва;
lx; ly - расчетные длины элемента в плоскостях, перпендикулярных осям x-x и y-y соответственно;
m - относительный эксцентриситет, m = eA/Wc;
r - радиус;
t - толщина;
tf - толщина полки (пояса);
tw - толщина стенки;
αf - отношение площадей сечений полки (пояса) и стенки αf = Af/Aw;
βf; βz - коэффициенты для расчета углового шва соответственно по металлу шва и по металлу границы сплавления;
γb - коэффициент условий работы болтового соединения;
γc - коэффициент условий работы;
γf - коэффициент надежности по нагрузке;
γm - коэффициент надежности по материалу;
γn - коэффициент надежности по ответственности;
γs - коэффициент надежности по устойчивости;
γu - коэффициент надежности в расчетах по временному сопротивлению;
η - коэффициент влияния формы сечения;
λ - гибкость, λ = lef/i;
![]() - условная гибкость,
- условная гибкость, ![]()
λef - приведенная гибкость стержня сквозного сечения;
![]() - условная приведенная гибкость стержня сквозного сечения
- условная приведенная гибкость стержня сквозного сечения ![]()
![]() - условная гибкость свеса пояса
- условная гибкость свеса пояса ![]()
![]() - условная гибкость поясного листа
- условная гибкость поясного листа ![]()
![]() - условная гибкость стенки,
- условная гибкость стенки, ![]()
![]() -
предельная условная гибкость свеса пояса
(поясного листа);
-
предельная условная гибкость свеса пояса
(поясного листа);
![]() -
предельная условная гибкость стенки;
-
предельная условная гибкость стенки;
λx; λy - расчетные гибкости элемента в плоскостях, перпендикулярных осям x-x и y-y соответственно;
v - коэффициент поперечной деформации стали (Пуассона);
σloc - местное напряжение;
σx; σy - нормальные напряжения, параллельные осям x-x и y-y соответственно;
τ - касательное напряжение;
φx(y) - коэффициент устойчивости при сжатии;
φb - коэффициент устойчивости при изгибе;
φe - коэффициент устойчивости при сжатии с изгибом;
φexy - коэффициент устойчивости при сжатии с изгибом в двух плоскостях.
Б.2 ИНДЕКСЫ БУКВЕННЫХ ОБОЗНАЧЕНИЙ И ПОЯСНЯЮЩИЕ ИХ СЛОВА
a - анкерный (anchor);
a - осевой, центральный (axial);
b - балка (beam);
b - болт (bolt);
c - сжатие (compression);
c - колонна, стойка (column);
c - пояс колонны (chord of column);
d - расчетный (design);
d - раскос (diagonal);
e - эксцентриситет (excentricity);
f - пояс, полка балки (flang);
f - сила (force);
f - трение (friction);
f - шов сварной угловой (fillet weld);
h - высокопрочный (highstrength);
i - нижний (inferior);
l - продольный (longitudinal);
m - средний (middle);
m - момент (moment);
m - материал (material);
n - нормативный (normative);
n - нетто (net);
p - смятие, давление (pressure);
r - заклепка (rivet);
r - ребро (rib);
s - сдвиг, срез (shear);
s - верхний (super);
s - устойчивость (stability);
t - растяжение (tension);
u - предельный (ultimate);
u - временное сопротивление (ultimate strength);
v - вибрация (vibration);
w - стенка балки (web);
w - сварка (welding);
y - предел текучести (yield point);
z - зона (zone);
abs - абсолютный (absolute);
ad - дополнительный (additional);
cr - критический (critical);
ef - эффективный (effective);
fic - фиктивный (fictitious);
loc - местный (local);
max - максимальный (maximum);
min - минимальный (minimum);
rel - относительный (relative).
Примечание - Двух- и трехбуквенные индексы отделяются от других индексов запятой.
ПРИЛОЖЕНИЕ В
(справочное)
МАТЕРИАЛЫ ДЛЯ СТАЛЬНЫХ КОНСТРУКЦИЙ. ГРУППЫ СТАЛЬНЫХ КОНСТРУКЦИЙ
Группа 1. Сварные конструкции1 либо их элементы, работающие в особо тяжелых условиях, в том числе максимально стесняющих развитие пластических деформаций, или подвергающиеся непосредственному воздействию динамических2, вибрационных или подвижных нагрузок (подкрановые балки; балки рабочих площадок; балки путей подвижного транспорта; элементы конструкций бункерных и разгрузочных эстакад, непосредственно воспринимающих нагрузки от подвижных составов; главные балки и ригели рам при динамической нагрузке; пролетные строения транспортерных галерей; фасонки ферм; стенки, окрайки днищ, кольца жесткости, плавающие крыши, покрытия резервуаров и газгольдеров; бункерные балки; оболочки параболических бункеров; стальные оболочки свободно стоящих дымовых труб; сварные специальные опоры больших переходов линий электропередачи (ВЛ) высотой более 60 м; элементы оттяжек мачт и оттяжечных узлов).
1 Конструкция или ее элемент считаются имеющими сварные соединения, если они расположены в местах действия значительных расчетных растягивающих напряжений (σ > 0,3Ry; σ > 0,3Rwf или σ > 0,3Rwz) либо в местах, где возможно разрушение сварного соединения, например из-за значительных остаточных напряжений, что может привести к непригодности к эксплуатации конструкции в целом.
2 Конструкции относятся к подвергающимся воздействию динамических нагрузок, если отношение абсолютного значения нормального напряжения, вызванного динамической нагрузкой, к суммарному растягивающему напряжению от всех нагрузок в том же сечении α > 0,2.
Группа 2. Сварные конструкции либо их элементы, работающие при статической нагрузке при наличии поля растягивающих напряжений (фермы; ригели рам; балки перекрытий и покрытий; косоуры лестниц; оболочки силосов; опоры ВЛ, за исключением сварных опор больших переходов; опоры ошиновки открытых распределительных устройств подстанций (ОРУ); опоры транспортерных галерей; прожекторные мачты; элементы комбинированных опор антенных сооружений (АС) и другие растянутые, растянуто-изгибаемые и изгибаемые элементы), а также конструкции и их элементы группы 1 при отсутствии сварных соединений.
Группа 3. Сварные конструкции либо их элементы, работающие при статической нагрузке преимущественно на сжатие (колонны и стойки; опорные плиты; элементы настила перекрытий; конструкции, поддерживающие технологическое оборудование; вертикальные связи по колоннам с напряжениями в связях свыше 0,4Ry; анкерные, несущие и фиксирующие конструкции (опоры, ригели жестких поперечин, фиксаторы) контактной сети транспорта; опоры под оборудование ОРУ, кроме опор под выключатели; элементы стволов и башен АС; колонны бетоновозных эстакад; прогоны покрытий и другие сжатые и сжато-изгибаемые элементы, а также конструкции и их элементы группы 2 при отсутствии сварных соединений.
Группа 4. Вспомогательные конструкции зданий и сооружений (связи, кроме указанных в группе 3; элементы фахверка; лестницы; трапы; площадки; ограждения; металлоконструкции кабельных каналов; вспомогательные элементы сооружений и т.п.), а также конструкции и их элементы группы 3 при отсутствии сварных соединений.
Примечания
1 При назначении стали в конструкциях зданий и сооружений I уровня ответственности по ГОСТ 27751 номер группы конструкций уменьшается на единицу (для групп 2 - 4).
2 При толщине проката t > 40 мм номер группы конструкций уменьшается на единицу (для групп 2 - 4), при толщине проката t ≤ 8 мм - увеличивается на единицу (для групп 1 - 3). При этом прокат толщиной 25 мм и более для элементов сварных конструкций, работающих на растяжение в направлении толщины, и остальной прокат толщиной более 40 мм должны удовлетворять требованиям ГОСТ 28870: для конструкций группы 1 - уровня ответственности I (по ГОСТ 27751), требованиям группы качества Z35; для других конструкций группы 1, а также для фланцевых соединений и в случае, когда усилие нормально поверхности листа, - требованиям группы качества Z25; в остальных случаях - Z15.
Таблица В.1 - Назначение сталей в конструкциях и сооружениях
|
Стали по |
Условия применения стали при расчетной температуре, °С |
|||||||||||
|
t ≥ -45 |
-45 > t ≥ -55 |
t < -55 |
||||||||||
|
для групп конструкций |
||||||||||||
|
ТУ 14-1-5399 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
|||
|
С235 |
Ст3кп2 |
|
|
- |
- |
+ |
- |
- |
- |
- |
- |
- |
|
С245 |
Ст3пс5 |
|
|
- |
+ |
´ |
- |
- |
- |
- |
- |
- |
|
С255, С285 |
Ст3сп5 |
|
|
+ |
´ |
´ |
- |
- |
- |
- |
- |
- |
|
С345 |
|
09Г2С |
|
3 12 |
1 4 |
1 4 |
3 12 |
3 12 |
1 4 |
4 15 |
4 15 |
2 или 3 7 или 12 |
|
|
|
|
06МБФ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
|
Обозначения, принятые в таблице В.1: знак «+» - следует применять; «-» - не следует применять; «´» - можно применять при соответствующем технико-экономическом обосновании. Примечания 1 Расчетная температура устанавливается согласно 5.1.3. 2 При использовании сталей С345 и 09Г2С в числителе даны категории требований по ударной вязкости по ГОСТ 27772, в знаменателе - аналогичные категории по ГОСТ 19281. 3 В конструкциях группы 4 при t ≥ -45 °С назначают сталь С235 по ГОСТ 27772 или Ст3кп2 и Ст3пс2 по ГОСТ 535 или ГОСТ 14637, при более низких расчетных температурах - стали С245, С255, С285 по ГОСТ 27772 или Ст3пс5 и Ст3сп5 по ГОСТ 535 или по ГОСТ 14637. 4 Прокат повышенной огнестойкости 06МБФ по ТУ 14-1-5399 имеет свойства стали С345-4 по ГОСТ 27772. 5 Прокат из стали с пределом текучести Ryn ≥ 390 Н/мм2 назначается согласно требованиям таблиц В.3 и В.4. 6 Стали для конструкций, возводимых в районах с расчетной температурой t < -45 °С, но эксплуатируемых в отапливаемых помещениях, принимают как для средней месячной температуры воздуха в январе согласно указаниям СНиП 2.01.07 (см. карту 5 приложения 5). |
||||||||||||
Таблица В.2 - Стали для труб
|
Марка стали (толщина, мм) |
ГОСТ |
Условие применения стали при расчетной температуре, °С |
||||||||
|
t ≥ -45 |
-45 > t ≥ -55 |
t < -55 |
||||||||
|
для групп конструкций |
||||||||||
|
2 |
3 |
4 |
2 |
3 |
4 |
2 |
3 |
4 |
||
|
ВСт3кп (до 4) |
+2*** |
+2*** |
+2*** |
+2*** |
+2*** |
+2*** |
- |
- |
+2*** |
|
|
ВСт3кп (4,5 - 10) |
- |
+2*** |
+2*** |
- |
- |
- |
- |
- |
- |
|
|
ВСт3пс (до 5,5) |
4-2*** |
+2*** |
+2*** |
- |
+2*** |
+2*** |
- |
- |
+2*** |
|
|
ВСт3пс (6 - 10) |
+6 |
+6 |
+6 |
- |
- |
+6 |
- |
- |
+6 |
|
|
ВСт3сп (6 - 10) |
- |
- |
- |
- |
+5 |
- |
- |
- |
- |
|
|
ВСт3пс (5 - 15) |
- |
+4 |
+4 |
- |
- |
+4 |
- |
- |
- |
|
|
ВСт3сп (5 - 15) |
- |
- |
- |
- |
+4 |
- |
- |
- |
- |
|
|
20**** |
+ |
+ |
- |
- |
- |
- |
- |
- |
- |
|
|
09Г2С**** |
+ |
+ |
- |
+ |
+ |
- |
- |
- |
- |
|
|
Обозначения, принятые в таблице В.2: «+» - следует применять; «-» - не следует применять; цифра у знака «+» означает категорию стали. * Группа В, таблица 1 ГОСТ 10705. ** Группа В с дополнительными требованиями по 5.1.4 ГОСТ 10706. *** Кроме опор ВЛ, ОРУ и КС. **** Бесшовные горячедеформированные трубы из указанных марок стали допускается применять для элементов специальных опор больших переходов ВЛ высотой более 60 м (группа конструкций 1). Примечание - Бесшовные горячедеформированные трубы из стали марки 20 по ГОСТ 8731 при расчетной температуре t ≥ -45 °С с дополнительными требованиями по ударной вязкости при температуре минус 20 °С - не менее 30 Дж/см2; из стали марки 09Г2С по ГОСТ 8731 при расчетной температуре -45 > t, °С ≥ -55 с дополнительными требованиями по ударной вязкости: при температуре минус 40 °С - не менее 40 Дж/см2 при толщине стенки до 9 мм и 35 Дж/см2 при толщине стенки 10 мм и более. |
||||||||||
Таблица В.3 - Нормируемые показатели ударной вязкости проката
|
Расчетные температуры, °С |
Группа конструкций |
Нормируемые показатели ударной вязкости для проката с пределом текучести, Н/мм2 |
|||
|
Ryn < 290 |
290 ≤ Ryn < 390 |
390 ≤ Ryn < 490 |
Ryn ≥ 490 |
||
|
t ≥ -45 |
1 |
KCA + KCV |
KCV-20 |
KCV-40 |
KCV-60 |
|
2 |
То же |
То же |
То же |
То же |
|
|
3 |
» |
» |
» |
» |
|
|
-45 > t ≥ -55 |
1 |
KCA + KCV-20 |
KCV-40 |
KCV-40 |
KCV-60 |
|
2 |
KCA + KCV0 |
KCV-20 |
То же |
То же |
|
|
3 |
То же |
То же |
» |
» |
|
|
t < -55 |
1 |
KCA + KCV-20 |
KCV-40 |
KCV-60 |
KCV-60 |
|
2 |
То же |
То же |
То же |
То же |
|
|
3 |
» |
» |
» |
» |
|
|
Примечания 1 KCV - ударная вязкость на образцах с V-образным надрезом (тип II по ГОСТ 9454), индекс t (KCVt) - регламентированная температура испытания на ударный изгиб, отсутствие индекса означает температуру +20 °С; KCA - ударная вязкость при температуре +20 °С при испытании образцов типа I по ГОСТ 9454 с V-образным надрезом после деформационного старения. 2 Нормы ударной вязкости: 1) для сталей с Ryn < 290 Н/мм2 - KCV = KCV-20 = 34 Дж/см2 на продольных образцах и 25 Дж/см2 на поперечных образцах; KCA = 29 Дж/см2; 2) для сталей с 290 ≤ Ryn < 390 Н/мм2 - KCV0 = KCV-20 = KCV-40 = 34 Дж/см2 на продольных образцах и 25 Дж/см2 на поперечных образцах; 3) для сталей с 390 ≤ Ryn < 490 Н/мм2 - KCV-40 = KCV-60 = 25 Дж/см2; 4) для сталей с Ryn ≥ 490 Н/мм2 - KCV-60 = 25 Дж/см2. |
|||||
Таблица В.4 - Требования по химическому составу
|
Нормативные сопротивления стали Ryn, Н/мм2 |
Содержание элементов1), % (не более) |
Cэ, % (не более) |
||
|
С |
Р |
S |
||
|
Ryn < 290 |
0,22 |
0,040 |
0,0502) |
- |
|
290 ≤ Ryn < 390 |
0,15 |
0,035 |
0,0402) |
0,45 |
|
390 ≤ Ryn < 490 |
0,15 |
0,0203) |
0,0153) |
0,46 |
|
490 ≤ Ryn < 590 |
0,15 |
0,015 |
0,010 |
0,47 |
|
Ryn ≥ 590 |
0,15 |
0,010 |
0,005 |
0,51 |
|
1) Предельные отклонения по химическому составу в готовом прокате по ГОСТ 27772. 2) В случае термической обработки, направленной на измельчение зерна, S ≤ 0,025 %. 3) S + P ≤ 0,020 %. Примечание - Углеродный эквивалент (Сэ, %) определяется по формуле
где C, Mn, Si, Cr, Ni, Cu, V, Nb, Mo, P - массовые доли элементов, %. |
||||
Таблица В.5 - Нормативные и расчетные сопротивления при растяжении, сжатии и изгибе листового, широкополосного универсального и фасонного проката
|
Толщина проката1), мм |
Нормативное сопротивление2) проката, Н/мм2 |
Расчетное сопротивление3) проката, Н/мм2 |
|||
|
Ryn |
Run |
Ry |
Ru |
||
|
С235 |
От 2 до 8 |
235 |
360 |
230/225 |
350/345 |
|
С245 |
От 2 до 20 |
245 |
370 |
240/235 |
360/350 |
|
Св. 20 до 30 |
235 |
370 |
230/225 |
360/350 |
|
|
С255 |
От 2 до 20 |
245 |
370 |
240/235 |
360/350 |
|
Св. 20 до 40 |
235 |
370 |
230/225 |
360/350 |
|
|
С285 |
От 2 до 10 |
275 |
390 |
270/260 |
380/370 |
|
Св. 10 до 20 |
265 |
380 |
260/250 |
370/360 |
|
|
С345 |
От 2 до 20 |
325 |
470 |
315/310 |
460/450 |
|
Св. 20 до 40 |
305 |
460 |
300/290 |
450/440 |
|
|
Св. 40 до 80 |
285 |
450 |
280/270 |
440/430 |
|
|
Св. 80 до 100 |
265 |
430 |
260/250 |
420/410 |
|
|
С345К |
От 4 до 10 |
345 |
470 |
335/330 |
460/450 |
|
С375 |
От 2 до 20 |
355 |
490 |
345/340 |
480/465 |
|
Св. 20 до 40 |
335 |
480 |
325/320 |
470/455 |
|
|
С390 |
От 4 до 50 |
390 |
540 |
380/370 |
525/515 |
|
С440 |
От 4 до 30 |
440 |
590 |
430/420 |
575/560 |
|
Св. 30 до 50 |
410 |
570 |
400/390 |
555/540 |
|
|
С590 С590К |
От 10 до 40 |
590 |
685 |
575/560 |
670/650 |
|
1) За толщину фасонного проката принимают толщину полки. 2) За нормативное сопротивление приняты гарантированные значения предела текучести и временного сопротивления, приводимые в государственных стандартах или технических условиях. В тех случаях, когда эти значения приведены только в одной системе единиц (кгс/мм2), нормативные сопротивления (Н/мм2) вычисляют умножением соответствующих величин на 9,81 с округлением до 5 Н/мм2. Допускается применение значений нормативных сопротивлений, отличных от приведенных в таблице В.5. 3) Значения расчетных сопротивлений получены делением нормативных сопротивлений на коэффициенты надежности по материалу, определенные в соответствии с таблицей 3, и округлением до 5 Н/мм2. В числителе представлены значения расчетных сопротивлений проката, поставляемого по ГОСТ 27772 (кроме стали С590К) или другой нормативной документации, в которой используется процедура контроля свойств проката по ГОСТ 27772 (γm = 1,025), в знаменателе - расчетное сопротивление остального проката при γm = 1,050. |
|||||
Таблица В.6 - Нормативные и расчетные сопротивления при растяжении, сжатии и изгибе труб
|
ГОСТ |
Толщина стенки, мм |
Нормативное сопротивление, Н/мм2 |
Расчетное сопротивление, Н/мм2 |
|||
|
Ryn |
Run |
Ry |
Ru |
|||
|
ВСт3кп, ВСт3пс, ВСт3сп |
До 10 |
225 |
370 |
215 |
350 |
|
|
ВСт3пс4, ВСт3сп4 |
4 - 15 |
245 |
370 |
235 |
350 |
|
|
20 |
4 - 36 |
245 |
410 |
225 |
375 |
|
|
Примечание - Нормативные сопротивления для труб из стали марки 09Г2С по ГОСТ 8731 устанавливаются по соглашению сторон в соответствии с требованиями этого стандарта. |
||||||
Таблица В.7 - Расчетные сопротивления проката смятию торцевой поверхности, местному смятию в цилиндрических шарнирах, диаметральному сжатию катков
|
Расчетное сопротивление, Н/мм2 |
|||
|
смятию |
диаметральному сжатию катков (при свободном касании в конструкциях с ограниченной подвижностью) Rcd |
||
|
торцевой поверхности (при наличии пригонки) Rp |
местному в цилиндрических шарнирах (цапфах) при плотном касании Rlp |
||
|
360 |
351/343 |
176/171 |
9/9 |
|
370 |
361/352 |
180/176 |
9/9 |
|
380 |
371/362 |
185/181 |
9/9 |
|
390 |
380/371 |
190/185 |
10/10 |
|
400 |
390/381 |
195/190 |
10/10 |
|
430 |
420/409 |
210/204 |
10/10 |
|
440 |
429/419 |
215/209 |
11/11 |
|
450 |
439/428 |
220/214 |
11/11 |
|
460 |
449/438 |
224/219 |
11/11 |
|
470 |
459/448 |
229/224 |
11/11 |
|
480 |
468/457 |
234/228 |
12/12 |
|
490 |
478/467 |
239/233 |
12/12 |
|
510 |
498/486 |
249/243 |
12/12 |
|
540 |
527/514 |
263/257 |
13/13 |
|
570 |
556/543 |
278/271 |
14/14 |
|
590 |
576/562 |
288/281 |
14/14 |
|
Примечание - В таблице указаны значения расчетных сопротивлений, вычисленные по формулам раздела 6 при γm = 1,025 (в числителе) и γm = 1,050 (в знаменателе). |
|||
Таблица В.8 - Расчетные сопротивления отливок из углеродистой стали
|
Условное обозначение |
Расчетные сопротивления, Н/мм2, отливок из углеродистой стали марок |
||||
|
15Л |
25Л |
35Л |
45Л |
||
|
Растяжение, сжатие и изгиб |
Ru |
150 |
180 |
210 |
250 |
|
Сдвиг |
Rs |
90 |
110 |
130 |
150 |
|
Смятие торцевой поверхности (при наличии пригонки) |
Rp |
230 |
270 |
320 |
370 |
|
Смятие местное в цилиндрических шарнирах (цапфах) при плоском касании |
Rlp |
110 |
130 |
160 |
180 |
|
Диаметральное сжатие катков при свободном касании (в конструкциях с ограниченной подвижностью) |
Rcd |
6 |
7 |
8 |
10 |
ПРИЛОЖЕНИЕ Г
(справочное)
МАТЕРИАЛЫ ДЛЯ СОЕДИНЕНИЙ СТАЛЬНЫХ КОНСТРУКЦИЙ
Таблица Г.1 - Материалы для сварки, соответствующие стали
|
Материалы для сварки |
|||||
|
в углекислом газе (по ГОСТ 8050) или в его смеси с аргоном (по ГОСТ 10157) |
под флюсом (по ГОСТ 9087) |
порошковой проволокой (по ГОСТ 26271) |
покрытыми электродами (по ГОСТ 9467) |
||
|
Марка |
Тип электрода |
||||
|
сварочной проволоки |
флюса |
порошковой проволоки |
|||
|
Ryn < 290 Н/мм2 |
Св-08Г2С |
Св-08А |
АН-348-А АН-60* |
ПП-АН-3 ПП-АН-8 |
Э42*, Э42А |
|
Св-08ГА |
Э46*, Э46А |
||||
|
290 Н/мм2 ≤ Ryn < 590 Н/мм2 |
Св-10ГА** |
АН-17-М АН-43 АН-47 АН-348-А*** |
Э50*, Э50А |
||
|
Св-10Г2** Св-10НМА |
- |
||||
|
Ryn ≥ 590 Н/мм2 |
Св-08Г2С Св-08ХГСМА |
Св-10НМА |
АН-17-М |
ПП-АН-3 |
Э60 |
|
Св-10ХГ2СМА |
Св-08ХН2ГМЮ |
ПП-АН-8 |
Э70 |
||
|
* Флюс АН-60 и электроды типов Э42, Э46, Э50 применяют для конструкций групп 2, 3 при расчетных температурах t ≥ -45 °С. ** Не применять в сочетании с флюсом АН-43. *** Для флюса АН-348-А требуется дополнительный контроль механических свойств металла шва при сварке соединений элементов всех толщин при расчетных температурах t < -45 °С и толщин свыше 32 мм - при расчетных температурах t ≥ -45 °С. Примечание - При соответствующем технико-экономическом обосновании для сварки конструкций допускается использовать сварочные материалы (проволоку, флюсы, защитные газы), не указанные в настоящей таблице. При этом механические свойства металла шва, выполняемого с их применением, должны быть не ниже свойств, обеспечиваемых применением материалов согласно настоящей таблице. |
|||||
Таблица Г.2 - Нормативные и расчетные сопротивления металла угловых швов
|
Rwun, Н/мм2 |
Rwf, Н/мм2 |
||
|
Тип электрода (по ГОСТ 9467) |
Марка проволоки |
||
|
Э42, Э42А |
Св-08, Св-08А |
410 |
180 |
|
Э46, Э46А |
Св-08ГА, |
450 |
200 |
|
Э50, Э50А |
Св-08Г2С, Св-10ГА, ПП-АН-8, ПП-АН-3 |
490 |
215 |
|
Э60 |
Св-08Г2С1, Св-10НМА, Св-10Г2 |
590 |
240 |
|
Э70 |
Св-10ХГ2СМА, Св-08ХН2ГМЮ |
685 |
280 |
|
Э85 |
- |
835 |
340 |
|
1 Только для швов с катетом kf ≤ 8 мм в конструкциях из стали с пределом текучести 440 Н/мм2 и более. |
|||
Таблица Г.3 - Требования к болтам при различных условиях их применения
|
Расчетная температура t, °С |
Класс прочности болтов и требования к ним по ГОСТ 1759.4 в конструкциях |
|||
|
не рассчитываемых на усталость |
рассчитываемых на усталость |
|||
|
при работе болтов на |
||||
|
растяжение или срез |
срез |
растяжение или срез |
срез |
|
|
≥ -45 |
5,6 |
5,6 |
5,6 |
5,6 |
|
8,8 |
8,8 |
8,8 |
8,8 |
|
|
10,9 |
10,9 |
10,9 |
10,9 |
|
|
- |
12,9 |
- |
12,9 |
|
|
-45 > t ≥ -55 |
5,6 |
5,6 |
5,6 |
5,6 |
|
8,8 |
8,8 |
8,8* |
8,8 |
|
|
10,9 |
10,9 |
10,9* |
10,9 |
|
|
- |
12,9 |
- |
12,9 |
|
|
< -55 |
5,6 |
5,6 |
- |
5,6 |
|
8,8* |
8,8 |
8,8* |
8,8 |
|
|
10,9* |
10,9 |
10,9* |
10,9 |
|
|
- |
12,9 |
- |
12,9 |
|
|
* С требованием испытания на разрыв на косой шайбе по 6.5 ГОСТ 1759.4. Примечание - Высокопрочные болты по ГОСТ 22356 из стали марки 40Х «селект» применяются в тех же конструкциях, что и болты класса прочности 10,9. |
||||
Таблица Г.4 - Марки стали фундаментных болтов и условия их применения
|
Нормативный документ |
Марка стали при расчетной температуре, t, °С |
|||
|
≥ -45 |
-45 > t ≥ -55 |
< -55 |
||
|
Конструкции, кроме опор воздушных линий электропередачи, распределительных устройств и контактной сети |
Ст3пс2, |
Ст3пс4, |
- |
|
|
|
Ст3сп2 |
Ст3сп4 |
- |
|
|
20 |
- |
- |
||
|
- |
09Г2С-4* |
09Г2С-4* |
||
|
Для U-образных болтов, а также фундаментных болтов опор воздушных линий электропередачи, распределительных устройств и контактной сети |
Ст3пс4, |
- |
- |
|
|
|
Ст3сп4 |
- |
- |
|
|
- |
09Г2С-4* |
09Г2С-6** |
||
|
* Допускается применение других сталей по ГОСТ 19281 категории 4. ** Допускается применение других сталей по ГОСТ 19281 категории 6. |
||||
Таблица Г.5 - Нормативные сопротивления стали болтов и расчетные сопротивления одноболтовых соединений срезу и растяжению, Н/мм2
|
Rbun |
Rbyn |
Rbs |
Rbt |
|
|
5,6 |
500 |
300 |
210 |
225 |
|
8,8 |
800 |
640 |
320 |
435 |
|
10,9 |
1000 |
900 |
400 |
540 |
|
12,9 |
1200 |
1080 |
420 |
- |
|
40Х «селект» |
1100 |
990 |
405 |
550 |
|
Примечание - Значения расчетных сопротивлений, указанные в таблице, вычислены по формулам раздела 3 с округлением до 5 Н/мм2. |
||||
Таблица Г.6 - Нормативные сопротивления стали и расчетные сопротивления смятию элементов в болтовых соединениях, Н/мм2
|
Временное сопротивление стали соединяемых элементов Run |
Rbp для болтов |
|
|
класса точности А |
классов точности В и С |
|
|
360 |
560 |
475 |
|
370 |
580 |
485 |
|
380 |
590 |
500 |
|
390 |
610 |
515 |
|
430 |
670 |
565 |
|
440 |
685 |
580 |
|
450 |
700 |
595 |
|
460 |
720 |
605 |
|
470 |
735 |
620 |
|
480 |
750 |
630 |
|
490 |
765 |
645 |
|
510 |
795 |
670 |
|
540 |
845 |
710 |
|
570 |
890 |
750 |
|
590 |
920 |
775 |
|
Примечание - Значения расчетных сопротивлений, указанные в таблице, вычислены по формулам раздела 6 с округлением до 5 Н/мм2. |
||
Таблица Г.7 - Расчетные сопротивления растяжению фундаментных болтов
|
Rba, Н/мм2, для болтов из стали марок |
||
|
по ГОСТ 5351) |
по ГОСТ 192811) |
|
|
Ст3пс4, Ст3пс2, Ст3сп4, Ст3сп2 |
09Г2С-6, 09Г2С-8 |
|
|
12, 16, 20 |
200 |
265 |
|
24, 30 |
190 |
245 |
|
36 |
190 |
230 |
|
42, 48, 56 |
180 |
230 |
|
64, 72, 80 |
180 |
220 |
|
90, 100 |
180 |
210 |
|
110, 125, 140 |
165 |
210 |
|
1) Расчетные сопротивления для болтов из других сталей вычисляются по формулам раздела 7. Примечания 1 Сталь по ГОСТ 535 должна поставляться по 1-й группе. 2 В таблице указаны значения расчетных сопротивлений, вычисленные по формулам раздела 7 с округлением до 5 Н/мм2. |
||
Таблица Г.8 - Нормативные и расчетные сопротивления, Н/мм2, растяжению высокопрочных болтов по ГОСТ 22356 из стали марки 40Х «селект»
|
Номинальный диаметр резьбы, мм |
Rbun |
Rbh |
|
16, 20, (22), 24, (27) |
1100 |
770 |
|
30 |
950 |
665 |
|
36 |
750 |
525 |
|
42 |
650 |
455 |
|
48 |
600 |
420 |
|
Примечание - Размеры, заключенные в скобки, применять не рекомендуется. |
||
Таблица Г.9 - Площади сечения болтов, см2, по ГОСТ 1759.4
|
d, мм |
16 |
(18) |
20 |
(22) |
24 |
(27) |
30 |
36 |
42 |
48 |
|
Ab |
2,01 |
2,54 |
3,14 |
3,80 |
4,52 |
5,72 |
7,06 |
10,17 |
13,85 |
18,09 |
|
Abn |
1,57 |
1,92 |
2,45 |
3,03 |
3,53 |
4,59 |
5,61 |
8,16 |
11,20 |
14,72 |
|
Примечания 1 Площади сечения болтов диаметром свыше 48 мм принимают по ГОСТ 24379.0. 2 Размеры, заключенные в скобки, не рекомендуется применять в конструкциях, кроме опор ВЛ и ОРУ. |
||||||||||
ПРИЛОЖЕНИЕ Д
(справочное)
ФИЗИЧЕСКИЕ ХАРАКТЕРИСТИКИ МАТЕРИАЛОВ
Таблица Д.1 - Физические характеристики материалов для стальных конструкций
|
Характеристики |
Значение |
|
Плотность ρ, кг/м3: |
|
|
проката и стальных отливок |
7850 |
|
отливок из чугуна |
7200 |
|
Коэффициент линейного расширения α, °С-1 |
0,12 · 10-4 |
|
Модуль упругости E, Н/мм2: |
|
|
прокатной стали, стальных отливок |
2,06 · 105 |
|
пучков и прядей параллельных проволок |
1,96 · 105 |
|
канатов стальных: |
|
|
спиральных и закрытых |
1,67 · 105 |
|
несущих: |
|
|
двойной свивки |
1,47 · 105 |
|
двойной свивки с неметаллическим сердечником |
1,27 · 105 |
|
Модуль сдвига прокатной стали и стальных отливок G, Н/мм2 |
0,79 · 105 |
|
Коэффициент поперечной деформации (Пуассона) v |
0,3 |
|
Примечание - Значения модуля упругости даны для канатов, предварительно вытянутых усилием, равным не менее 60 % разрывного усилия для канатов в целом. |
|
Таблица Д.2 - Физические характеристики проводов и проволоки
|
Марка и номинальное сечение, мм2 |
Модуль упругости E, Н/мм2 |
Коэффициент линейного расширения α, °С-1 |
|
|
Алюминиевые провода по ГОСТ 839 |
А, АНП; 16-800 |
0,630 · 105 |
0,23 · 10-4 |
|
Медные провода по ГОСТ 839 |
М; 4-800 |
1,300 · 105 |
0,17 · 10-4 |
|
Сталеалюминиевые провода по ГОСТ 839 при отношении площадей алюминия к стали, равном: |
АС, АСК; АСКП, АСКС |
|
|
|
6 - 6,25 |
10 и более |
0,825 · 105 |
0,192 · 10-4 |
|
0,65 |
95 |
1,460 · 105 |
0,139 · 10-4 |
|
4,29 - 4,39 |
120 и более |
0,890 · 105 |
0,183 · 10-4 |
|
7,71 - 8,04 |
150 и более |
0,770 · 105 |
0,198 · 10-4 |
|
1,46 |
185 и более |
1,140 · 105 |
0,155 · 10-4 |
|
12,22 |
330 |
0,665 · 105 |
0,212 · 10-4 |
|
18,2 - 18,5 |
400 и 500 |
0,665 · 105 |
0,212 · 10-4 |
|
Биметаллическая сталемедная проволока по ГОСТ 3822 диаметром, мм: |
БСМ 1 |
|
|
|
1,6 - 4 |
2,0 - 12,5 |
1,870 · 105 |
0,127 · 10-4 |
|
6 |
28,2 |
1,900 · 105 |
0,124 · 10-4 |
|
Примечание - Значения массы проводов и проволоки принимают по ГОСТ 839 и ГОСТ 3822. |
|||
ПРИЛОЖЕНИЕ Е
(рекомендуемое)
КОЭФФИЦИЕНТЫ УСЛОВИЙ РАБОТЫ ДЛЯ РАСТЯНУТОГО ОДИНОЧНОГО УГОЛКА, ПРИКРЕПЛЯЕМОГО ОДНОЙ ПОЛКОЙ БОЛТАМИ
Значения коэффициента условий работы γc1 при расчете по формуле (6) сечений растянутого одиночного уголка из стали с пределом текучести до 380 Н/мм2, прикрепляемого одной полкой болтами, поставленными в один ряд по оси, расположенной на расстояниях не менее 0,5b от обушка уголка и не менее 1,2d от пера уголка, следует определять по формуле
γc1 = (α1An1/An + α2)β, (Е.1)
где An1 - площадь части сечения прикрепляемой полки уголка между краем отверстия и пером;
An - площадь сечения уголка нетто;
α1, α2, β - коэффициенты, определяемые по таблице Е.1.
При расчете тяг и поясов траверс, элементов опор ВЛ, ОРУ и КС, непосредственно примыкающих к узлам крепления проводов, а также элементов, соединяющих в стойках узлы крепления тяг и растянутых поясов траверс, коэффициент γc1 следует уменьшить на 10 %.
Обозначения, принятые в приложении Е:
a - расстояние вдоль усилия от края элемента до центра ближайшего отверстия;
b - ширина полки уголка;
s - расстояние вдоль усилия между центрами отверстий;
d - диаметр отверстия для болта с учетом положительного допуска.
Таблица Е.1 - Коэффициенты α1, α2, β
|
Значения коэффициентов α1, α2, β |
||||||
|
при одном болте и расстоянии a, равном |
при a ≥ 1,5d и s ≥ 2d при количестве болтов в ряду |
|||||
|
1,35d1) |
1,5d |
2d |
2 |
3 |
4 |
|
|
α1 |
1,70 |
1,70 |
1,70 |
1,77 |
1,45 |
1,17 |
|
α2 |
0,05 |
0,05 |
0,05 |
0,19 |
0,36 |
0,47 |
|
β |
0,65 |
0,85 |
1,0 |
1,0 |
1,0 |
1,0 |
|
1) Только для элементов решеток (раскосов и распорок), кроме постоянно работающих на растяжение, при толщине полки до 6 мм. |
||||||
ПРИЛОЖЕНИЕ Ж
(рекомендуемое)
КОЭФФИЦИЕНТЫ ДЛЯ РАСЧЕТА НА УСТОЙЧИВОСТЬ ЦЕНТРАЛЬНО- И ВНЕЦЕНТРЕННО СЖАТЫХ ЭЛЕМЕНТОВ
Таблица Ж.1 - Коэффициент устойчивости при центральном сжатии
|
Условная гибкость |
Коэффициент φ для типов кривых устойчивости |
Условная гибкость |
Коэффициент φ для типов кривых устойчивости |
||||
|
a |
b |
c |
a |
b |
c |
||
|
0,4 |
999 |
998 |
992 |
5,4 |
261 |
261 |
255 |
|
0,6 |
994 |
986 |
950 |
5,6 |
242 |
242 |
240 |
|
0,8 |
981 |
967 |
929 |
5,8 |
226 |
226 |
226 |
|
1,0 |
968 |
948 |
901 |
6,0 |
211 |
||
|
1,2 |
954 |
927 |
878 |
6,2 |
198 |
||
|
1,4 |
938 |
905 |
842 |
6,4 |
186 |
||
|
1,6 |
920 |
881 |
811 |
6,6 |
174 |
||
|
1,8 |
900 |
855 |
778 |
6,8 |
164 |
||
|
2,0 |
877 |
826 |
744 |
7,0 |
155 |
||
|
2,2 |
851 |
794 |
709 |
7,2 |
147 |
||
|
2,4 |
820 |
760 |
672 |
7,4 |
139 |
||
|
2,6 |
785 |
722 |
635 |
7,6 |
132 |
||
|
2,8 |
747 |
683 |
598 |
7,8 |
125 |
||
|
3,0 |
704 |
643 |
562 |
8,0 |
119 |
||
|
3,2 |
660 |
602 |
526 |
8,5 |
105 |
||
|
3,4 |
615 |
562 |
492 |
9,0 |
094 |
||
|
3,6 |
572 |
524 |
460 |
9,5 |
084 |
||
|
3,8 |
530 |
487 |
430 |
10,0 |
076 |
||
|
4,0 |
475 |
453 |
401 |
10,5 |
069 |
||
|
4,2 |
431 |
421 |
375 |
11,0 |
063 |
||
|
4,4 |
393 |
392 |
351 |
11,5 |
057 |
||
|
4,6 |
359 |
359 |
328 |
12,0 |
053 |
||
|
4,8 |
330 |
330 |
308 |
12,5 |
049 |
||
|
5,0 |
304 |
304 |
289 |
13,0 |
045 |
||
|
5,2 |
281 |
281 |
271 |
14,0 |
039 |
||
|
Примечание - Значения коэффициента φ в таблице увеличены в 1000 раз. |
|||||||
Таблица Ж.2 - Коэффициент влияния формы сечения η
|
Схема сечения и эксцентриситет |
Af/Aw |
Значения η при |
||||
|
0 ≤ |
|
|||||
|
0,1 ≤ m ≤ 5 |
5 < m ≤ 20 |
0,1 ≤ m ≤ 5 |
5 ≤ m ≤ 20 |
|||
|
1 |
|
- |
1,0 |
1,0 |
1,0 |
|
|
2 |
t/h = 0,25 |
- |
0,85 |
0,85 |
0,85 |
|
|
3 |
|
- |
0,75
+ 0,02 |
0,75
+ 0,02 |
0,85 |
|
|
4 |
t/h = 0,25 |
- |
(1,35 - 0,05m) - 0,01(5 - m) |
1,1 |
1,1 |
|
|
5 |
|
0,25 |
(1,45
- 0,05m) -
0,01(5 - m) |
1,2 |
1,2 |
|
|
0,5 |
(1,75 - 0,1m) - 0,02(5 - m) |
1,25 |
1,25 |
|||
|
≥ 1,0 |
(1,90 - 0,1m) - 0,02(6 - m) |
1,4 - 0,02 |
1,3 |
|||
|
6 |
a1/h ≤ 0,15 |
- |
η5[1 - 0,3(5 - m)a1/h] |
η5 |
η5 |
|
|
7 |
a1/h < 0,15 |
- |
η5(1 - 0,8a1/h) |
η5(1 - 0,8a1/h) |
η5(1 - 0,8a1/h) |
|
|
8 |
|
0,25 |
(0,75 + 0,05m) + 0,01(5 - m) |
1,0 |
1,0 |
|
|
0,5 |
(0,5 + 0,1m) + 0,02(5 - m) |
1,0 |
1,0 |
|||
|
≥ 1 |
(0,25 + 0,15m) + 0,03(5 - m) |
1,0 |
1,0 |
|||
|
9 |
|
0,5 |
(1,25 - 0,05m) - 0,01(5 - m) |
1,0 |
1,0 |
|
|
≥ 1 |
(1,5 - 0,1m) - 0,02(5 - m) |
1,0 |
1,0 |
|||
|
10 |
|
0,5 |
1,4 |
1,4 |
1,4 |
1,4 |
|
1,0 |
1,6 - 0,01(5 - m) |
1,6 |
1,35 + 0,05m |
1,6 |
||
|
2,0 |
1,8 - 0,02(5 - m) |
1,8 |
1,3 + 0,1m |
1,8 |
||
|
11 |
|
0,5 |
1,45 + 0,04m |
1,65 |
1,45 + 0,04m |
1,65 |
|
1,0 |
1,8 + 0,12m |
2,4 |
1,8 + 0,12m |
2,4 |
||
|
1,5 |
2,0 + 0,25m + 0,1 |
- |
- |
- |
||
|
2,0 |
3,0 + 0,25m + 0,1 |
- |
- |
- |
||
|
Примечания 1 Для типов сечений 5 - 7 при подсчете значении Af/Aw площадь вертикальных элементов полок не следует учитывать. 2 Для типов сечений 6 - 7 значения η5 принимают равными значениям η для типа 5 при тех же значениях Af/Aw. |
||||||
Таблица Ж.3 - Коэффициент устойчивости φe при внецентренном сжатии сплошностенчатых стержней в плоскости действия момента, совпадающей с плоскостью симметрии
|
Условная
гибкость |
Значение φe при приведенном относительном эксцентриситете mef |
||||||||
|
0,1 |
0,25 |
0,5 |
0,75 |
1,0 |
1,25 |
1,5 |
1,75 |
2,0 |
|
|
0,5 |
967 |
922 |
850 |
782 |
722 |
669 |
620 |
577 |
538 |
|
1,0 |
925 |
854 |
778 |
711 |
653 |
600 |
563 |
520 |
484 |
|
1,5 |
875 |
804 |
716 |
647 |
593 |
548 |
507 |
470 |
439 |
|
2,0 |
813 |
742 |
653 |
587 |
536 |
496 |
457 |
425 |
397 |
|
2,5 |
742 |
672 |
587 |
526 |
480 |
442 |
410 |
383 |
357 |
|
3,0 |
667 |
597 |
520 |
465 |
425 |
395 |
365 |
342 |
320 |
|
3,5 |
587 |
522 |
455 |
408 |
375 |
350 |
325 |
303 |
287 |
|
4,0 |
505 |
447 |
394 |
356 |
330 |
309 |
289 |
270 |
256 |
|
4,5 |
418 |
382 |
342 |
310 |
288 |
272 |
257 |
242 |
229 |
|
5,0 |
354 |
326 |
295 |
273 |
253 |
239 |
225 |
215 |
205 |
|
5,5 |
302 |
280 |
256 |
240 |
224 |
212 |
200 |
192 |
184 |
|
6,0 |
258 |
244 |
223 |
210 |
198 |
190 |
178 |
172 |
166 |
|
6,5 |
223 |
213 |
196 |
185 |
176 |
170 |
160 |
155 |
149 |
|
7,0 |
194 |
186 |
173 |
163 |
157 |
152 |
145 |
141 |
136 |
|
8,0 |
152 |
146 |
138 |
133 |
128 |
121 |
117 |
115 |
113 |
|
9,0 |
122 |
117 |
112 |
107 |
103 |
100 |
098 |
096 |
093 |
|
10,0 |
100 |
097 |
093 |
091 |
090 |
085 |
081 |
080 |
079 |
|
11,0 |
083 |
079 |
077 |
076 |
075 |
073 |
071 |
069 |
068 |
|
12,0 |
069 |
067 |
064 |
063 |
062 |
060 |
059 |
059 |
058 |
|
13,0 |
062 |
061 |
054 |
053 |
052 |
051 |
051 |
050 |
049 |
|
14,0 |
052 |
049 |
049 |
048 |
048 |
047 |
047 |
046 |
045 |
Продолжение таблицы Ж.3
|
Условная гибкость |
Значение φe при приведенном относительном эксцентриситете mef |
||||||||
|
2,5 |
3,0 |
3,5 |
4,0 |
4,5 |
5,0 |
5,5 |
6,0 |
6,5 |
|
|
0,5 |
469 |
417 |
370 |
337 |
307 |
280 |
260 |
237 |
222 |
|
1,0 |
427 |
382 |
341 |
307 |
283 |
259 |
240 |
225 |
209 |
|
1,5 |
388 |
347 |
312 |
283 |
262 |
240 |
223 |
207 |
195 |
|
2,0 |
352 |
315 |
286 |
260 |
240 |
222 |
206 |
193 |
182 |
|
2,5 |
317 |
287 |
262 |
238 |
220 |
204 |
190 |
178 |
168 |
|
3,0 |
287 |
260 |
238 |
217 |
202 |
187 |
175 |
166 |
156 |
|
3,5 |
258 |
233 |
216 |
198 |
183 |
172 |
162 |
153 |
145 |
|
4,0 |
232 |
212 |
197 |
181 |
168 |
158 |
149 |
140 |
135 |
|
4,5 |
208 |
192 |
178 |
165 |
155 |
146 |
137 |
130 |
125 |
|
5,0 |
188 |
175 |
162 |
150 |
143 |
135 |
126 |
120 |
117 |
|
5,5 |
170 |
158 |
148 |
138 |
132 |
124 |
117 |
112 |
108 |
|
6,0 |
153 |
145 |
137 |
128 |
120 |
115 |
109 |
104 |
100 |
|
6,5 |
140 |
132 |
125 |
117 |
112 |
106 |
101 |
097 |
094 |
|
7,0 |
127 |
121 |
115 |
108 |
102 |
098 |
094 |
091 |
087 |
|
8,0 |
106 |
100 |
095 |
091 |
087 |
083 |
081 |
078 |
076 |
|
9,0 |
088 |
085 |
082 |
079 |
075 |
072 |
069 |
066 |
065 |
|
10,0 |
075 |
072 |
070 |
069 |
065 |
062 |
060 |
059 |
058 |
|
11,0 |
063 |
062 |
061 |
060 |
057 |
055 |
053 |
052 |
051 |
|
12,0 |
055 |
054 |
053 |
052 |
051 |
050 |
049 |
048 |
047 |
|
13,0 |
049 |
048 |
048 |
047 |
045 |
044 |
043 |
042 |
041 |
|
14,0 |
044 |
043 |
043 |
042 |
041 |
040 |
040 |
039 |
039 |
Окончание таблицы Ж.3
|
Условная гибкость |
Значение φe при приведенном относительном эксцентриситете mef |
|||||||
|
7,0 |
8,0 |
9,0 |
10 |
12 |
14 |
17 |
20 |
|
|
0,5 |
210 |
183 |
164 |
150 |
125 |
106 |
090 |
077 |
|
1,0 |
196 |
175 |
157 |
142 |
121 |
103 |
086 |
074 |
|
1,5 |
182 |
163 |
148 |
134 |
114 |
099 |
082 |
070 |
|
2,0 |
170 |
153 |
138 |
125 |
107 |
094 |
079 |
067 |
|
2,5 |
158 |
144 |
130 |
118 |
101 |
090 |
076 |
065 |
|
3,0 |
147 |
135 |
123 |
112 |
097 |
086 |
073 |
063 |
|
3,5 |
137 |
125 |
115 |
106 |
092 |
082 |
069 |
060 |
|
4,0 |
127 |
118 |
108 |
098 |
088 |
078 |
066 |
057 |
|
4,5 |
118 |
110 |
101 |
093 |
083 |
075 |
064 |
055 |
|
5,0 |
111 |
103 |
095 |
088 |
079 |
072 |
062 |
053 |
|
5,5 |
104 |
095 |
089 |
084 |
075 |
069 |
060 |
051 |
|
6,0 |
096 |
089 |
084 |
079 |
072 |
066 |
057 |
049 |
|
6,5 |
089 |
083 |
080 |
074 |
068 |
062 |
054 |
047 |
|
7,0 |
083 |
078 |
074 |
070 |
064 |
059 |
052 |
045 |
|
8,0 |
074 |
068 |
065 |
062 |
057 |
053 |
047 |
041 |
|
9,0 |
064 |
061 |
058 |
055 |
051 |
048 |
043 |
038 |
|
10,0 |
057 |
055 |
052 |
049 |
046 |
043 |
039 |
035 |
|
11,0 |
050 |
048 |
046 |
044 |
040 |
038 |
035 |
032 |
|
12,0 |
046 |
044 |
042 |
040 |
037 |
035 |
032 |
029 |
|
13,0 |
041 |
039 |
038 |
037 |
035 |
033 |
030 |
027 |
|
14,0 |
038 |
037 |
036 |
036 |
034 |
032 |
029 |
026 |
|
Примечания 1 Значения коэффициента φe в таблице увеличены в 1000 раз. 2 Значения коэффициента φe принимать не выше значений φ. |
||||||||
Таблица Ж.4 - Коэффициент устойчивости φe при внецентренном сжатии сквозных стержней в плоскости действия момента, совпадающей с плоскостью симметрии
|
Условная приведенная
гибкость |
Значение φe при относительном эксцентриситете m |
||||||||
|
0,1 |
0,25 |
0,5 |
0,75 |
1,0 |
1,25 |
1,5 |
1,75 |
2,0 |
|
|
0,5 |
908 |
800 |
666 |
571 |
500 |
444 |
400 |
364 |
333 |
|
1,0 |
872 |
762 |
640 |
553 |
483 |
431 |
387 |
351 |
328 |
|
1,5 |
830 |
727 |
600 |
517 |
454 |
407 |
367 |
336 |
311 |
|
2,0 |
774 |
673 |
556 |
479 |
423 |
381 |
346 |
318 |
293 |
|
2,5 |
708 |
608 |
507 |
439 |
391 |
354 |
322 |
297 |
274 |
|
3,0 |
637 |
545 |
455 |
399 |
356 |
324 |
296 |
275 |
255 |
|
3,5 |
562 |
480 |
402 |
355 |
320 |
294 |
270 |
251 |
235 |
|
4,0 |
484 |
422 |
357 |
317 |
288 |
264 |
246 |
228 |
215 |
|
4,5 |
415 |
365 |
315 |
281 |
258 |
237 |
223 |
207 |
196 |
|
5,0 |
350 |
315 |
277 |
250 |
230 |
212 |
201 |
186 |
178 |
|
5,5 |
300 |
273 |
245 |
223 |
203 |
192 |
182 |
172 |
163 |
|
6,0 |
255 |
237 |
216 |
198 |
183 |
174 |
165 |
156 |
149 |
|
6,5 |
221 |
208 |
190 |
178 |
165 |
157 |
149 |
142 |
137 |
|
7,0 |
192 |
184 |
168 |
160 |
150 |
141 |
135 |
130 |
125 |
|
8,0 |
148 |
142 |
136 |
130 |
123 |
118 |
113 |
108 |
105 |
|
9,0 |
117 |
114 |
110 |
107 |
102 |
098 |
094 |
090 |
087 |
|
10,0 |
097 |
094 |
091 |
090 |
087 |
084 |
080 |
076 |
073 |
|
11,0 |
082 |
078 |
077 |
076 |
073 |
071 |
068 |
066 |
064 |
|
12,0 |
068 |
066 |
064 |
063 |
061 |
060 |
058 |
057 |
056 |
|
13,0 |
060 |
059 |
054 |
053 |
052 |
051 |
050 |
049 |
049 |
|
14,0 |
050 |
049 |
048 |
047 |
046 |
046 |
045 |
044 |
043 |
Продолжение таблицы Ж.4
|
Условная приведенная гибкость |
Значение φe при относительном эксцентриситете m |
||||||||
|
2,5 |
3,0 |
3,5 |
4,0 |
4,5 |
5,0 |
5,5 |
6,0 |
6,5 |
|
|
0,5 |
286 |
250 |
222 |
200 |
182 |
167 |
154 |
143 |
133 |
|
1,0 |
280 |
243 |
218 |
197 |
180 |
165 |
151 |
142 |
131 |
|
1,5 |
271 |
240 |
211 |
190 |
178 |
163 |
149 |
137 |
128 |
|
2,0 |
255 |
228 |
202 |
183 |
170 |
156 |
143 |
132 |
125 |
|
2,5 |
238 |
215 |
192 |
175 |
162 |
148 |
136 |
127 |
120 |
|
3,0 |
222 |
201 |
182 |
165 |
153 |
138 |
130 |
121 |
116 |
|
3,5 |
206 |
187 |
170 |
155 |
143 |
130 |
123 |
115 |
110 |
|
4,0 |
191 |
173 |
160 |
145 |
133 |
124 |
118 |
110 |
105 |
|
4,5 |
176 |
160 |
149 |
136 |
124 |
116 |
110 |
105 |
400 |
|
5,0 |
161 |
149 |
138 |
127 |
117 |
108 |
104 |
100 |
095 |
|
5,5 |
147 |
137 |
128 |
118 |
110 |
102 |
098 |
095 |
091 |
|
6,0 |
135 |
126 |
119 |
109 |
103 |
097 |
093 |
090 |
085 |
|
6,5 |
124 |
117 |
109 |
102 |
097 |
092 |
088 |
085 |
080 |
|
7,0 |
114 |
108 |
101 |
095 |
091 |
087 |
083 |
079 |
076 |
|
8,0 |
097 |
091 |
085 |
082 |
079 |
077 |
073 |
070 |
067 |
|
9,0 |
082 |
079 |
075 |
072 |
069 |
067 |
064 |
062 |
059 |
|
10,0 |
070 |
067 |
064 |
062 |
060 |
058 |
056 |
054 |
052 |
|
11,0 |
060 |
058 |
056 |
054 |
053 |
052 |
050 |
048 |
046 |
|
12,0 |
054 |
053 |
050 |
049 |
048 |
047 |
045 |
043 |
042 |
|
13,0 |
048 |
047 |
046 |
045 |
044 |
044 |
042 |
041 |
040 |
|
14,0 |
043 |
042 |
042 |
041 |
041 |
040 |
039 |
039 |
038 |
Окончание таблицы Ж.4
|
Условная приведенная гибкость |
Значение φe при относительном эксцентриситете m |
|||||||
|
7,0 |
8,0 |
9,0 |
10 |
12 |
14 |
17 |
20 |
|
|
0,5 |
125 |
111 |
100 |
091 |
077 |
067 |
058 |
048 |
|
1,0 |
121 |
109 |
098 |
090 |
077 |
066 |
055 |
046 |
|
1,5 |
119 |
108 |
096 |
088 |
077 |
065 |
053 |
045 |
|
2,0 |
117 |
106 |
095 |
086 |
076 |
064 |
052 |
045 |
|
2,5 |
113 |
103 |
093 |
083 |
074 |
062 |
051 |
044 |
|
3,0 |
110 |
100 |
091 |
081 |
071 |
061 |
051 |
043 |
|
3,5 |
106 |
096 |
088 |
078 |
069 |
059 |
050 |
042 |
|
4,0 |
100 |
093 |
084 |
076 |
067 |
057 |
049 |
041 |
|
4,5 |
096 |
089 |
079 |
073 |
065 |
055 |
048 |
040 |
|
5,0 |
092 |
086 |
076 |
071 |
062 |
054 |
047 |
039 |
|
5,5 |
087 |
081 |
074 |
068 |
059 |
052 |
046 |
039 |
|
6,0 |
083 |
077 |
070 |
065 |
056 |
051 |
045 |
038 |
|
6,5 |
077 |
072 |
066 |
061 |
054 |
050 |
044 |
037 |
|
7,0 |
074 |
068 |
063 |
058 |
051 |
047 |
043 |
036 |
|
8,0 |
065 |
060 |
055 |
052 |
048 |
044 |
041 |
035 |
|
9,0 |
056 |
053 |
050 |
048 |
045 |
042 |
039 |
035 |
|
10,0 |
050 |
047 |
045 |
043 |
041 |
038 |
036 |
033 |
|
11,0 |
044 |
043 |
042 |
041 |
038 |
035 |
032 |
030 |
|
12,0 |
040 |
039 |
038 |
037 |
034 |
032 |
030 |
028 |
|
13,0 |
038 |
037 |
036 |
035 |
032 |
030 |
028 |
026 |
|
14,0 |
037 |
036 |
035 |
034 |
031 |
029 |
027 |
025 |
|
Примечания 1 Значения коэффициента φe в таблице увеличены в 1000 раз. 2 Значения коэффициента φe принимать не выше значений φ. |
||||||||
Таблица Ж.5 - Приведенные относительные эксцентриситеты mef для внецентренно сжатых стержней с шарнирно-опертыми концами
|
Очертание эпюры моментов |
|
Значение mef при mef,1, равном |
|
||||||||||
|
0,1 |
0,5 |
1,0 |
1,5 |
2,0 |
3,0 |
4,0 |
5,0 |
7,0 |
10,0 |
20,0 |
|
||
|
δ = -1,0
|
1 |
0,10 |
0,30 |
0,68 |
1,12 |
1,60 |
2,62 |
3,55 |
4,55 |
6,50 |
9,40 |
19,40 |
|
|
2 |
0,10 |
0,17 |
0,39 |
0,68 |
1,03 |
1,80 |
2,75 |
3,72 |
5,65 |
8,60 |
18,50 |
|
|
|
3 |
0,10 |
0,10 |
0,22 |
0,36 |
0,55 |
1,17 |
1,95 |
2,77 |
4,60 |
7,40 |
17,20 |
|
|
|
4 |
0,10 |
0,10 |
0,10 |
0,18 |
0,30 |
0,57 |
1,03 |
1,78 |
3,35 |
5,90 |
15,40 |
|
|
|
5 |
0,10 |
0,10 |
0,10 |
0,10 |
0,15 |
0,23 |
0,48 |
0,95 |
2,18 |
4,40 |
13,40 |
|
|
|
6 |
0,10 |
0,10 |
0,10 |
0,10 |
0,10 |
0,15 |
0,18 |
0,40 |
1,25 |
3,00 |
11,40 |
|
|
|
7 |
0,10 |
0,10 |
0,10 |
0,10 |
0,10 |
0,10 |
0,10 |
0,10 |
0,50 |
1,70 |
9,50 |
|
|
|
δ = -0,5
|
1 |
0,10 |
0,31 |
0,68 |
1,12 |
1,60 |
2,62 |
3,55 |
4,55 |
6,50 |
9,40 |
19,40 |
|
|
2 |
0,10 |
0,22 |
0,46 |
0,73 |
1,05 |
1,88 |
2,75 |
3,72 |
5,65 |
8,60 |
18,50 |
|
|
|
3 |
0,10 |
0,17 |
0,38 |
0,58 |
0,80 |
1,33 |
2,00 |
2,77 |
4,60 |
7,40 |
17,20 |
|
|
|
4 |
0,10 |
0,14 |
0,32 |
0,49 |
0,66 |
1,05 |
1,52 |
2,22 |
3,50 |
5,90 |
15,40 |
|
|
|
5 |
0,10 |
0,10 |
0,26 |
0,41 |
0,57 |
0,95 |
1,38 |
1,80 |
2,95 |
4,70 |
13,40 |
|
|
|
6 |
0,10 |
0,16 |
0,28 |
0,40 |
0,52 |
0,95 |
1,25 |
1,60 |
2,50 |
4,00 |
11,50 |
|
|
|
7 |
0,10 |
0,22 |
0,32 |
0,42 |
0,55 |
0,95 |
1,10 |
1,35 |
2,20 |
3,50 |
10,80 |
|
|
|
δ = 0
|
1 |
0,10 |
0,32 |
0,70 |
1,12 |
1,60 |
2,62 |
3,55 |
4,55 |
6,50 |
9,40 |
19,40 |
|
|
2 |
0,10 |
0,28 |
0,60 |
0,90 |
1,28 |
1,96 |
2,75 |
3,72 |
5,65 |
8,40 |
18,50 |
|
|
|
3 |
0,10 |
0,27 |
0,55 |
0,84 |
1,15 |
1,75 |
2,43 |
3,17 |
4,80 |
7,40 |
17,20 |
|
|
|
4 |
0,10 |
0,26 |
0,52 |
0,78 |
1,10 |
1,60 |
2,20 |
2,83 |
4,00 |
6,30 |
15,40 |
|
|
|
5 |
0,10 |
0,25 |
0,52 |
0,78 |
1,10 |
1,55 |
2,10 |
2,78 |
3,85 |
5,90 |
14,50 |
|
|
|
6 |
0,10 |
0,28 |
0,52 |
0,78 |
1,10 |
1,55 |
2,00 |
2,70 |
3,80 |
5,60 |
13,80 |
|
|
|
7 |
0,10 |
0,32 |
0,52 |
0,78 |
1,10 |
1,55 |
1,90 |
2,60 |
3,75 |
5,50 |
13,00 |
|
|
|
δ = 0,5
|
1 |
0,10 |
0,40 |
0,80 |
1,23 |
1,68 |
2,62 |
3,55 |
4,55 |
6,50 |
9,40 |
19,40 |
|
|
2 |
0,10 |
0,40 |
0,78 |
1,20 |
1,60 |
2,30 |
3,15 |
4,10 |
5,85 |
8,60 |
18,50 |
|
|
|
3 |
0,10 |
0,40 |
0,77 |
1,17 |
1,55 |
2,30 |
3,10 |
3,90 |
5,55 |
8,13 |
18,00 |
|
|
|
4 |
0,10 |
0,40 |
0,75 |
1,13 |
1,55 |
2,30 |
3,05 |
3,80 |
5,30 |
7,60 |
17,50 |
|
|
|
5 |
0,10 |
0,40 |
0,75 |
1,10 |
1,55 |
2,30 |
3,00 |
3,80 |
5,30 |
7,60 |
17,00 |
|
|
|
6 |
0,10 |
0,40 |
0,75 |
1,10 |
1,50 |
2,30 |
3,00 |
3,80 |
5,30 |
7,60 |
16,50 |
|
|
|
7 |
0,10 |
0,40 |
0,75 |
1,10 |
1,40 |
2,30 |
3,00 |
3,80 |
5,30 |
7,60 |
16,00 |
|
|
|
Обозначения, принятые в таблице Ж.5:
|
|||||||||||||
ПРИЛОЖЕНИЕ И
(рекомендуемое)
КОЭФФИЦИЕНТ cmax ДЛЯ РАСЧЕТА НА УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ ТОНКОСТЕННОГО ОТКРЫТОГО СЕЧЕНИЯ
И.1 Коэффициент cmax при типах сечений, приведенных в таблице И.1, вычисляют по формуле
где
α = ax/h - отношение расстояния ax между центром тяжести и центром изгиба сечения к высоте сечения h;
ex = Mx/N - эксцентриситет приложения сжимающей силы относительно оси x-x, принимаемый со своим знаком (в таблице И.1 показан со знаком «плюс»).
В формулах (И.2) обозначено:
ρ = (Ix + Iy)/(Ah2) + α2;
β - коэффициент, принимаемый по таблице И.1;
ω = Iω/(Iyh2) - здесь Iω - секториальный момент инерции сечения;
It = εΣbiti3 - момент инерции сечения при свободном кручении (здесь ε - коэффициент, принимаемый по таблице И.1; bi и ti - ширина и толщина листов, образующих сечение, включая стенку, соответственно).
Формулы для определения ω, ε, α и β и их значения приведены в таблице И.1.
При расчете стержня П-образного сечения на центральное сжатие в формуле (И.1) принимают B = 1 и ex = 0.
И.2 Коэффициент cmax при расчете на устойчивость стержня швеллерного сечения вычисляют по формуле (В.1) при значениях ε = 0,37 и β = 0; при этом принимают (Ix > Iy, рисунок И.1):
где 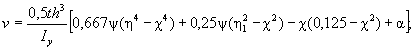
η = b/h; ψ = tf/tw, χ = η2ψ/(1 + 2ηψ);
γ = 3η2ψ/(1 + 6ηψ); η1 = η - ω.
Величины μ, ρ, ω, It определяют по формулам (И.1), (И.2), принимая Iω и α согласно формулам (И.3).
Рисунок И.1 - Схема швеллерного сечения
И.3 Расчет на устойчивость внецентренно сжатых элементов двутаврового сечения с двумя осями симметрии, непрерывно подкрепленных вдоль одной из полок (рисунок И.2), выполняют по формулам (6) и (7), в которых коэффициент cmax определяют по формуле
Рисунок И.2 - Схема сечения элемента, подкрепленного вдоль полки
Коэффициент α определяют по формуле (М.4) приложения М.
При определении α значение lef принимают равным расстоянию между сечениями элемента, закрепленными от поворота относительно продольной оси (расстояние между узлами крепления связей, распорок и т.п.).
Эксцентриситет ех = Mx/N в формуле (И.4) считается положительным, если точка приложения силы смещена в сторону свободной полки; для центрально-сжатых элементов ex = 0.
При определении ex за расчетный момент Mx принимают наибольший момент в пределах расчетной длины lef элемента.
Таблица И.1 - Коэффициенты ω, ε, α, β
|
ω |
ε |
α |
β |
|
|
|
0,25 |
0,43 |
0 |
0 |
|
|
|
0,42 |
|
|
|
|
0 |
0,40 |
h1/h |
То же |
|
|
3 + 2η (6 + η)2 |
0,37 |
4(3 + η) (2 + η)(6 + η) |
0 |
|
Обозначения, принятые в таблице И.1: I1 и I2 - моменты инерции соответственно большего и меньшего поясов относительно оси симметрии сечения y-y; η = b/h. |
||||
ПРИЛОЖЕНИЕ К
(рекомендуемое)
КОЭФФИЦИЕНТЫ ДЛЯ РАСЧЕТА НА ПРОЧНОСТЬ ЭЛЕМЕНТОВ СТАЛЬНЫХ КОНСТРУКЦИЙ
Таблица К.1 - Коэффициенты для расчета элементов с учетом развития пластических деформаций
|
Схема сечений |
Af/Aw |
Наибольшие значения коэффициентов |
|||
|
cx |
cy |
n при My = 01) |
|||
|
1 |
|
0,25 |
1,19 |
1,47 |
1,5 |
|
0,5 |
1,12 |
||||
|
1,0 |
1,07 |
||||
|
2,0 |
1,04 |
||||
|
2 |
|
0,5 |
1,40 |
1,47 |
2,0 |
|
1,0 |
1,28 |
||||
|
2,0 |
1,18 |
||||
|
3 |
|
0,25 |
1,19 |
1,07 |
1,5 |
|
0,5 |
1,12 |
1,12 |
|||
|
1,0 |
1,07 |
1,19 |
|||
|
2,0 |
1,04 |
1,26 |
|||
|
4 |
|
0,5 |
1,40 |
1,12 |
2,0 |
|
1,0 |
1,28 |
1,20 |
|||
|
2,0 |
1,18 |
1,31 |
|||
|
5 |
|
- |
1,47 |
1,47 |
а) 2,0 б) 3,0 |
|
6 |
|
0,25 |
1,47 |
1,04 |
3,0 |
|
0,5 |
1,07 |
||||
|
1,0 |
1,12 |
||||
|
2,0 |
1,19 |
||||
|
7 |
|
- |
1,26 |
1,26 |
1,5 |
|
8 |
|
- |
1,60 |
1,47 |
а) 3,0 б) 1,0 |
|
9 |
|
0,5 |
1,60 |
1,07 |
а) 3,0 б) 1,0 |
|
1,0 |
1,12 |
||||
|
2,0 |
1,19 |
||||
|
1) При My ≠ 0 принимают n = 1,5, за исключением сечения типа 5, а, для которого n = 2, и типа 5, б, для которого n = 3. Примечания 1 При определении коэффициента для промежуточных значений Af/Aw допускается линейная интерполяция. 2 Значение коэффициентов сх, су принимают не более 1,15γf, где γf - коэффициент надежности по нагрузке, определяемый как отношение расчетного значения эквивалентной (по значению изгибающего момента) нагрузки к нормативному. |
|||||
ПРИЛОЖЕНИЕ Л
(рекомендуемое)
МЕТОДИКА ПОДБОРА МИНИМАЛЬНЫХ СЕЧЕНИЙ ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ
Л.1 ОБЩИЕ ПОЛОЖЕНИЯ
Л.1.1 Методика позволяет установить размеры минимальных по площади сечений шарнирно опертых балок, нагруженных в плоскости стенки и имеющих сварное двутавровое сечение с двумя осями симметрии с устойчивой, гибкой или перфорированной стенкой, а также определить наиболее эффективное сопротивление стали.
Л.1.2 Устойчивость балок обеспечивают выполнением требований 9.4.4 - 9.4.6.
Л.1.3 Для подбора минимального сечения балки расчетными размерами и параметрами являются:
l - пролет балки;
M - расчетный изгибающий момент в балке;
n - параметр, определяющий предельный прогиб (fu = l/п) и принимаемый согласно СНиП 2.01.07 (раздел 10);
ρ - параметр, равный 9,6 - при равномерно распределенной нагрузке, 12 - при сосредоточенной нагрузке в середине пролета, 10 - в остальных случаях;
γf - коэффициент надежности по нагрузке, определяемый как отношение расчетного значения эквивалентной (по значению изгибающего момента) нагрузки к нормативному;
B
- ![]() ψ = l/B;
θ = n/(ργf) - величины,
используемые в расчетных формулах.
ψ = l/B;
θ = n/(ργf) - величины,
используемые в расчетных формулах.
Л.1.4 Для принятого с учетом действующих сортаментов минимального сечения балки, а также с учетом требований и ограничений, предъявляемых к проекту в каждом конкретном случае, выполняют проверку балки согласно требованиям раздела 9 (для балок с устойчивой стенкой) или настоящего приложения (для балок с гибкой стенкой).
Л.2 БАЛКИ ИЗ ОДНОРОДНОГО МАТЕРИАЛА С УСТОЙЧИВОЙ СТЕНКОЙ
Л.2.1 Размеры сечений двутавровых балок 1-го класса определяют по формулам:
tw = 0,367B; hw = 5,5twv/√γc;
tf = 1,66tw; bf = 0,302hw, (Л.1)
где ![]()
Эффективное значение расчетного сопротивления стали Ry,ef определяют по формуле
Л.2.2 Размеры сечений двутавровых балок 2-го
класса при ограниченных пластических деформациях ![]() (1 <
(1 < ![]() ≤ 5) определяют по формулам:
≤ 5) определяют по формулам:
![]()
![]()
где ω1 = 1 + 1/3![]() + 0,8(τ/Rs)4(1 - 1/
+ 0,8(τ/Rs)4(1 - 1/![]() );
);
α1 = 0,25(3ω1 - 2).
Параметр ![]() определяют по
формулам:
определяют по
формулам:
для балок из однородной стали
где c1x - коэффициент, определяемый по формулам (70) и изменяющийся в пределах 1 < c1x ≤ cx;
для бистальных балок
![]() = 1 + (1,3 - 0,2αf)(c1r
- 1), (Л.5)
= 1 + (1,3 - 0,2αf)(c1r
- 1), (Л.5)
где c1r - коэффициент, определяемый по формулам:
c1r = Mx/(WxnRywγc) или c1r = βrcxr (Л.6)
и изменяющийся в пределах 1 < c1r ≤ cxr;
здесь βr и cxr - коэффициенты, определяемые согласно 9.2.8.
Для балок коробчатого сечения коэффициенты c1x и c1r в формулах (Л.4) и (Л.5) соответственно умножают на 0,5.
В формулах (Л.3) значение ![]() определяют в зависимости от
определяют в зависимости от ![]() по таблице Л.1, а значение
по таблице Л.1, а значение ![]() - по формуле (80). В таблице Л.1
и формулах (Л.3) среднее
касательное напряжение τ принимают равным τ = Q/Aw, а параметр
- по формуле (80). В таблице Л.1
и формулах (Л.3) среднее
касательное напряжение τ принимают равным τ = Q/Aw, а параметр ![]() - по формулам (Л.4) - (Л.6).
- по формулам (Л.4) - (Л.6).
Таблица Л.1
|
τ/Rs |
Предельные
значения |
||||||||
|
1,0 |
1,5 |
2,0 |
2,5 |
3,0 |
3,5 |
4,0 |
4,5 |
≥ 5,0 |
|
|
0 |
5,50 |
4,00 |
3,42 |
3,00 |
2,72 |
2,52 |
2,37 |
2,27 |
2,20 |
|
0,5 |
4,50 |
3,70 |
3,13 |
2,75 |
2,51 |
2,35 |
2,26 |
2,20 |
2,20 |
|
0,6 |
4,25 |
3,52 |
2,98 |
2,64 |
2,42 |
2,28 |
2,20 |
2,20 |
2,20 |
|
0,7 |
4,00 |
3,34 |
2,84 |
2,53 |
2,34 |
2,20 |
2,20 |
2,20 |
2,20 |
|
0,8 |
3,75 |
3,04 |
2,62 |
2,37 |
2,26 |
2,20 |
2,20 |
2,20 |
2,20 |
|
0,9 |
3,50 |
2,73 |
2,39 |
2,20 |
2,20 |
2,20 |
2,20 |
2,20 |
2,20 |
Значения M и Q определяют в одном сечении балки.
Эффективное значение расчетного сопротивления стали Ry,ef определяют по формуле
где η = (1,8ω1 -
0,8)/(ω1![]() ).
).
Л.2.3 При наличии зоны чистого изгиба размеры сечений балок 2-го класса и эффективное значение расчетного сопротивления
стали определяют по формулам (Л.3)
и (Л.7) соответственно при
подстановке в них значения ![]() = 1,42.
= 1,42.
Л.2.4 Размеры сечений двутавровых балок 3-го
класса (при ![]() = 2,2;
= 2,2; ![]() = 0,3) определяют по
формулам:
= 0,3) определяют по
формулам:
![]()
![]()
![]()
![]() (Л.8)
(Л.8)
где ω2 = 1 + 0,8(τ/Rs)4;
α2 = 0,25(3ω2 - 2).
Эффективное значение расчетного сопротивления стали Ry,ef определяют по формуле
где η2 = (1,8ω2 - 0,8)/(ω2![]() ).
).
Л.2.5 При выборе стали расчетное сопротивление Ry принимают близким к Ry,ef, вычисленному по формулам (Л.2), (Л.7) и (Л.9); при этом выполняют условие Ry ≤ Ry,ef.
Л.2.6 Для балок 2-го и 3-го классов при одновременном действии в сечении M и Q в формулах (Л.3), (Л.7) - (Л.9) в первом приближении принимают τ = 0, в последующих приближениях τ = Q/(twhw).
Л.3 БИСТАЛЬНЫЕ БАЛКИ С УСТОЙЧИВОЙ СТЕНКОЙ
Л.3.1 Размеры сечений бистальных двутавровых балок 2-го класса с устойчивой стенкой при Ryf/Ryw = r определяют по формулам:
![]()
![]()
где ω3 = 2r - 1 + 1/(3r2) + 0,8(τ/Rsw)4(1 - 1/r2);
α3 = 0,25(3ω3/r - 2);
![]()
В формулах (Л.10) значение ![]() определяют по таблице
Л.1 в зависимости от параметра
определяют по таблице
Л.1 в зависимости от параметра ![]() , определяемого по формуле (Л.5).
, определяемого по формуле (Л.5).
Эффективное значение расчетного сопротивления стали стенки Ryw,ef определяют по формуле
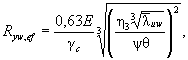 (Л.11)
(Л.11)
где η3 = (1,8ω3/r - 0,8)/(ω3![]() ).
).
При выборе стали выполняют условие Ryw ≤ Ryw,ef.
При одновременном действии в сечении M и Q учитывают положения Л.2.6.
Л.4 БАЛКИ С ГИБКОЙ СТЕНКОЙ
Л.4.1 Разрезные балки с гибкой стенкой симметричного двутаврового сечения, несущие статическую нагрузку и изгибаемые в плоскости стенки, как правило, применяют при нагрузке, эквивалентной равномерно распределенной до 50 кН/м, и проектируют из стали с пределом текучести до 345 Н/мм2.
Л.4.2 Устойчивость балок с гибкой стенкой обеспечивают либо выполнением
требований 5.18,а, либо закреплением сжатого
пояса, при котором условная гибкость пояса ![]() не превышает 0,21 (где bf - ширина сжатого
пояса).
не превышает 0,21 (где bf - ширина сжатого
пояса).
Л.4.3 Отношение ширины свеса
сжатого пояса к его толщине принимают не более ![]() .
.
Л.4.4 Отношение площадей сечений пояса и стенки αf = Af/(th) не должно превышать предельных значений αfи, определяемых по формуле
![]() (Л.12)
(Л.12)
Л.4.5 Участок стенки балки над опорой укрепляют двусторонним опорным ребром жесткости и рассчитывают его согласно требованиям 9.5.13.
На расстоянии не менее ширины ребра и не более ![]() от опорного ребра
устанавливают дополнительное двустороннее ребро жесткости размером согласно Л.4.9.
от опорного ребра
устанавливают дополнительное двустороннее ребро жесткости размером согласно Л.4.9.
Л.4.6 Местное напряжение σloc в стенке балки, определяемое по формуле (37), должно быть не более 0,75Ry, при этом значение lef вычисляют по формуле (39).
Л.4.7 При определении прогиба балок момент инерции поперечного сечения
брутто балки уменьшают умножением на коэффициент α = 1,2 - 0,033![]() для балок с ребрами в пролете и на
коэффициент α = 1,2 - 0,033
для балок с ребрами в пролете и на
коэффициент α = 1,2 - 0,033![]() - h/l
- для балок без ребер в пролете.
- h/l
- для балок без ребер в пролете.
Л.4.8 Прочность разрезных балок
симметричного двутаврового сечения, несущих статическую нагрузку, изгибаемых в
плоскости стенки, укрепленной только поперечными ребрами жесткости (рисунок Л.1), с условной гибкостью стенки 6 ≤ ![]() ≤ 13 проверяют по формуле
≤ 13 проверяют по формуле
(M/Mu)4 + (Q/Qu)4 ≤ 1, (Л.13)
где M и Q - значения момента и поперечной силы в рассматриваемом сечении балки;
Mu - предельное значение момента, вычисляемое по формуле
Mu = Ryγcth2[Af/(th)
+ (0,85/![]() )(1 - 1/
)(1 - 1/![]() )]; (Л.14)
)]; (Л.14)
Qu - предельное значение поперечной силы, вычисляемое по формуле
Qu = Rsγcth[τcr/Rs + 3,3βμ(1 - τcr/Rs)/(1 + μ2)]. (Л.15)
В формулах (Л.14) и (Л.15) обозначено:
t и h - толщина и высота стенки соответственно;
Af - площадь сечения пояса балки;
τcr, μ - критическое напряжение и отношение размеров отсеков стенки соответственно, определяемые согласно 9.5.3;
β - коэффициент, вычисляемый по формуле
β = 0,1 + 3α ≥ 0,15. (Л.16)
Здесь α = 8Wmin(h2 + a2)/(th2a2) ≤ 0,1;
Wmin - минимальный момент сопротивления таврового
сечения, состоящего из сжатого пояса балки и примыкающего к нему участка стенки
высотой ![]() (относительно собственной
оси тавра, параллельной поясу балки);
(относительно собственной
оси тавра, параллельной поясу балки);
a - шаг ребер жесткости.
Рисунок Л.1 - Схема балки с гибкой стенкой
Л.4.9 Поперечные ребра жесткости, сечение которых принимают не менее указанных в Л.4.8, рассчитывают на устойчивость как стержни, сжатые силой N, определяемой по формуле
N = 3,3Rsγcthβμ(1 - τcr/Rs)/(1 + μ2), (Л.17)
где все обозначения принимают по Л.4.8.
Значение N принимают равным не менее значения сосредоточенной нагрузки, расположенной над ребром.
Расчетную длину стержня принимают равной lef = h(1 - β), но не менее 0,7h.
Симметричное двустороннее ребро рассчитывают на центральное сжатие, одностороннее - на внецентренное сжатие с эксцентриситетом, равным расстоянию от оси стенки до центра тяжести расчетного сечения стержня.
В расчетное сечение стержня включают сечение ребра жесткости и
полосы стенки шириной ![]() с каждой стороны ребра.
с каждой стороны ребра.
Л.4.10 Размеры сечений двутавровых балок с гибкой стенкой с ребрами, удовлетворяющие условию (Л.14), определяют по формулам:
tw =
(0,19 + 29Ry/E)B; hw = tw![]() v/γc; bf = 0,76hw/
v/γc; bf = 0,76hw/![]() ; tf = tw
; tf = tw![]() , (Л.18)
, (Л.18)
где ![]() = 12,9 - 2060Ry/E.
= 12,9 - 2060Ry/E.
Эффективное значение расчетного сопротивления стали Ry,ef определяют по формуле
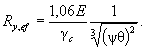 (Л.19)
(Л.19)
С целью удовлетворения условия (Л.15) при необходимости увеличивают количество ребер жесткости или толщину стенки в отсеках балки, расположенных у опор.
При выборе стали выполняют условие Ry ≤ Ry,ef.
Л.4.11 В балках по Л.4.1 с
условной гибкостью стенки 7 ≤
![]() ≤ 10 при действии
равномерно распределенной нагрузки или при числе сосредоточенных одинаковых
нагрузок в пролете 5 и более, расположенных на
равных расстояниях друг от друга и от опор, допускается не укреплять стенку в
пролете поперечными ребрами по рисунку Л.1,
при этом нагрузка должна быть приложена симметрично относительно плоскости
стенки.
≤ 10 при действии
равномерно распределенной нагрузки или при числе сосредоточенных одинаковых
нагрузок в пролете 5 и более, расположенных на
равных расстояниях друг от друга и от опор, допускается не укреплять стенку в
пролете поперечными ребрами по рисунку Л.1,
при этом нагрузка должна быть приложена симметрично относительно плоскости
стенки.
Прочность таких балок проверяют по формуле
![]() (Л.20)
(Л.20)
где δ - коэффициент, учитывающий влияние поперечной силы на несущую способность балки и определяемый по формуле
δ = 1 - 5,6Afh/(Awl).
При этом принимают tf = (2 - 3)tw и 0,025 ≤ Afh/(Awt) ≤ 0,04.
Л.4.12 Высоту стенки двутавровых балок минимального сечения с гибкой стенкой без ребер определяют из условия
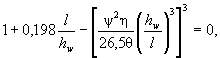 (Л.21)
(Л.21)
где η = 0,72 - hw/l + 0,13l/hw.
Эффективное значение расчетного сопротивления стали Ry,ef определяют по формуле
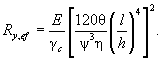 (Л.22)
(Л.22)
Для балок минимального сечения из стали с другим расчетным сопротивлением Ry (Ry < Ry,ef) высоту стенки балки определяют из условия
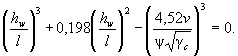 (Л.23)
(Л.23)
Размеры двутавровых балок минимального сечения с гибкой стенкой без ребер определяют по формулам:
![]()
![]()
![]() (Л.24)
(Л.24)
где αf = 0,025l/hw.
Л.5 БАЛКИ С ПЕРФОРИРОВАННОЙ СТЕНКОЙ
Л.5.1 Балки с перфорированной стенкой проектируют из прокатных двутавровых балок, как правило, из стали с пределом текучести до 440 Н/мм2.
Сварные соединения стенок выполняют стыковым швом с полным проваром.
Л.5.2 Расчет на прочность балок, изгибаемых в плоскости стенки (рисунок Л.2), выполняют по формулам:
![]() (Л.25)
(Л.25)
![]() (Л.26)
(Л.26)
![]() (Л.27)
(Л.27)
где M - изгибающий момент в сечении балки;
Q - поперечная сила в сечении балки;
Qs - то же, на расстоянии (c + s - 0,5a) от опоры (рисунок Л.2);
Wx - момент сопротивления сечения балки с отверстием относительно оси x-x;
W1,max, W1,min - наибольший и наименьший моменты сопротивления таврового сечения;
ξ = d/h.
Л.5.3 Расчет на устойчивость балок выполняют согласно требованиям 9.4.1; при этом геометрические характеристики вычисляют для сечения с отверстием.
Устойчивость балок считают обеспеченной, если выполняются требования 9.4.4 и 9.4.5.
Л.5.4 В опорных сечениях стенку балок при hef/t > 40 укрепляют ребрами жесткости и рассчитывают согласно требованиям 9.5.13; при этом у опорного сечения принимают c ≥ 250 мм (рисунок Л.2).
Л.5.5 В сечениях балки при отношении hef/t > ![]() или при невыполнении требований 9.2.2 устанавливают ребра жесткости в
соответствии с требованиями 9.5.9.
или при невыполнении требований 9.2.2 устанавливают ребра жесткости в
соответствии с требованиями 9.5.9.
Сосредоточенные грузы располагают только в сечениях балки, не ослабленных отверстиями.
Высота стенки сжатого таврового сечения должна удовлетворять
требованиям таблицы 8, в формуле (6) которой принимают ![]() .
.
Л.5.6 При определении прогиба балок с отношением l/hef ≥ 12 (где l - пролет балки) момент инерции сечения балки с отверстием умножают на коэффициент 0,95.
Рисунок Л.2 - Схема участка балки с перфорированной стенкой
ПРИЛОЖЕНИЕ М
(рекомендуемое)
КОЭФФИЦИЕНТ УСТОЙЧИВОСТИ ПРИ ИЗГИБЕ φb
М.1 Коэффициент φb для расчета на устойчивость изгибаемых элементов двутаврового, таврового и швеллерного сечений определяют в зависимости от расстановки связей, раскрепляющих сжатый пояс, вида нагрузки и места ее приложения. При этом предполагается, что нагрузка действует в плоскости наибольшей жесткости (Ix > Iy), а опорные сечения закреплены от боковых смещений и поворота.
М.2 Для балки и консоли двутаврового сечения с двумя осями симметрии коэффициент φb принимают равным:
при φ1 ≤ 0,85
φb = φ1; (М.1)
при φ1 > 0,85
φb = 0,68 + 0,21φ1 ≤ 1, (М.2)
где значение φ1 вычисляют по формуле
В формуле (М.3) обозначено:
ψ - коэффициент, вычисляемый согласно требованиям М.3;
h - полная высота сечения прокатного двутавра или расстояние между осями поясов (пакетов поясных листов) составного двутавра;
lef - расчетная длина балки или консоли, определяемая согласно требованиям 9.4.2.
М.3 Значение коэффициента ψ в формуле (М.3) вычисляют по формулам таблиц (М.1) и (М.2) в зависимости от количества закреплений сжатого пояса, вида нагрузки и места ее приложения, а также от коэффициента α, равного:
а) для прокатных двутавров
где It - момент инерции при свободном кручении, определяемый согласно приложению И;
h - полная высота сечения;
Таблица М.1 - Коэффициент ψ для балок двутаврового сечения с двумя осями симметрии
|
Вид нагрузки в пролете |
Эпюра Mx на участке lef |
Пояс, к которому приложена нагрузка |
Коэффициент ψ при значениях α |
||
|
0,1 ≤ α ≤ 40 |
40 < α ≤ 400 |
||||
|
Без закреплений |
Сосредоточенная |
|
Сжатый |
1,75 + 0,09α |
3,3 + 0,053α - 4,5 · 10-5α2 |
|
Растянутый |
5,05 + 0,09α |
6,6 + 0,053α - 4,5 · 10-5α2 |
|||
|
Равномерно распределенная |
|
Сжатый |
1,60 + 0,08α |
3,15 + 0,04α - 2,7 · 10-5α2 |
|
|
Растянутый |
3,80 + 0,08α |
5,35 + 0,04α - 2,7 · 10-5α2 |
|||
|
Два и более, делящие пролет на равные части |
Любая |
|
Любой |
2,25 + 0,07α |
3,6 + 0,04α - 3,5 · 10-5α2 |
|
Одно в середине |
Сосредоточенная в середине |
|
Любой |
1,75ψ1 |
|
|
Сосредоточенная в четверти |
|
Сжатый |
1,14ψ1 |
||
|
Растянутый |
1,60ψ1 |
||||
|
Равномерно распределенная |
|
Сжатый |
1,14ψ1 |
||
|
Растянутый |
1,30ψ1 |
||||
|
Примечание - Значение ψ1 принимают равным ψ при двух и более закреплениях сжатого пояса в пролете. |
|||||
Таблица М.2 - Коэффициент ψ для жестко заделанных консолей двутаврового сечения с двумя осями симметрии
|
Пояс, к которому приложена нагрузка |
Коэффициент ψ при отсутствии закреплений сжатого пояса и при значениях α |
||
|
4 ≤ α ≤ 28 |
28 < α ≤ 100 |
||
|
Сосредоточенная на конце консоли |
Растянутый |
1,0 + 0,16α |
4,0 + 0,05α |
|
Сжатый |
6,2 + 0,08α |
7,0 + 0,05α |
|
|
Равномерно распределенная |
Растянутый |
1,42√α |
|
б) для составных двутавров из листов со сварными или фрикционными поясными соединениями
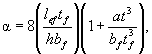 (М.5)
(М.5)
где обозначено:
для сварных двутавров из трех листов:
tf и bf - толщина и ширина пояса балки;
h - расстояние между осями поясов;
a = 0,5h;
t - толщина стенки (t = tw);
для составных двутавров с фрикционными поясными соединениями:
tf - суммарная толщина листов пояса и полки поясного уголка;
bf - ширина листов пояса;
h - расстояние между осями пакетов поясных листов;
a - ширина вертикальной полки поясного уголка за вычетом толщины его полки;
t - суммарная толщина стенки и вертикальных полок поясных уголков.
Если на участке балки lef эпюра Mx по своему очертанию отличается от приведенных в таблице М.1, то допускается значение ψ определять по формулам для наиболее близкой по очертанию эпюры Mx, в которую может быть вписана фактическая эпюра.
В случаях когда у консоли сжатый пояс закреплен от бокового перемещения в конце или по ее длине, значение ψ допускается принимать равным:
при сосредоточенной нагрузке, приложенной к растянутому поясу на конце консоли, ψ = 1,75ψ1, где значение ψ1 принимают согласно примечанию к таблице М.1;
в остальных случаях - как для консоли без закреплений.
М.4 Для разрезной балки двутаврового сечения с одной осью симметрии (рисунок М.1) коэффициент φb определяют по таблице М.3, где значения φ1, φ2 и n вычисляют по формулам:
![]() (М.7)
(М.7)
В формулах (М.6) - (М.8) обозначено:
ψa - коэффициент, вычисляемый по формуле
ψa = (B + ![]() )D; (М.9)
)D; (М.9)
h - расстояние между осями поясов;
h1 и h2 - расстояние от центра тяжести сечения до оси соответственно более развитого и менее развитого поясов;
lef - расчетная длина балки, определяемая согласно требованиям 9.4.2;
I1 и I2 - моменты инерции сечения более развитого и менее развитого поясов относительно оси симметрии сечения балки соответственно.
Рисунок М.1 - Схема двутаврового сечения с одной осью симметрии
Таблица М.3 - Коэффициент φb
|
Коэффициент φb при значении φ2 |
||
|
до 0,85 |
св. 0,85 |
|
|
Более развитый |
φ1 ≤ 1 |
φ1[0,21 + 0,68(n/φ1 + (1 - n)/φ2)] ≤ 1 |
|
Менее развитый |
φ2 |
0,68 + 0,21φ2 ≤ 1 |
М.5 Значения B, C и D в формуле (М.9) определяют по таблицам М.4 и М.5 в зависимости от коэффициентов:
δ = n + 0,734β; (М.10)
μ = n + 1,145β; (М.11)
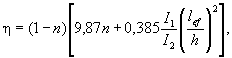 (М.13)
(М.13)
где значения n, b1, h, I2, lef принимают согласно настоящему приложению, а I1 - согласно приложению И.
Коэффициент α в табл. М.5 определяют по формуле (М.4).
Таблица М.4 - Коэффициент В
|
Коэффициент B при нагрузке |
|||
|
сосредоточенной в середине пролета |
равномерно распределенной |
вызывающей чистый изгиб |
|
|
|
δ |
μ |
β |
|
|
δ - 1 |
μ - 1 |
β |
|
|
1 - δ |
1 - μ |
-β |
|
|
-δ |
-μ |
-β |
Таблица М.5 - Коэффициенты C и D
|
Коэффициент C при сечении |
Коэффициент D |
||
|
двутавровом (n ≤ 0,9) |
тавровом (n = 1,0) |
||
|
Сосредоточенная в середине пролета |
0,330η |
0,0826α |
3,265 |
|
Равномерно распределенная |
0,481η |
0,1202α |
2,247 |
|
Вызывающая чистый изгиб |
0,101η |
0,0253α |
4,315 |
М.6 Для двутаврового сечения при 0,9 < п < 1,0 коэффициент ψa определяют линейной интерполяцией между значениями, полученными по формуле (М.9) для двутаврового сечения при n = 0,9 и для таврового при n = 1.
Для таврового сечения при сосредоточенной или равномерно распределенной нагрузке и α < 40 коэффициенты ψa умножают на (0,8 + 0,004α).
В балках с менее развитым сжатым поясом при n > 0,7 и 5 ≤ lef/b2 ≤ 25 значение коэффициента φ2 необходимо уменьшить умножением на (1,025 - 0,015lef/b2) и принимать при этом не более 0,95. Значения lef/b2 > 25 в таких балках не допускаются.
М.7 Для балки швеллерного сечения коэффициент φb допускается принимать φb = 0,7φ1, где φ1 определяют как для балок двоякосимметричного двутаврового сечения, используя формулы (М.3), (М.4), где значения Ix, Iy, It принимают для швеллера.
ПРИЛОЖЕНИЕ Н
(рекомендуемое)
УСТОЙЧИВОСТЬ СТЕНОК БАЛОК, УКРЕПЛЕННЫХ ПРОДОЛЬНЫМИ И ПРОМЕЖУТОЧНЫМИ РЕБРАМИ ЖЕСТКОСТИ
Н.1 В стенке балки симметричного двутаврового сечения 1-го класса, укрепленной кроме поперечных ребер жесткости одним продольным ребром жесткости, расположенным на расстоянии h1 от расчетной (сжатой) границы отсека (рисунок Н.1), обе пластинки, на которые это ребро разделяет отсек, рассчитывают отдельно:
а) пластинку 1, расположенную между сжатым поясом и продольным ребром, - по формуле
где ![]()
![]()
σ, σloc, τ - определяют согласно требованиям 9.5.2;
σcr,1, σloc,cr,1 - определяют по формулам:
при σloc = 0
где ![]()
при σloc ≠ 0 и μ1 = a/h1 ≤ 2 (при μ1 > 2 принимают μ1 = 2)
где ψ = (μ1 + 1/μ1)2 и ![]()
критическое напряжение τcr,1 определяют по формуле (72) с подстановкой в нее размеров проверяемой пластинки;
а - балка с сжатым верхним поясом; б - балка с растянутым верхним поясом; 1, 2 - пластинки
Рисунок Н.1 - Схема балки, укрепленной поперечными (3) и продольными (4) ребрами жесткости
б) пластинку 2, расположенную между продольным ребром и растянутым поясом, - по формуле
где σ и τ - напряжения, определяемые согласно 5.22;
σloc,2 - напряжение, принимаемое равным в зависимости от того, к какому поясу приложена нагрузка:
к сжатому (см. черт. Н.1, а) - σloc,2 = 0,4σloc (здесь σloc определяют согласно 9.5.2);
к растянутому (рисунок Н.1, б) - σloc,2 = σloc;
σloc,cr,2 - напряжение, определяемое по формуле (71), где c1 и c2 определяют соответственно по таблице 8 при ρ = 0,4 и по таблице 9 при δ = 1, заменяя значение hef значением (hef - h1);
τcr,2 - напряжение, определяемое по формуле (72) с подстановкой в нее размеров проверяемой пластинки.
Н.2 При укреплении пластинки 1, расположенной между сжатым поясом и продольным ребром, промежуточными ребрами их доводят до продольного ребра (рисунок Н.2).
В этом случае расчет пластинки 1 выполняют по формулам (Н.1) - (Н.4), в которых за величину a принимают a1 - расстояние между осями соседних промежуточных ребер (рисунок Н.2). Расчет пластинки 2 выполняют согласно требованиям Н.1, б.
Н.3 Расчет на устойчивость
стенок балок асимметричного сечения (с более развитым сжатым поясом), укрепленных
поперечными ребрами и одним продольным ребром, расположенным в сжатой зоне,
выполняют по формулам (Н.1) и (Н.2); при этом в формулы (Н.2), (Н.3) и (Н.5)
вместо отношения h1/hef подставляют ![]() , а в формулу (Н.6)
вместо (0,5
- h1/hef) подставляют [σ1/(σ1 - σ2) - h1/hef], где σ2 - краевое растягивающее растяжение (со знаком «минус») у
расчетной границы отсека.
, а в формулу (Н.6)
вместо (0,5
- h1/hef) подставляют [σ1/(σ1 - σ2) - h1/hef], где σ2 - краевое растягивающее растяжение (со знаком «минус») у
расчетной границы отсека.
Н.4 При укреплении стенки поперечными и одним продольным ребрами жесткости моменты инерции сечения этих ребер Ir и Irl соответственно должны удовлетворять требованиям 9.5.9 и формулы
Ir ≥ 3heftw3, (Н.7)
а также таблицы Н.1.
При расположении поперечных и продольных ребер жесткости с одной стороны стенки моменты инерции сечения каждого из них вычисляют относительно оси, совпадающей с ближайшей к ребру гранью стенки.
Рисунок Н.2 - Схема балки, укрепленной поперечными (3), продольными (4) и промежуточными (5) ребрами жесткости
Таблица Н.1
|
h1/hef |
Значение Irl продольного ребра |
||
|
требуемое |
предельное |
||
|
минимальное |
максимальное |
||
|
0,20 |
(2,5 - 0,5a/hef)a2tw3/hef |
1,5heftw3 |
7heftw3 |
|
0,25 |
(1,5 - 0,4a/hef)a2tw3/hef |
1,5heftw3 |
8,5heftw3 |
|
0,30 |
1,5heftw3 |
- |
- |
|
Примечание - При вычислении Irl для промежуточных значений h1/hef допускается линейная интерполяция. |
|||
ПРИЛОЖЕНИЕ О
(рекомендуемое)
РАСЧЕТНЫЕ ДЛИНЫ КОЛОНН И СТОЕК
Таблица О.1 - Расчетная длина элемента, раскрепленного связями в одной плоскости
|
Схемы элемента в плоскости связей (а) и из плоскости связей (б) |
Расчетные длины в плоскости связей lef и из плоскости lef,1 |
|
|
lef = (0,83 + 0,17α3)l ≥ 0,8l; (О.1)
|
|
|
|
|
Обозначение, принятые в таблице О.1: k - число участков равной длины;
где Nmax - наибольшее усилие сжатия (действует на крайнем участке); N2 - усилие на участке, примыкающем к участку с Nmax; ΣNi - сумма усилий на всех участках, кроме Nmax. Примечания 1 Растягивающие усилия учитывают со знаком «минус». 2 Расчет на устойчивость из плоскости связей выполняют на усилие Nmax. |
|
Таблица О.2 - Коэффициент расчетной длины μ колонны (стоек) с упругим закреплением концов
|
μ |
|
|
|
|
|
|
|
|
|
При 0 ≤ α ≤ ∞ и β ≤ 9,87
при α = 0 и β > 9,87 μ = 1 |
|
Обозначения, принятые в таблице О.2:
где Km - коэффициент жесткости упругого закрепления, Н/см, равный значению реактивного момента, возникающего в опорном сечении при его повороте на угол φ = 1; Kn - коэффициент жесткости упругой опоры, Н/см, равный значению реактивной силы, возникающей в опорном сечении при его смещении на δ = 1. Примечание - Значения Km и Kn для некоторых рамных систем приведены в таблице О.3. |
|
Таблица О.3 - Коэффициенты жесткости Km и Kn для колонн (стоек) рамных систем
|
Формула для схемы по таблице О.2 |
Значения Km и Kn |
|
|
|
(О.5) |
Km = 0;
|
|
|
(О.5) |
Kn = ∞ |
|
|
(О.5) |
Kn = ∞ |
|
|
(О.6) |
|
|
|
(О.7) |
Kn = ∞ |
|
|
(О.7) |
Kn = ∞ |
Таблица О.4 - Коэффициент расчетной длины μ колонн однопролетных и многопролетных рам
|
n |
μ |
|
|
|
0 |
2,0 |
|
|
От 0,03 до 0,2 |
|
|
Св. 0,2 |
|
|
|
|
От 0,03 до 0,2 |
|
|
Св. 0,2 |
|
|
|
|
n |
|
|
|
n |
|
|
Обозначение, принятое в таблице О.4:
Примечание - Значения μ для колонн многоэтажных рам приведены для нижнего этажа. |
||
О.1 РАСЧЕТНАЯ ДЛИНА КОЛОНН С УЧЕТОМ ВЛИЯНИЯ ХАРАКТЕРА ДЕФОРМИРОВАНИЯ СИСТЕМЫ ПОД НАГРУЗКОЙ
Коэффициент расчетной длины μ, определенный согласно 11.2.8 и 11.2.9 для колонн свободных одноэтажных (при отсутствии жесткого диска покрытия) и многоэтажных рам, допускается уменьшать умножением на коэффициент ψ, определяемый по формуле
ψ = 1 - α[1 - (ω/5)2]5/4, (О.14)
где α = 0,65 - 0,9β + 0,25β2;
![]()
Здесь обозначено:
β = 1 - M1/M ≤ 0,2;
m = MA/(NWc);
![]() - условная гибкость колонны, вычисленная с
учетом требований 11.2.8, 11.2.9.
- условная гибкость колонны, вычисленная с
учетом требований 11.2.8, 11.2.9.
Расчетные значения продольной силы N и изгибающего момента M в рассчитываемой свободной раме определяют согласно требованиям 10.2.3.
Значение изгибающего момента M1 определяют для того же сочетания нагрузок в том же сечении колонны, где действует момент M, рассматривая раму в данном расчетном случае как несвободную.
ПРИЛОЖЕНИЕ П
(справочное)
КОЭФФИЦИЕНТ РАСЧЕТНОЙ ДЛИНЫ μ УЧАСТКОВ СТУПЕНЧАТЫХ КОЛОНН
П.1 Коэффициент расчетной длины μ1 для защемленного в основании нижнего участка одноступенчатой колонны принимают:
при верхнем конце колонн, свободном от закреплений, - по таблице П.1;
при закреплении верхнего конца от поворота по возможности его свободного смещения - по таблице П.2;
при закреплении верхнего конца от смещения - по формуле
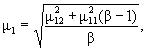 (П.1)
(П.1)
где μ12 и μ11 - коэффициенты расчетной длины нижнего участка колонны при нагрузках F1 = 0 и F2 = 0 соответственно, определяемые при шарнирном опирании верхнего конца по таблице П.3, а при закреплении от поворота - по таблице П.4.
В таблицах П.1 - П.4 обозначено:
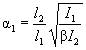 и
и ![]()
где I1, I2, l1, l2 - моменты инерции сечений и длины нижнего и верхнего участков колонны соответственно;
β = (F1 + F2)/F2.
П.2 Коэффициент расчетной длины μ2 для верхнего участка одноступенчатой колонны во всех случаях определяют по формуле
μ2 = μ1/α1 ≤ 3. (П.2)
П.3 Коэффициент расчетной длины μ1 для защемленного в основании нижнего участка двухступенчатой колонны (рисунок П.1, а) при условиях закрепления верхнего конца, указанных в таблице П.5, определяют по формуле
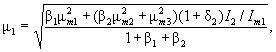 (П.3)
(П.3)
где β1 = F1/F3; β2 = F2/F3; δ2 = l2/l1;
μm1, μm2, μm3 - коэффициенты, определяемые по таблице П.5 как для одноступенчатых колонн по условным схемам (рисунок П.1, б, в, г);
Im1 = (I1l1 + I2l2)/(l1 + l2) - приведенное значение момента инерции сечения участка длиной (l1 + l2).
Здесь F1, F2, F3 - продольные силы, приложенные к верху нижнего, среднего и верхнего участков колонн с моментами инерции I1, I2, I3 и длинами l1, l2, l3 соответственно.
Приведенное значение момента инерции сечения участка длиной (l2 + l3) на рисунке П.1, б определяют по формуле
Im2 = (I2l2 + I3l3)/(l2 + l3).
П.4 Коэффициенты расчетной длины μ2 для среднего участка двухступенчатой колонны длиной l2 и μ3 для верхнего участка колонны длиной l3 определяют по формулам:
μ2 = μ1/α2; (П.4)
μ3 = μ1/α3 ≤ 3, (П.5)
где 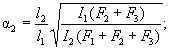
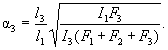
Рисунок П.1 - Схема двухступенчатой колонны (а) и условные схемы загружений при приложении сил F1, F2 и F3 к нижнему (б), среднему (в) и верхнему (г) участкам соответственно
Таблица П.1 - Коэффициент расчетной длины μ1 для одноступенчатых колонн с верхним концом, свободным от закреплений
|
Расчетная схема |
α1 |
Коэффициент μ1 при значении n |
|||||||||||||||||||
|
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
1,2 |
1,4 |
1,6 |
1,8 |
2,0 |
2,5 |
5,0 |
10,0 |
20,0 |
||
|
|
0 |
2,0 |
2,0 |
2,0 |
2,0 |
2,0 |
2,0 |
2,0 |
2,0 |
2,0 |
2,0 |
2,0 |
2,0 |
2,0 |
2,0 |
2,0 |
2,0 |
2,0 |
2,0 |
2,0 |
2,0 |
|
0,2 |
2,0 |
2,01 |
2,02 |
2,03 |
2,04 |
2,05 |
2,06 |
2,06 |
2,07 |
2,08 |
2,09 |
2,10 |
2,12 |
2,14 |
2,15 |
2,17 |
2,21 |
2,40 |
2,76 |
3,38 |
|
|
0,4 |
2,0 |
2,04 |
2,08 |
2,11 |
2,23 |
2,18 |
2,21 |
2,25 |
2,28 |
2,32 |
2,35 |
2,42 |
2,48 |
2,54 |
2,60 |
2,66 |
2,80 |
- |
- |
- |
|
|
0,6 |
2,0 |
2,11 |
2,20 |
2,28 |
2,36 |
2,44 |
2,52 |
2,59 |
2,66 |
2,73 |
2,80 |
2,93 |
3,05 |
3,17 |
3,28 |
3,39 |
- |
- |
- |
- |
|
|
0,8 |
2,0 |
2,25 |
2,42 |
2,56 |
2,70 |
2,83 |
2,96 |
3,07 |
3,17 |
3,27 |
3,36 |
3,55 |
3,74 |
- |
- |
- |
- |
- |
- |
- |
|
|
1,0 |
2,0 |
2,50 |
2,73 |
2,94 |
3,13 |
3,29 |
3,44 |
3,59 |
3,74 |
3,87 |
4,0 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
|
1,5 |
3,0 |
3,43 |
3,77 |
4,07 |
4,35 |
4,61 |
4,86 |
5,05 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
|
2,0 |
4,0 |
4,44 |
4,90 |
5,29 |
5,67 |
6,03 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
|
2,5 |
5,0 |
5,55 |
6,08 |
6,56 |
7,00 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
|
3,0 |
6,0 |
6,65 |
7,25 |
7,82 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
Таблица П.2 - Коэффициент расчетной длины μ1 для одноступенчатых колонн с верхним концом, закрепленным только от поворота
|
α1 |
Коэффициент μ1 при значении n |
||||||||||||||||||||
|
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
1,2 |
1,4 |
1,6 |
1,8 |
2,0 |
2,5 |
5,0 |
10,0 |
20,0 |
||
|
|
0 |
2,0 |
1,92 |
1,86 |
1,80 |
1,76 |
1,70 |
1,67 |
1,64 |
1,60 |
1,57 |
1,55 |
1,50 |
1,46 |
1,43 |
1,40 |
1,37 |
1,32 |
1,18 |
1,10 |
1,05 |
|
0,2 |
2,0 |
1,93 |
1,87 |
1,82 |
1,76 |
1,71 |
1,68 |
1,64 |
1,62 |
1,59 |
1,56 |
1,52 |
1,48 |
1,45 |
1,41 |
1,39 |
1,33 |
1,20 |
1,11 |
- |
|
|
0,4 |
2,0 |
1,94 |
1,88 |
1,83 |
1,77 |
1,75 |
1,72 |
1,69 |
1,66 |
1,62 |
1,61 |
1,57 |
1,53 |
1,50 |
1,48 |
1,45 |
1,40 |
- |
- |
- |
|
|
0,6 |
2,0 |
1,95 |
1,91 |
1,86 |
1,83 |
1,79 |
1,77 |
1,76 |
1,72 |
1,71 |
1,69 |
1,66 |
1,63 |
1,61 |
1,59 |
- |
- |
- |
- |
- |
|
|
0,8 |
2,0 |
1,97 |
1,94 |
1,92 |
1,90 |
1,88 |
1,87 |
1,86 |
1,85 |
1,83 |
1,82 |
1,80 |
1,79 |
- |
- |
- |
- |
- |
- |
- |
|
|
1,0 |
2,0 |
2,00 |
2,00 |
2,00 |
2,00 |
2,00 |
2,00 |
2,00 |
2,00 |
2,00 |
2,00 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
|
1,5 |
2,0 |
2,12 |
2,25 |
2,33 |
2,38 |
2,43 |
2,48 |
2,52 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
|
2,0 |
2,0 |
2,45 |
2,66 |
2,81 |
2,91 |
3,00 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
|
2,5 |
2,5 |
2,94 |
3,17 |
3,34 |
3,50 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
|
3,0 |
3,0 |
3,43 |
3,70 |
3,93 |
4,12 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
Таблица П.3 - Коэффициенты расчетной длины μ12 и μ11 для одноступенчатых колонн с неподвижным шарнирно опертым верхним концом
|
I2/I1 |
Коэффициенты μ12 и μ11 при l2/l1 |
|||||||||||||||
|
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
1,2 |
1,4 |
1,6 |
1,8 |
2,0 |
||
|
|
|
|
|
|
|
|
Коэффициент μ12 |
|
|
|
|
|
|
|||
|
0,04 |
1,02 |
1,84 |
2,25 |
2,59 |
2,85 |
3,08 |
3,24 |
3,42 |
3,70 |
4,00 |
4,55 |
5,25 |
5,80 |
6,55 |
7,20 |
|
|
0,06 |
0,91 |
1,47 |
1,93 |
2,26 |
2,57 |
2,74 |
3,05 |
3,05 |
3,24 |
3,45 |
3,88 |
4,43 |
4,90 |
5,43 |
5,94 |
|
|
0,08 |
0,86 |
1,31 |
1,73 |
2,05 |
2,31 |
2,49 |
2,68 |
2,85 |
3,00 |
3,14 |
3,53 |
3,93 |
4,37 |
4,85 |
5,28 |
|
|
0,1 |
0,83 |
1,21 |
1,57 |
1,95 |
2,14 |
2,33 |
2,46 |
2,60 |
2,76 |
2,91 |
3,28 |
3,61 |
4,03 |
4,43 |
4,85 |
|
|
0,2 |
0,79 |
0,98 |
1,23 |
1,46 |
1,67 |
1,85 |
2,02 |
2,15 |
2,28 |
2,40 |
2,67 |
2,88 |
3,11 |
3,42 |
3,71 |
|
|
0,3 |
0,78 |
0,90 |
1,09 |
1,27 |
1,44 |
1,60 |
1,74 |
1,86 |
1,98 |
2,11 |
2,35 |
2,51 |
2,76 |
2,99 |
3,25 |
|
|
0,4 |
0,78 |
0,88 |
1,02 |
1,17 |
1,32 |
1,45 |
1,58 |
1,69 |
1,81 |
1,92 |
2,14 |
2,31 |
2,51 |
2,68 |
2,88 |
|
|
0,5 |
0,78 |
0,86 |
0,99 |
1,10 |
1,22 |
1,35 |
1,47 |
1,57 |
1,67 |
1,76 |
1,96 |
2,15 |
2,34 |
2,50 |
2,76 |
|
|
1,0 |
0,78 |
0,85 |
0,92 |
0,99 |
1,06 |
1,13 |
1,20 |
1,27 |
1,34 |
1,41 |
1,54 |
1,68 |
1,82 |
1,97 |
2,10 |
|
|
|
|
|
|
|
|
|
Коэффициент μ11 |
|
|
|
|
|
|
|||
|
0,04 |
0,67 |
0,67 |
0,83 |
1,25 |
1,43 |
1,55 |
1,65 |
1,70 |
1,75 |
1,78 |
1,84 |
1,87 |
1,88 |
1,90 |
1,92 |
|
|
0,06 |
0,67 |
0,67 |
0,81 |
1,07 |
1,27 |
1,41 |
1,51 |
1,60 |
1,64 |
1,70 |
1,78 |
1,82 |
1,84 |
1,87 |
1,88 |
|
|
0,08 |
0,67 |
0,67 |
0,75 |
0,98 |
1,19 |
1,32 |
1,43 |
1,51 |
1,58 |
1,63 |
1,72 |
1,77 |
1,81 |
1,82 |
1,84 |
|
|
0,1 |
0,67 |
0,67 |
0,73 |
0,93 |
1,11 |
1,25 |
1,36 |
1,45 |
1,52 |
1,57 |
1,66 |
1,72 |
1,77 |
1,80 |
1,82 |
|
|
0,2 |
0,67 |
0,67 |
0,69 |
0,75 |
0,89 |
1,02 |
1,12 |
1,21 |
1,29 |
1,36 |
1,46 |
1,54 |
1,60 |
1,65 |
1,69 |
|
|
0,3 |
0,67 |
0,67 |
0,67 |
0,71 |
0,80 |
0,90 |
0,99 |
1,08 |
1,15 |
1,22 |
1,33 |
1,41 |
1,48 |
1,54 |
1,59 |
|
|
0,4 |
0,67 |
0,67 |
0,67 |
0,69 |
0,75 |
0,84 |
0,92 |
1,00 |
1,07 |
1,13 |
1,24 |
1,33 |
1,40 |
1,47 |
1,51 |
|
|
0,5 |
0,67 |
0,67 |
0,67 |
0,69 |
0,73 |
0,81 |
0,87 |
0,94 |
1,01 |
1,07 |
1,17 |
1,26 |
1,33 |
1,39 |
1,44 |
|
|
1,0 |
0,67 |
0,67 |
0,67 |
0,68 |
0,71 |
0,74 |
0,78 |
0,82 |
0,87 |
0,91 |
0,99 |
1,07 |
1,13 |
1,19 |
1,24 |
|
Таблица П.4 - Коэффициенты расчетной длины μ12 и μ11 для одноступенчатых колонн с неподвижным верхним концом, закрепленным от поворота
|
I2/I1 |
Коэффициенты μ12 и μ11 при l2/l1 |
|||||||||||||||
|
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
1,2 |
1,4 |
1,6 |
1,8 |
2,0 |
||
|
|
Коэффициент μ12 |
|||||||||||||||
|
0,04 |
0,78 |
1,02 |
1,53 |
1,73 |
2,01 |
2,21 |
2,38 |
2,54 |
2,65 |
2,85 |
3,24 |
3,70 |
4,20 |
4,76 |
5,23 |
|
|
0,06 |
0,70 |
0,86 |
1,23 |
1,47 |
1,73 |
1,93 |
2,08 |
2,23 |
2,38 |
2,49 |
2,81 |
3,17 |
3,50 |
3,92 |
4,30 |
|
|
0,08 |
0,68 |
0,79 |
1,05 |
1,31 |
1,51 |
1,74 |
1,91 |
2,05 |
2,20 |
2,31 |
2,55 |
2,80 |
3,11 |
3,45 |
3,73 |
|
|
0,1 |
0,67 |
0,76 |
1,00 |
1,20 |
1,42 |
1,61 |
1,78 |
1,92 |
2,04 |
2,20 |
2,40 |
2,60 |
2,86 |
3,18 |
3,41 |
|
|
0,2 |
0,64 |
0,70 |
0,79 |
0,93 |
1,07 |
1,23 |
1,41 |
1,50 |
1,60 |
1,72 |
1,92 |
2,11 |
2,28 |
2,45 |
2,64 |
|
|
0,3 |
0,62 |
0,68 |
0,74 |
0,85 |
0,95 |
1,06 |
1,18 |
1,28 |
2,39 |
1,48 |
1,67 |
1,82 |
1,96 |
2,12 |
2,20 |
|
|
0,4 |
0,60 |
0,66 |
0,71 |
0,78 |
0,87 |
0,99 |
1,07 |
1,16 |
1,26 |
1,34 |
1,50 |
1,65 |
1,79 |
1,94 |
2,08 |
|
|
0,5 |
0,59 |
0,65 |
0,70 |
0,77 |
0,82 |
0,93 |
0,99 |
1,08 |
1,17 |
1,23 |
1,39 |
1,53 |
1,66 |
1,79 |
1,92 |
|
|
1,0 |
0,55 |
0,60 |
0,65 |
0,70 |
0,75 |
0,80 |
0,85 |
0,90 |
0,95 |
1,00 |
1,10 |
1,20 |
1,30 |
1,40 |
1,50 |
|
|
|
Коэффициент μ11 |
|||||||||||||||
|
0,04 |
0,66 |
0,68 |
0,75 |
0,94 |
1,08 |
1,24 |
1,37 |
1,47 |
1,55 |
1,64 |
1,72 |
1,78 |
1,81 |
1,85 |
1,89 |
|
|
0,06 |
0,65 |
0,67 |
0,68 |
0,76 |
0,94 |
1,10 |
1,25 |
1,35 |
1,44 |
1,50 |
1,61 |
1,69 |
1,74 |
1,79 |
1,82 |
|
|
0,08 |
0,64 |
0,66 |
0,67 |
0,68 |
0,84 |
1,00 |
1,12 |
1,25 |
1,34 |
1,41 |
1,53 |
1,62 |
1,68 |
1,75 |
1,79 |
|
|
0,1 |
0,64 |
0,65 |
0,65 |
0,65 |
0,78 |
0,92 |
1,05 |
1,15 |
1,25 |
1,33 |
1,45 |
1,55 |
1,62 |
1,68 |
1,71 |
|
|
0,2 |
0,62 |
0,64 |
0,65 |
0,65 |
0,66 |
0,73 |
0,83 |
0,92 |
1,01 |
1,09 |
1,23 |
1,33 |
1,41 |
1,48 |
1,54 |
|
|
0,3 |
0,60 |
0,63 |
0,64 |
0,65 |
0,66 |
0,67 |
0,73 |
0,81 |
0,89 |
0,94 |
1,09 |
1,20 |
1,28 |
1,35 |
1,41 |
|
|
0,4 |
0,58 |
0,63 |
0,63 |
0,64 |
0,64 |
0,66 |
0,68 |
0,75 |
0,82 |
0,88 |
1,01 |
1,10 |
1,19 |
1,26 |
1,32 |
|
|
0,5 |
0,57 |
0,61 |
0,63 |
0,64 |
0,64 |
0,65 |
0,68 |
0,72 |
0,77 |
0,83 |
0,94 |
1,04 |
1,12 |
1,19 |
1,25 |
|
|
1,0 |
0,55 |
0,58 |
0,60 |
0,61 |
0,62 |
0,63 |
0,65 |
0,67 |
0,70 |
0,73 |
0,80 |
0,88 |
0,93 |
1,01 |
1,05 |
|
Таблица П.5 - Коэффициенты μm1, μm2, μm3
|
Значения коэффициентов |
|||
|
μm1 |
μm2 |
μm3 |
|
|
при условной схеме загружения по чертежу |
|||
|
П.1, б |
П.1, в |
П.1, г |
|
|
Свободен от закреплений |
μm1 = 2,0 |
μm2 = 2,0 |
μm3 = μ1 (μ1 - по таблице П.1 при |
|
Закреплен от поворота, допускает смещение |
μm1 = μ1 |
μm2 = μ1 |
μm3 = μ1 (μ1 - по таблице П.2 при |
|
(μ1 - по таблице П.2 при α1 = 0) |
|||
|
Закреплен шарнирно, не допускает смещения |
μm1 = μ11 |
μm2 = μ11 |
μm3 = μ12 (μ12 - по таблице П.3) |
|
(μ11 - по таблице П.3) |
|||
|
Закреплен от поворота и смещения |
μm1 = μ11 |
μm2 = μ11 |
μm3 = μ12 (μ12 - по таблице П.4) |
|
(μ11 - по таблице П.4) |
|||
ПРИЛОЖЕНИЕ Р
(рекомендуемое)
К РАСЧЕТУ ЭЛЕМЕНТОВ НА УСТАЛОСТЬ
Таблица Р.1 - Группы элементов и соединений при расчете на усталость
|
№ п.п. |
Схема элемента и расположение расчетного сечения |
Характеристика элемента |
Группа элемента |
|
1 |
|
Основной металл с прокатными или обработанными механическим путем кромками |
1 |
|
То же, с кромками, обрезанными машинной газовой резкой |
2 |
||
|
2 |
|
Основной металл с обработанными механическим путем кромками при разной ширине и радиусе перехода r, мм: |
|
|
200 |
1 |
||
|
10 |
4 |
||
|
3 |
|
Основной металл во фрикционных соединениях |
1 |
|
4 |
|
Основной металл в болтовом (болты класса точности А) соединении в сечениях по отверстию: |
|
|
а) при парных накладках |
4 |
||
|
б) при односторонних накладках |
5 |
||
|
5 |
|
Переход и закругление (класс чистоты газовой резки 1 или фрезеровка) при α ≥ 72°, r ≥ 0,5b |
2 |
|
6 |
|
Фасонки прямоугольной формы, приваренные встык или втавр к элементам конструкций без механической обработки перехода от фасонки к элементу |
7 |
|
7 |
|
Фасонки, приваренные встык или втавр к стенкам и поясам балок, а также к элементам ферм при α ≤ 45° |
4 |
|
8 |
|
Фасонки прямоугольной или трапециевидной формы, приваренные к поясам балок внахлестку с обваркой по контуру нахлестки без механической обработки швов |
7 |
|
9 |
|
Стыковой необработанный шов; нагрузка перпендикулярна сварному шву; стыкуемые элементы одинаковой ширины и толщины |
2 |
|
10 |
|
Стыковой необработанный шов; стыкуемые элементы разной ширины или разной толщины |
5 |
|
11 |
|
Основной металл в месте перехода к стыковому шву со снятым механическим способом усилением шва: |
|
|
а) при стыковании элементов одинаковой толщины и ширины |
2 |
||
|
б) то же, разной толщины и ширины |
3 |
||
|
12 |
|
Сварные стыковые соединения: |
|
|
листового элемента на подкладном листе (нагрузка перпендикулярна сварному шву) |
4 |
||
|
труб на подкладном кольце |
4 |
||
|
прокатных профилей встык |
4 |
||
|
13 |
|
Сварные сечения двутаврового, таврового и других типов, сваренные непрерывными продольными швами при действии усилия вдоль оси шва |
2 |
|
14 |
|
Элемент со вспомогательным элементом, прикрепленным продольными швами, при α: |
|
|
до 45° |
4 |
||
|
90° |
7 |
||
|
15 |
|
Обрыв поясного листа без механической обработки поперечного (лобового) шва |
7 |
|
16 |
|
Основной металл с поперечным швом; сварной шов двусторонний с плавным переходом к основному металлу |
4 |
|
17 |
|
Основной металл растянутых поясов балок и элементов ферм вблизи диафрагм и ребер, приваренных угловыми швами |
5 |
|
18 |
|
Основной металл в месте перехода к поперечному (лобовому) угловому шву |
6 |
|
19 |
|
Основной металл в соединениях с фланговыми швами (в местах перехода от элемента к концам фланговых швов): |
|
|
а) с двойными фланговыми швами |
8 |
||
|
б) с фланговыми и лобовыми швами |
7 |
||
|
в) при передаче усилия через основной металл |
7 |
||
|
г) щеки анкеров для крепления стальных канатов |
8 |
||
|
20 |
|
Основной металл трубы растянутого раскоса при отношении толщины к наружном диаметру трубы пояса |
|
|
tm/dm ≥ 1/14 |
7 |
||
|
1/20 ≤ tm/dm < 1/14 |
8 |
||
|
21 |
α = 45 - 60° |
Основной металл трубы растянутого раскоса при отношении диаметров раскоса и пояса dd/dm = 0,4 - 0,7 и отношении толщины к наружному диаметру трубы пояса: |
|
|
tm/dm ≥ 1/14 |
6 |
||
|
1/20 ≤ tm/dm < 1/14 |
7 |
||
|
1/35 < tm/dm < 1/20 |
8 |
ПРИЛОЖЕНИЕ С
(рекомендуемое)
УЗЛЫ ФЕРМ С НЕПОСРЕДСТВЕННЫМИ ПРИКРЕПЛЕНИЯМИ ЭЛЕМЕНТОВ РЕШЕТКИ К ПОЯСАМ
С.1 ОБЩИЕ ПОЛОЖЕНИЯ
В узлах ферм с непосредственным прикреплением элементов решетки к поясам проверяют:
несущую способность стенки (полки) пояса, к которой примыкает элемент решетки;
несущую способность элемента решетки вблизи примыкания к поясу;
прочность сварных швов.
В приведенных далее формулах обозначено:
N - усилие в примыкающем элементе (решетки);
M - изгибающий момент от основного воздействия в примыкающем элементе в плоскости фермы в сечении, совпадающем с примыкающей стенкой (полкой) пояса (момент от жесткости узлов допускается не учитывать), для ферм из круглых труб - аналогичный момент в рассматриваемом элементе в сечении, проходящем через точку пересечения этого элемента с образующей пояса;
F - продольная сила в поясе со стороны растянутого элемента решетки;
A - площадь поперечного сечения пояса;
Ry - расчетное сопротивление стали пояса;
t - толщина стенки (полки) пояса;
α - угол примыкания элемента решетки к поясу;
Ad - площадь поперечного сечения элемента решетки;
td - толщина стенки (полки) элемента решетки;
Ryd - расчетное сопротивление стали элемента решетки.
С.2 ФЕРМЫ ИЗ ГНУТОСВАРНЫХ ПРОФИЛЕЙ
С.2.1 Узлы ферм из замкнутых гнутосварных профилей прямоугольного сечения (рисунок С.1) проверяют согласно требованиям С.1, а также учитывают несущую способность боковой стенки пояса (параллельной плоскости узла) в месте примыкания сжатого элемента решетки.
а - K-образный при треугольной решетке; б - то же, при раскосной решетке; в - опорный; г - У-образный
Рисунок С.1 - Узлы ферм из гнутосварных профилей
С.2.2 В случае одностороннего примыкания к поясу двух элементов решетки или более с усилиями разных знаков (рисунок С.1, а, б), а также одного элемента в опорных узлах (рисунок С.1, в) при d/D ≤ 0,9 и g/b ≤ 0,25 несущую способность стенки пояса проверяют для каждого примыкающего элемента по формуле
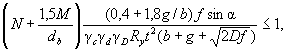 (С.1)
(С.1)
где γd - коэффициент влияния знака усилия в примыкающем элементе, принимаемый равным 1,2 при растяжении и 1 - в остальных случаях;
γD - коэффициент влияния продольной силы в поясе, определяемый при сжатии в поясе, если |F|/(ARy) > 0,5, по формуле
γD = 1,5 - |F|/(ARy),
в остальных случаях γD = 1,0;
b - длина участка линии пересечения примыкающего элемента с поясом в направлении оси пояса, равная db/sin α;
g - половина расстояния между смежными стенками соседних элементов решетки или поперечной стенкой раскоса и опорным ребром;
f = (D - d)/2.
С.2.3 Несущую способность стенки пояса в У-образных узлах (рисунок С.1, г), а также в узлах, указанных в С.2.2, при g/b > 0,25 проверяют по формуле
![]() (С.2)
(С.2)
С.2.4 Несущую способность боковой стенки в плоскости узла в месте примыкания сжатого элемента при d/D > 0,85 проверяют по формуле
N ≤ 2γcγtkRytdb/sin2α, (С.3)
где γt - коэффициент влияния тонкостенности пояса, для отношений Db/t ≥ 25 принимаемый равным 0,8, в остальных случаях - 1;
k - коэффициент, принимаемый равным:
при 4(t/Db)2 - Ry/E ≤ 0 3,6(t/Db)2E/Ry;
при 0 < 4(t/Db)2 - R/E < 6 · 10-4 0,9 + 670(t/Db)2 - 170R/E;
в остальных случаях - 1.
С.2.5 Несущую способность элемента решетки вблизи примыкания к поясу проверяют:
а) в узлах, указанных в С.2.2, при углах примыкания α = 40° - 50° по формуле
где k - определяют, как в С.2.4, но с заменой характеристик пояса на характеристики элемента решетки: Db на большее из значений d или db, t на td и Ry на Ryd.
Для элемента решетки неквадратного сечения в левую часть формулы (С.4) вводят множитель ![]()
б) в узлах, указанных в С.2.3, по формуле
Выражение в круглых скобках формулы (С.5) не должно быть менее 0.
Для элементов решетки неквадратного сечения в левую часть формулы (С.5) вводят множитель (1 + d/db)/2.
С.2.6 Прочность сварных швов, прикрепляющих элементы решетки к поясу, проверяют:
а) в узлах, указанных в С.2.2, при углах примыкания α = 40° - 50° по формуле
![]() (С.6)
(С.6)
где βf, kf, Rwf принимают согласно требованиям раздела 15;
б) в узлах, указанных в С.2.3, по формуле
![]() (С.7)
(С.7)
в) сварные швы, выполненные при наличии установочного зазора, равного (0,5 - 0,7)td, с полным проплавлением стенки профиля рассчитывают как стыковые.
С.3 ФЕРМЫ ИЗ КРУГЛЫХ ТРУБ
С.3.1 Узлы ферм, из круглых труб (рисунок С.2) проверяют согласно требованиям С.1.
а - K-образного типа; б - X-образный; в - опорный
Рисунок С.2 - Узлы ферм из круглых труб (обозначения - см. таблицу С.1)
С.3.2 В случае примыкания к поясу n элементов решетки (рисунок С.2, а, б), а также одного элемента в опорных узлах (рисунок С.2, в) несущую способность стенки пояса проверяют для каждого примыкающего элемента по формулам:
![]() (С.8)
(С.8)
|Nj|sin αj/(ψj2S) ≤ 1, (С.9)
где i - номер примыкающего элемента;
j - номер рассматриваемого примыкающего элемента;
Ni, Nj - усилие в примыкающем элементе, принимаемое с учетом знака («плюс» при растяжении, «минус» при сжатии);
μi - коэффициент, при i = j определяемый по формуле
![]()
при i ≠ j μi = 1;
здесь γdj - - коэффициент влияния знака усилия в рассматриваемом примыкающем элементе, принимаемый равным 0,8 при растяжении и 1,0 - в остальных случаях;
lzj - длина участка примыкания рассматриваемого элемента (для трубчатых элементов lzj = dj/sin αj);
γzj - коэффициент влияния длины примыкания рассматриваемого элемента, для нецилиндрических примыканий определяемый по формуле
![]()
для цилиндрических примыканий (труб) γzj = 1;
bi или bj - ширина примыкающего элемента (для трубчатого элемента bi = di или bj = dj);
S - характеристика несущей способности пояса, определяемая по формуле
S = 13(1 + 0,02δ)t2Ryγc; (С.10)
здесь δ = D/t - тонкостенность пояса;
γDj - коэффициент влияния продольной силы в поясе, определяемый при сжатии в поясе по формуле
γDj = 1 - 0,5(Fj/ARy)2,
в остальных случаях - γDj = 1;
здесь Fj - продольная сила в поясе со стороны растянутого элемента решетки;
γrj - коэффициент влияния подкрепления стенки пояса в узле поперечными ребрами (диафрагмами и т.п.), принимаемый равным 1,25 при расположении подкрепляющего ребра в пределах участка рассматриваемого примыкания и 1 - в остальных случаях;
εij - коэффициент влияния расположения каждого из смежных примыкающих элементов по отношению к рассматриваемому (j-му), определяемый по таблице С.1;
при i = j εij = 1;
ψi = arcsin βwi,
при βi ≤ 0,7 допускается принимать ψi = 1,05βi (βi - см. таблицу С.1), при βi > 0,7
ψi = 1,05βi(1 + 0,15βi8),
βwi = bwi/D;
bwi - ширина охвата пояса примыкающим элементом между кромками сварного шва (при βi ≤ 0,7 допускается принимать βwi = βi, при β > 0,7bwi = bi - tdi).
С.3.3 Несущую способность стенки трубчатых элементов решетки вблизи примыкания к поясу проверяют по формуле
![]() (С.11)
(С.11)
где æ - коэффициент, принимаемый равным: 0,008 - для раскосов в K-образных узлах, при расчете примыканий которых значение коэффициента ζ, определяемого по таблице С.1, составляет менее 0,85; 0,015 - в остальных случаях;
γcd - коэффициент условий работы, принимаемый равным: 0,85 - для элементов, пересекающихся в узле с двумя другими элементами, имеющими разные знаки усилий; 1 - в остальных случаях.
С.3.4 При подкреплении стенки пояса в узле (в местах примыкания рассматриваемого примыкающего элемента) прилегающей и приваренной к поясу накладкой толщиной ta вместо Ry в формуле (С.10) принимают расчетное сопротивление материала накладки Rya, вместо t - приведенную толщину tef, принимаемую равной: для растянутых примыкающих элементов ta, но не более 1,5t; для сжатых - tmax + 0,25tmin, где tmax - большая, а tmin - меньшая из толщин t и ta.
Таблица С.1
|
Расположение оси смежного примыкающего элемента относительно оси рассматриваемого |
Тип узла |
sij |
εij |
|
С той же стороны пояса |
K |
- |
|
|
С противоположной стороны пояса |
X |
0 ≤ sij < D |
|
|
≥ D |
0 |
||
|
Обозначения, принятые в таблице С.1 (рисунок С.2): gij - наименьшее расстояние вдоль оси пояса между сварными швами, прикрепляющими к поясу рассматриваемый и смежный элементы решетки (продольный просвет):
sij - расстояние вдоль пояса между бортами рассматриваемого и смежного примыкающих элементов:
βi = bi/D - отношение ширины примыкания смежного элемента к диаметру пояса (для трубчатых элементов (βi = di/D). Примечание - Значения ζij принимают равными: при gij ≤ 0 ζij = 0,6; при 0 < gij < D ζij = 1 - 0,4(1 - gij/D)4; при gij ≥ D ζij = 1. |
|||
С.3.5 Прочность сварных швов в случае резки труб со скосом кромки допускается проверять по формуле
N ≤ 0,95AdRwy, (С.12)
где Rwy - расчетное сопротивление сварного стыкового соединения, принимаемое по указаниям 7.4.
С.4 ФЕРМЫ ИЗ ДВУТАВРОВ
С.4.1 Узлы ферм из двутавров с параллельными гранями полок (рисунок С.3) проверяют согласно требованиям С.1, а также учитывают:
несущую способность участка стенки пояса, соответствующего сжатому элементу решетки;
несущую способность поперечного сечения пояса на сдвиг.
С.4.2 В случае одностороннего примыкания к двутавровому поясу двух двутавровых элементов решетки или более с усилиями разных знаков (рисунок С.3, а, б), а также одного элемента в опорных узлах (рисунок С.3, в) при g ≤ 15 мм несущую способность полки пояса проверяют для каждого примыкающего элемента по формуле
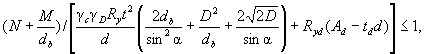 (С.13)
(С.13)
где γD - коэффициент, определяемый по указаниям С.2.2.
С.4.3 Несущую способность участка стенки двутаврового пояса под действием сжатого двутаврового элемента решетки проверяют по формуле
Nsin2α/(1,5γcγDRydbtw) ≤ 1, (С.14)
где tw - толщина стенки пояса.
С.4.4 Несущую способность поперечного сечения двутаврового пояса под воздействием поперечной силы в узле проверяют по формуле
Q/{γcRs[A - (2 - χ)Dt + (tw + 2r)t]} ≤ 1, (С.15)
где Q - поперечная сила в узле, равная меньшему из произведений Nsin α;
Rs - расчетное сопротивление сдвигу стали пояса;
![]()
r - радиус закругления профиля пояса.
С.4.5 Несущую способность двутаврового элемента решетки вблизи примыкания к поясу проверяют по формуле
N(1 + 0,05d/t)/(γcγdRydAd) ≤ 1, (С.16)
где γd - коэффициент, принимаемый по указаниям С.2.2.
С.4.6 Сечения сварных швов, прикрепляющих элементы решетки к поясу, принимают соответственно прочности участков (полок, стенок) двутаврового элемента решетки.
а - K-образный при треугольной решетке; б - то же, при раскосной решетке; в - опорный
Рисунок С.3 - Узлы ферм из двутавров
ПРИЛОЖЕНИЕ Т
(рекомендуемое)
СЖАТЫЕ ЭЛЕМЕНТЫ С ГИБКОЙ СТЕНКОЙ
При расчете центрально- и внецентренно сжатых стержней сплошного сечения
в случаях, когда фактическое значение условной гибкости стенки ![]() превышает (при центральном сжатии не
более чем в 2 раза) значение предельной
условной гибкости стенки
превышает (при центральном сжатии не
более чем в 2 раза) значение предельной
условной гибкости стенки ![]() , полученное согласно
требованиям 8.3.2, 10.4.2, 10.4.3, рекомендуется в формулах (7), (94), (96) при α ≤ 0,5 по 10.4.2, (100), (101), (105) и (106) принимать расчетную уменьшенную площадь сечения Ad взамен A.
, полученное согласно
требованиям 8.3.2, 10.4.2, 10.4.3, рекомендуется в формулах (7), (94), (96) при α ≤ 0,5 по 10.4.2, (100), (101), (105) и (106) принимать расчетную уменьшенную площадь сечения Ad взамен A.
Значение Ad рекомендуется вычислять по формулам:
для двутаврового и швеллерного сечений
Ad = A - (hef - hd)tw; (Т.1)
для коробчатого сечения:
при центральном сжатии
Ad = A - 2(hef - hd)tw - 2(bef,1 - bd)tf; (Т.2)
при внецентренном сжатии
Ad = A - 2(hef - hd)tw. (Т.3)
В формулах (Т.1) - (Т.3) обозначено:
hef и hd - расчетная и уменьшенная высота стенки, расположенной параллельно плоскости, в которой проверяется устойчивость;
bef,1 и bd - расчетная и уменьшенная ширина пояса коробчатого сечения, расположенного перпендикулярно плоскости, в которой проверяется устойчивость.
Значение hd в центрально-сжатых элементах рекомендуется вычислять по формулам:
для двутаврового сечения
где при ![]() рекомендуется
принимать
рекомендуется
принимать ![]() ;
;
для коробчатого сечения
где при ![]() рекомендуется
принимать
рекомендуется
принимать ![]() ;
;
для швеллерного сечения
Для центрально-сжатых элементов значения ![]() и
и ![]() в формулах (Т.4) - (Т.6) рекомендуется принимать согласно требованиям 8.3.2. При вычислении значения hd для
коробчатого сечения по формуле (Т.5)
вместо hd, tw,
в формулах (Т.4) - (Т.6) рекомендуется принимать согласно требованиям 8.3.2. При вычислении значения hd для
коробчатого сечения по формуле (Т.5)
вместо hd, tw, ![]() и
и ![]() рекомендуется принимать соответственно bd, tf,
рекомендуется принимать соответственно bd, tf, ![]() и
и ![]() , при этом значение
, при этом значение ![]() рекомендуется
определять согласно требованиям 8.3.8.
рекомендуется
определять согласно требованиям 8.3.8.
Во внецентренно сжатых элементах двутаврового и коробчатого
сечений значение hd рекомендуется вычислять по формулам соответственно (Т.4) и (Т.5). При этом в этих формулах значения ![]() и
и ![]() , рекомендуется принимать согласно
требованиям 10.4.2.
, рекомендуется принимать согласно
требованиям 10.4.2.
Ключевые слова: стальные строительные конструкции зданий и сооружений, особые условия эксплуатации стальных конструкций, расчетные характеристики материалов и соединений, проектирование стальных конструкций с учетом предотвращения хрупкого разрушения, группы стальных конструкций, методика подбора минимальных сечений изгибаемых элементов
|
|